Теория ошибок

Теория ошибок – дисциплина, которая изучает законы возникновения и распределения ошибок измерений, а также методы их обработки. Виды измерений: 1)полученные непосредственно из измерения (длина линии при изм. мерной летной) и косвенным путем (неприступные расстояния); 2) необходимые (назыв.минимальное кол-во измерений, которое нужно выполнить для определения искомой величины) и избыточные (назыв измерения в которых для контроля всегда выполняются дополнительные измерения) вычисл. по формуле : r=n-k, где n – общее число изм., k – необходим число изм.; 3) равноточные (измерения выполненные одним и тем же инструментом, при одинаковых внешних условиях, по одной и той же методике, наблюдателями одинаковой опытности) и неравноточные (если хотя бы одно из условий равноточности нарушается это приводит к неравноточности).

Ошибки измерений

Теория ошибок делит ошибки на: грубые(возникают при просчетах и промахах, теор.ош. их не изучает), систематические ( назыв ошибки МО которых отлично от нуля. Н.ошибка компарирования), случайные (ошибки измерений которых имеют различные знаки и их МО равно 0). Св-ва случайных ошибок: 1) их МО равно нулю; 2) Положит и отриц ошибки появляются равновозможно; 3) Малые по абсолютной величине ошибки появляются чаще чем большие; 4) Ошибки не превосходят определенной величины равной 3m. Истинная ошибка измерения: Δi=xi-X, где xi – результат измерения, Х – истинное значение измеренной величины. Истинное значение практически никогда не известно.

Средняя квадратическая ошибка

Это МО квадрата истинной ошибки, т.е. нач момент второго порядка: . Истинная ошибка состоит из: Δ=Θ+с; . Т.е. любая СКО содержит случайную и систематическую составляющую. Систематической ошибкой можно пренебречь если ее величина равна: , Θ – случайная ошибка.

Равноточные измерения

Условие: измерения выполненные одним и тем же инструментом, при одинаковых внешних условиях, по одной и той же методике, наблюдателями одинаковой опытности. Т.к. равноточность подразумевает одинаковую точность каждого измерения для хар-ки точности любого одного измерения используют СКО одного измерения. Наиболее надежным значением из ряда равноточных измерений будет среднее арифметическое, которое вычисляется по формуле: , где х – результат измерения, n – число изм.

Оценка точности равноточных измерений

1) СКО одного измерения. Если известна истинная ошибка измерения Δ, которая находиться по формуле: Δi=xi-X, где xi – результат измерения, Х – истинное значение измеренной величины. .СКО одного измерения находим как: а) n>=30. Формула Гаусса: , где ; б) n<30. Формула Бесселя: . 2) При вычислении СКО удерживают две значащих цифры. Для того чтобы убедиться что этого достаточно вычислим СКО самой СКО: - если СКО вычислено по формулам Гаусса, - -«»- по формулам Бесселя; 3) СКО среднего арифметического: вычисляется по формулам: , где m – CКО одного измерения, n – число измерений. 4) Кроме СКО для хар-ки точности равн.измерний используют среднюю и вероятную ошибку: Средняя ошибка - , ν – уклонение ср.кв.значения. Для вычисления вероятной ошибки r, которая хар-ет середину ряда используют или ряд истинных значений Δ, или уклонения от среднего ν. Эти величины берут по абсолютной величине и выстраивают в порядке возвр. Вероятная ошибка r будет равна центральному значению из полученного ряда если число измерений нечетное или среднему из двух центральных знач. при четном числе измерений.

Относительные ошибки измерений Абсолютные

Абсолютными ошибками назыв СКО, среднюю v, вероятную r, истинную Θ. Относительной ошибкой – назыв. величину получаемую как отношение ошибки измерения к результату измерения: m_x/x. В геодезии принято представлять относительную ошибку в виде простой дроби: 1/(х/m_x) И округлять до целых сотых. В зависимости от того какую точечную оценку использовали для хар-ки точности различают относит. истинная ош. – Δ/х, относит ср.кв.ош – ν/х, относит вер-я ош – r/x.

СКО функции. Принцип равного влияния

Если представить ф-ю F(x)=F(x1, x2…xn), которую оцениваем как ф-ю измеренных величин, то СКО ф-ии для некоррелированных измерений будет найдена как: , где - частная производная оцениваемой ф-ии по i-му измерению. Если измерения коллерированы: , m_xi m_xj – коэф.кореляц между i-м j-м измерениями. Для определения СКО отдельных аргументов применяют принцип равного влияния. Суть принципа в том что влияние каждого источника ошибок на конечный результат применяют одинаковым:

1)СКО алгебраической суммы: F=x1±x2±..±xn, - для неравноточных. Частный случай когда измерения равноточны: . В этом случае формула приобретает вид:

2)Как СКО ф-ии получают и СКО арифметической середины: ,

Неравноточные измерения

Неравноточными назыв измерения в которых каждое измерение будет иметь свою отличную от других СКО. Вычислить ошибку каждого неравноточного измерения сложно, поэтому для хар-ки неравноточ измерений применяют относительную меру точности, которую назыв.весом. Веса измерений обратны квадратам СКО: , mi – ско соотв измерения, с – произвольная постоянная для данного ряда измерений. При выборе с стараются чтобы вычисленные веса измерений были близки к 1.Зная вес всегда можно определить величину СКО измерения: . При оценке точности заменяют с=μ².

Ошибка единицы веса для ряда неравноточных измерений играет ту же роль что и СКО одного измерения для ряда равноточных: . Для вычисления ошибки единицы веса используют формулу Гаусса: - когда известно истинное значение, - при n<30, - при n>30.

Наиболее надежное значение из ряда неравноточных измерений и его оценка точности:

Наиболее надежным будет ср.весовое . Эту величину так же назыв.общая арифметич.середина. СКО среднего весового: .

Вес функции:

Формулы для вычисления весов ф-ии получают из формул для вычисления весов ф-ий разделив их на μ².

Для некоррелированных измерений: . Для коррелированных:

Задача уравнивания

Наличие в сети избыточных измерений приводит к неоднозначности определения неизвестных, а значит возникает задача ур-я, которая Состоит в определении наиболее надежных значений неизвестных параметров и их оценки точности. Мы решали такую задачу при обработке измерения одной величины в теории ошибок. Принципиальное отличие задачи в том что в обработку включаются разнородные величины. Существует два вида ур-я: параметрический и корелантный.

Параметрический способ ур-я

Х – истинное значение неизвестного параметра, У – истинное значение измеренной величины, у – измеренное значение. Результаты измерений всегда можно связать с какой то ф-ей. Т.к. в общем случае ур-е (1) нелинейно приведем его у линейному виду разложив в ряд Тейлора

Порядок уравнивания параметрическим способом

1) Выберем неизвестные и обозначим их xj. 2)Составим у-е связей между измеренными значениями и неизвестными У=φ(х). 3) Составим параметрическое у-е поправок А∆х+L=V. 4)Находим приближенное значение неизвестных и вычисляем свободные члены параметрических у-ий поправок: φ(х⁽⁰⁾)-у=L. 5) Составим нормальное у-е R∆x+B=0, R=A^TA, b=A^TL. 6) Получим поправки из уравнивания приближенным значением неизвестных ∆х=-R^-1b. 7) Вычислим уравненные значения неизвестных . 8) Выполним оценку точности.

Запись матричных выражений в параметрич.способе

Параметрич.у-е поправок

V=A∆x+L

Для каждого измерения

Матрица поправок изм.знач.

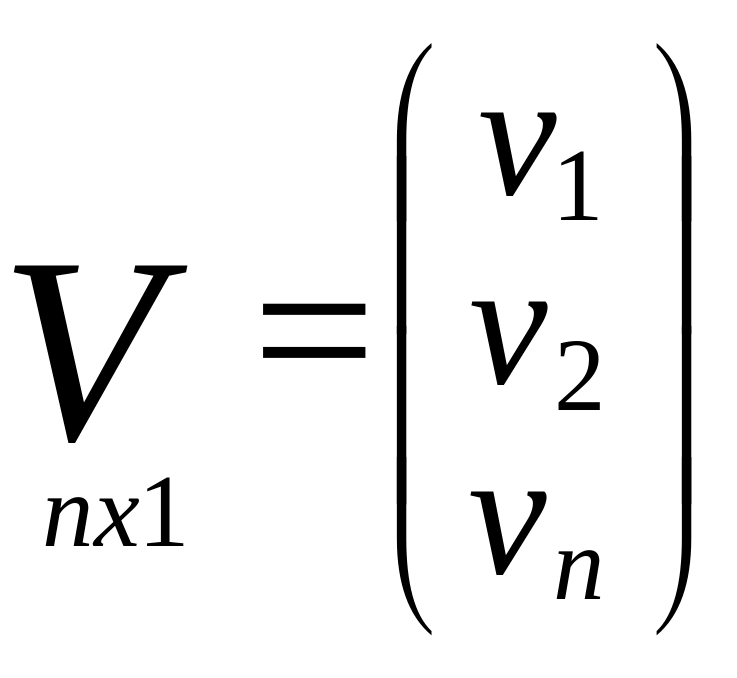
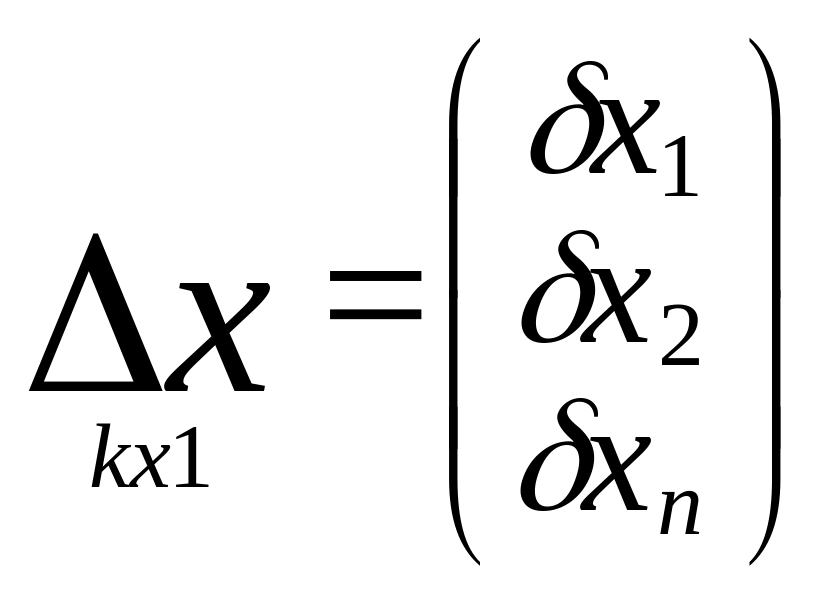
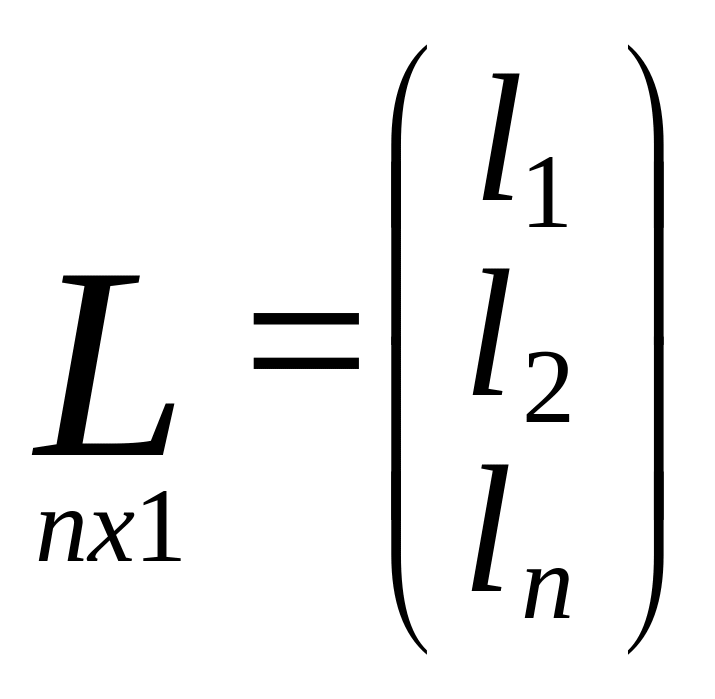
Матрица частных произв.

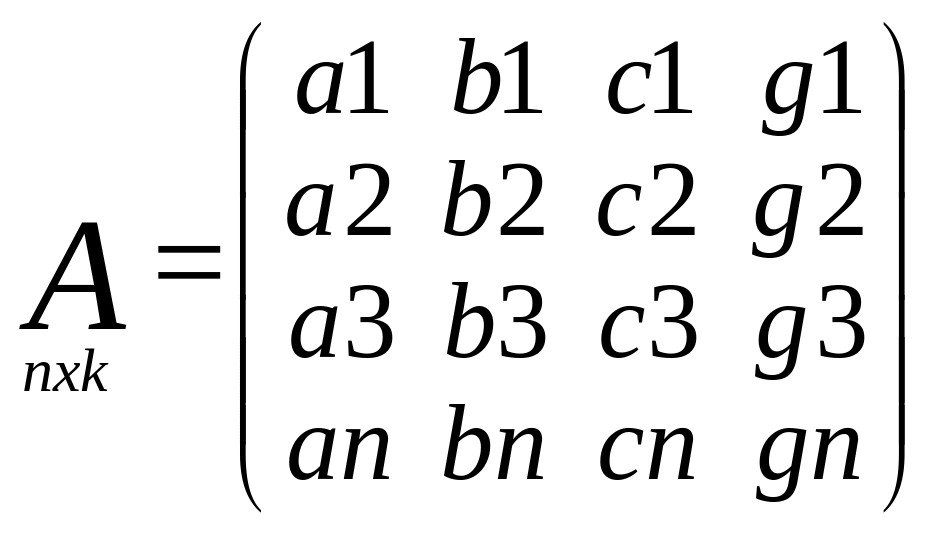
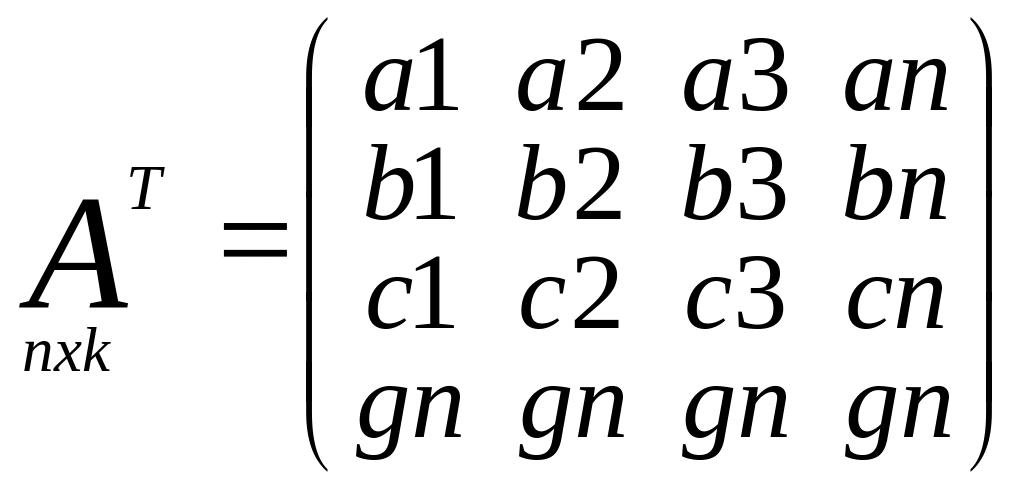
Матрица коэфиц. норм.ур-й. Св-ва: 1) по диагонали стоят квадратичные коэф., они всегда положит. 2) не лиагональные элементы симметричны относительно главной диагонали.

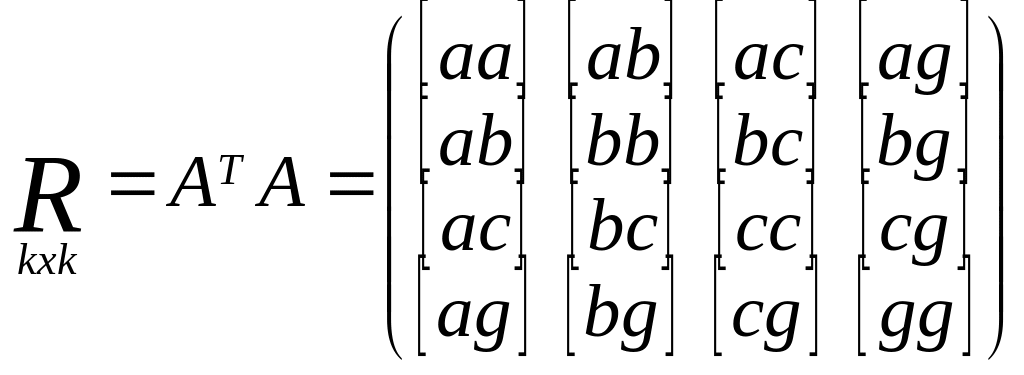
Матрица свободных членов нормальных ур-ий

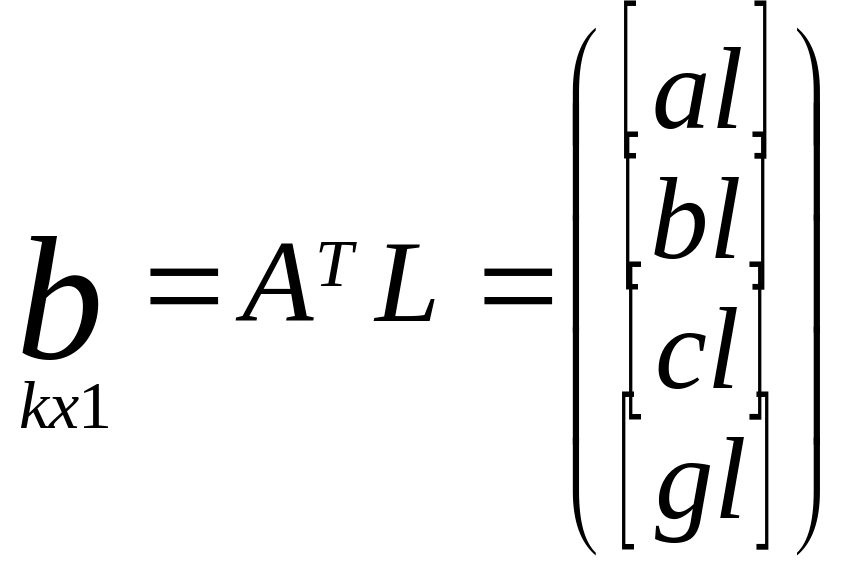
Номальные у-я для 4 неизвестных

R∆х+b=0

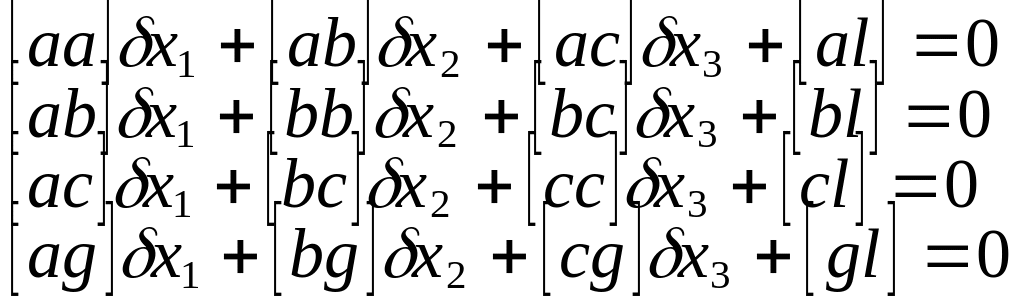
Способы решения нормальных ур-ий

Прямой способ, когда решения получают в виде: ax=b, x=b/a. При прямых способах мы можем заранее указать кол-во операций. Приближенный способ, когда решения получаем в виде: ax+x-x-b=0, xⁱ=(1-a)x^i-1-b, т.е. в каждом последующем приближении I используется значение неизвестного x^i-1 полученное в предыдущем приближении. В этом способе мы заранее не можем описать кол-во операций, но этот способ занимает меньше памяти в ЭВМ.

Оценка точности при параметрическом способе

а) оценка точности неизвестных. Обратный вес уравненного значения каждого неизвестного будет равен соотв.диагональному элементу обратной матрицы коэф.норм. ур-й .В матрице Q по диагонали стоят обратные веса неизвестных ее так же назыв. весовой матрицей.

б) вычисление ошибки единицы веса. При параметр. способе ошибки единицы веса вычисляются по формуле: , здесь v может быть вычислено по формуле: , где n – общее число изм., k – число необходим изм., равное числу определяемых неизвестных.

Ур-ие неравноточных измерений

1)пусть измерения неравноточны, чтобы привести их к равноточному виду мы умножим их на матрицу:

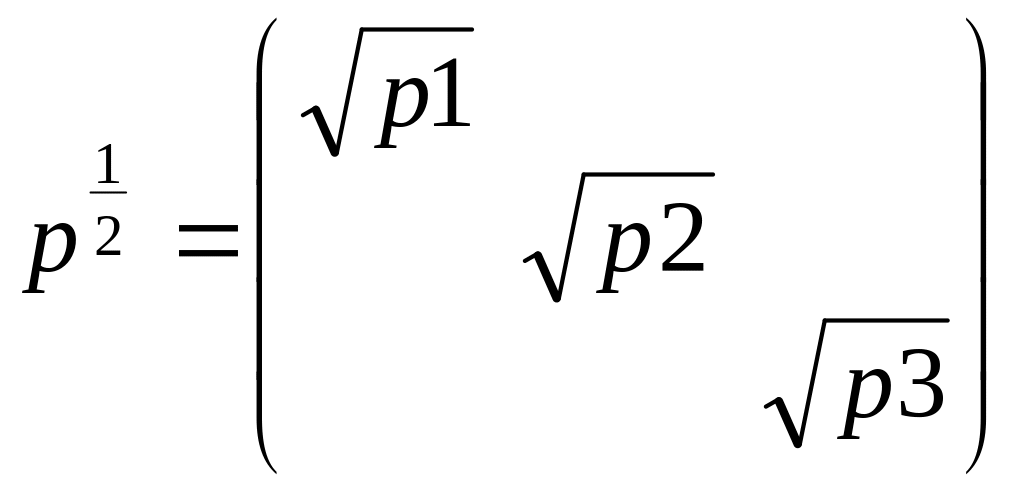
. Получим у-е: . Решаем задачу также как и для равноточных изм.: получим нормальное у-е и вектор решения: ; . Из ур-я мы получим , чтобы получить величину V. После ур-я разделим поправки:

2) для учета неравноточных измерений во все алгоритмы Гаусса ввести веса измерений и получит алгоритмы в виде: ;

Коррелатный способ ур-я

Сущность ур-я коррелатным способом заключается в том чт задачу нахождения минимума ф-ии зависимых переменных [pv2] решают способом Лагранжа, вводя вспомогательные множители независимых условных ур-ий. Приводит к тем же результатам что и параметрический, но иногда более выгоден.

Порядок ур-я корелатным способом

1) Подсчитываем число избыточных измерений в геод.сети. Каждое избыточное измерение приводит к возникновению независимого ксловного у-я поправок. 2) Составляем у-е связей между измеренными величинами которые выражают какое-то математическое соотношение: φ(У)=0; 3) Составляем условное у-е поправок: BV+w=0; 4) Составляем нормальные у-я: Nk+w=0; 5)Получаем корелаты решив у-е любым известным споcобом: k=-N^-1w; 6) вычисляем поправки к измеренным величинам: V=p^-1B^Tk; 7)Вычисляем уравненные значения измеренных величин ; 8) По уравненным значениям измерений вычисляем значения неизвестных; 9) Оценка точности.

Подробная запись матричных выражений

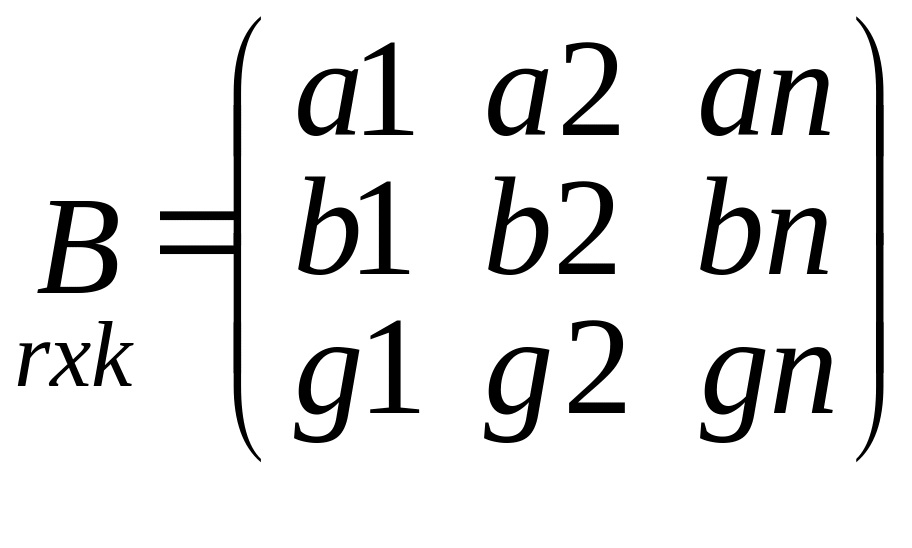
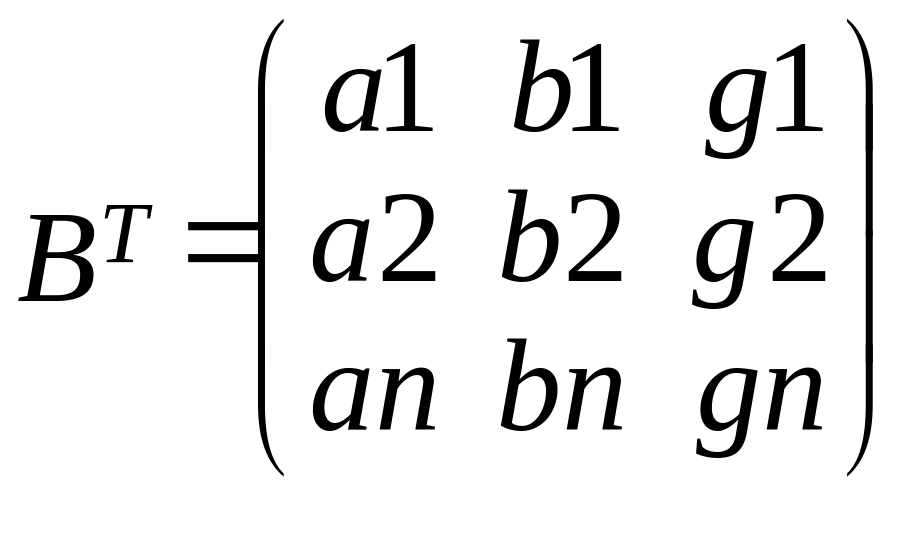
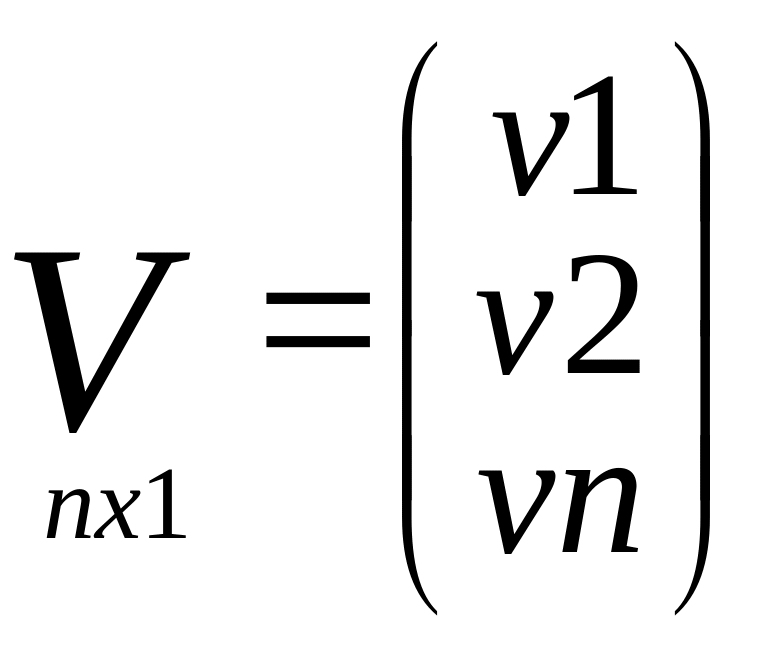
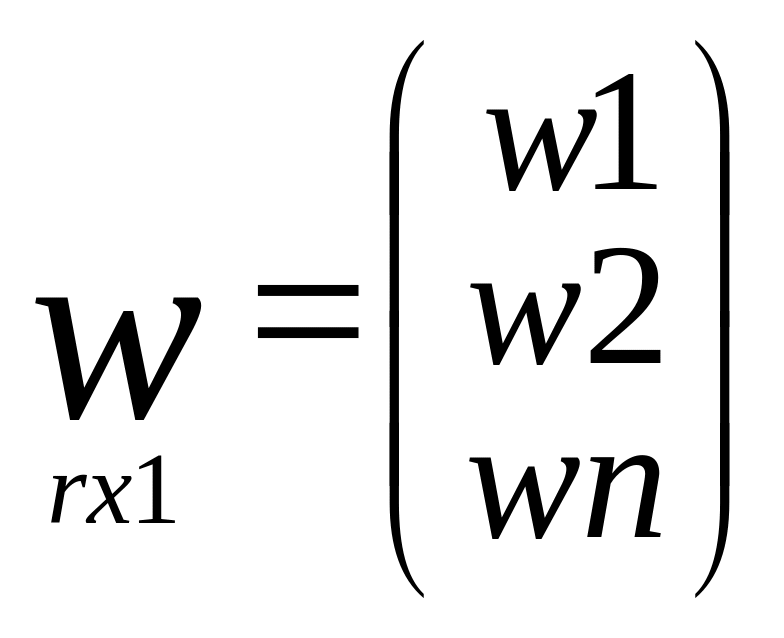
C учетом у-я поправок:

Нормальные у-я в подробной записи:

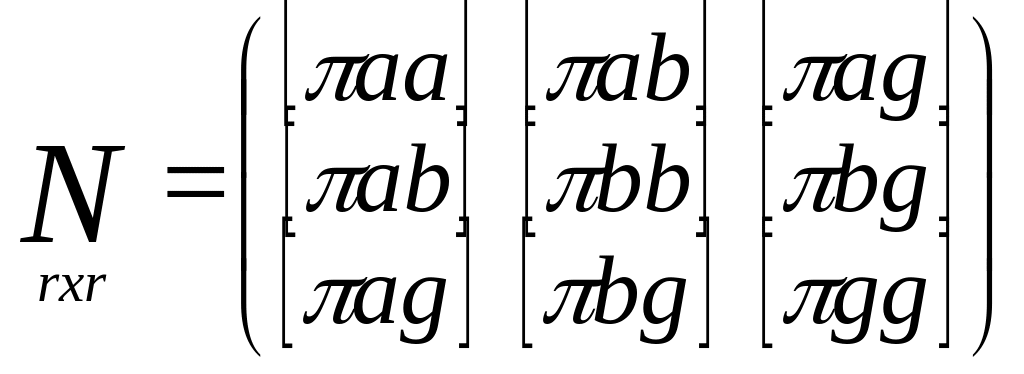, где - обратный вес

Порядок обработки ряда неравноточных измерений

1) Вычисляем общую арифметич. середину: , где ε_i=x_i-x’, x’=minx_i . 2) Вычисялем уклонения v_i=х_о-х_точн и выполняем контроль , где ошибка округления при вычислении будет . 3)Вычисляем [pv²] с контролем: . 4) Вычисляем μ, M, m_μ, m_{M b} и строим доверительные интервалы

Порядок обработки ряда равноточных измерений

1.Вычисляем простую арифметич. середину: , где ε_i=x_i-x’, x’- приближенное значение х (обычно минимальное значение x_i). 2) Вычисляем отклонения v_i= х_i-x_окр, и выполняем контроль , где β – ошиюка округления х - . 3) Вычисляем [v²] с контролем: . 4) Вычисляем m, M, m_m. 5)Cтроим доверительные интервалы ; ;

Число нормальных ур-й в параметрическом и корелатном способе

В параметрическом способе: это определенная система из k линейных уравнений с k неизвестными: R∆х+b=0. В корелатном: в системе нормальных уравнений число уравнений r равно числу неизвестных.

Алгоритм гаусса. Эквивалентные ур-я.

Система эквивалентных у-й имеет вид:

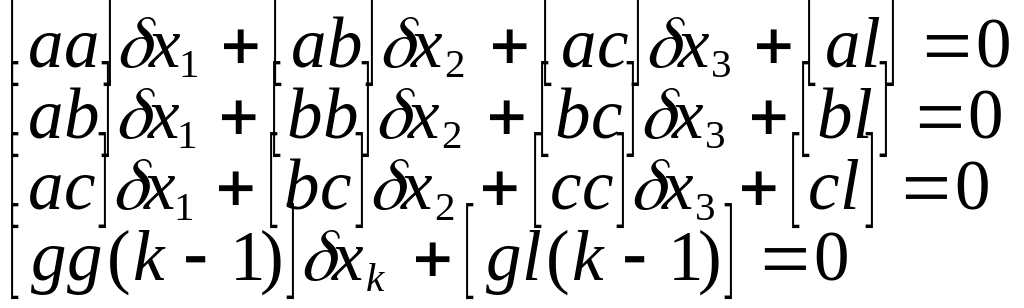
Алгоритм полученный для вычисления коэффициентов в экквивалентной системе, назыв алгоритмом Гаусса. Первый сомножитель получается как произведение первой буквы знаменателя на первую букву раскрываемого алгоритма, а второй как произведение второй буквы знаменателя на его вторую букву