Сравнение эмпирического распределения с нормальным:

Для сравнения эмпирического распределения с нормальным: используют несколько критериев: приближенные, ассиметрия и эксцесс, критерий χ². Приближенный критерий: в случае нормального распределения между средним v и вероятным r и средним квадратическим отклонением σ существует зависимость: . Асимметрия и эксцесс: для нормального закона распределения скошеность Sk и эксцесс Е кривой распрделения равны 0. НА практике если выполняется условие принимают гипотезу про нормальное распределение эмпирического ряда. Критерий χ² В критерии используются сравнения количественных значений, которые попали в интервал k_j и количество значений, которые попали бы в интервал в случае нормального закона распределения np_j. Значение критерия находят по формуле

Статистическая проверка гипотез

Эта задача возникает когда необходимо проверить соответствие опытных данных каким-то вероятностным суждением, по значениях или поведении исследуемых СВ. (напр. в геодезии статистич. проверку гипотез выполняют при сравнении эмпир.измерений с теоретическими). Для проверки связи выбирают какую-либо статистич.характеристику значение которой можно определить и при сделанных вероятностных предположениях, а ее величину и для статистических данных. Такие статистич.хар-ки назыв. критерием проверки. Для выбранного критерия определяют область критических значений и соотв. ей области значимости α. Значение α обычно выбирают 1,2,5, 10%. Уровень значимости опред.вероятность попадания критерия в область критических значений, если гипотеза верна. Дополнительно к ней выбирают область допустимых значений. Если значение критерия вычисленного по статистич. данным попадает в критич.област гипотезу отвергают. Если в область доп.значений, то говорят что значения критерия не противоречат гипотезе и ее можно принять пока она не будет опровержена дополнительными исследованиями. При статистич проверке можно совершить ошибку 1го рода, отвергнуть гипотезу если она верна, или ошибку 2го рода, принять не верную гипотезу. Чтобы не допустить ошибки 2го рода необходимо уменьшить область допустимых значений, при этом сразу возрастает вероятность ошибки 1го рода, ставиться задача выбрать область допустимых значений т.о.чтобы вероятность попадания в нее критерия , если гипотеза верна, была максимальна. Эту вероятность назыв. мощностью критериев.

Оценивание параметров распределения

Например: обозначим неизвестное значение параметра через: a_s s[1;t]. Для нормального закона распределения их будет 2 а₁=а, а₂=σ. Для точных но неизвестных параметров, по результатам выборок находим оценки a_s^* которые будут являться функциями от выборки: a_s^*= a_s (х1, х2,…,хn). Причем эти оценки должны быть максимально близки к значениям параметров, которые мы определяем. Для этого оценки должны обладать след. св-ми: 1) состоятельность – вер. предел оценки должен стремится к неизвестному параметру (lima_s^*=a_s);

2) несмещенность – МО оценки должно явл. неизвестному параметру . Т.е. в оценках не должно быть систематич.ошибки ( М_as*= a_s); 3) эффективность – дисперсия ошибки должна быть минимальной. Оценки обладающие этими свойствами назыв. доброкачественными (D_as*=min).

Методы определения оценок

1) Метод моментов. В этом методе при нахождении оценок МО заменяется ср.арифметическим:

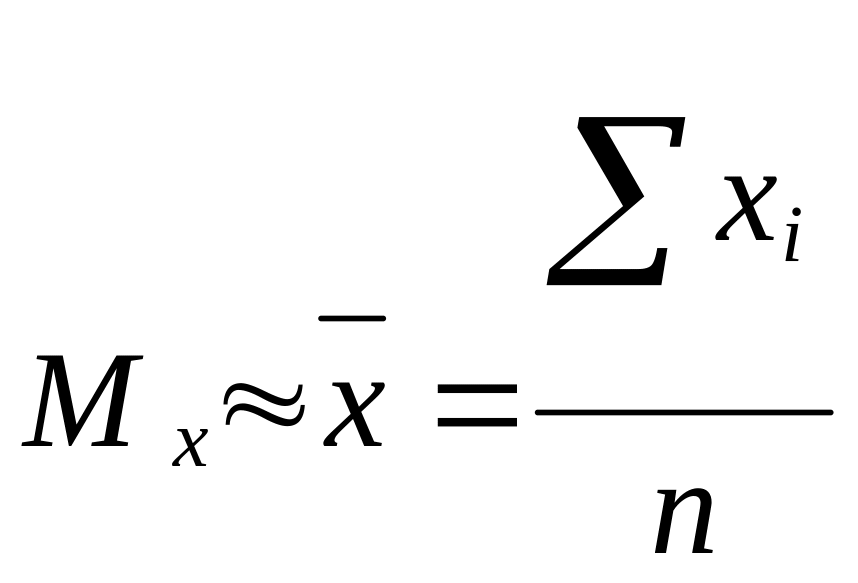
. Но этот метод не всегда позволяет получить доброкачественные оценки.

2) Метод максимального правдоподобия. Составл. ф-ю правдоподобия Li, каждое i-е измерение рассматрив. как постоянные, а неизвестные параметры как переменные. Затем составляем ф-ю макс. правдоподобия: Li=φ(xi, a1, a2…at). Значение оценок для неизвестных параметров находим как . Оценки не изменяются, а вычисления облегчаются, если предварительно ф-ю макс.подобия прологарифмировать.

3)Метод наименьших квадратов.

Доверительное оценивание

Все оценки найденные по рассмотренным методам опред ошибок будут точечными, при небольшом числе наблюдений значение ошибки может значительно отличаться от неизвестного параметра, кроме этого мы не знаем с какой вероятностью получено значение точечной оценки. Более надежными будут интервальные оценки: . Т.е. значение неизвестного параметра с заданной вероятностью находиться внутри некоторого интервала.

Доверитетельным – назыв. интервал с фиксированными концами, которые с заданной доверит.вероятностью, накрывает значение неизвестного параметра. Значение неизвестного параметра равновозможно может находиться в любой точке доверительного интервала. Бывают симметричными: пример интервал для МО , где σ*-ср.кв.отклонение для ср.арифметического, х – ср.арифметич., tβ –коэф.зависящий от выбранной доверительной вероятности β.И ассиметричными: пример довер.интервал для ср.кв.отклонения: , где коэф. γ1, γ2 – находят из таблиц, они зависят от доверит.вероятности и числа степеней свободы r.