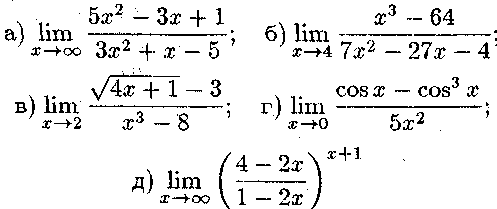2. Приклади

ПРИКЛАД і. Знайти область визначення функції

2. ПРИКЛАДИ 33

Розв'язок.

Логарифмічна функція визначена, якщо Корені квадратного тричлена: х₁ = —4, Х₂ = 1. Записана вище нерівність рівносильна нерівності —(х + 4)( х — 1) > 0, що можливо

при — 4 < х < 1. Область визначення заданої функції — інтервал (—4; 1).

ПРИКЛАД 2. Знайти границі функцій, не користуючись пра­вилом Лопіталя:

34 2. ТЕМА №2

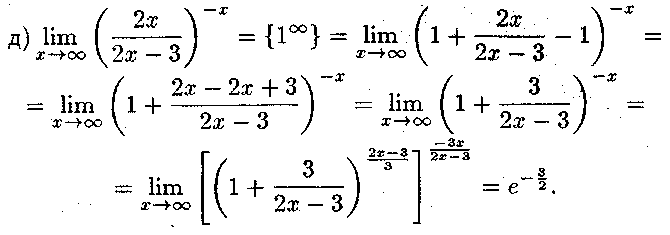
ПРИКЛАД 3. Дослідити задану функцію на неперервність і побудувати її графік

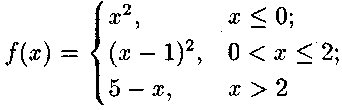
Розв'язок.

. Функціявизначена та неперервна на інтер-

валах, де вона задана неперервними

елементарними функціями. Отже, розрив можливий тільки в точках х₁ = 0, х₂ = 2. Для точки х₁ = 0 маємо:

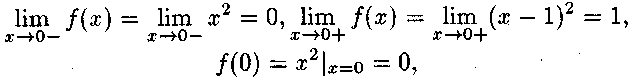
тобто функціяв точцімає розрив першого роду.

Для точки= 2 знаходимо

тобто в точці хі = 2 функція має розрив першого роду. Графік даної функції зображено на рис 2.1.

ПРИКЛАД 4. Знайти похіднідля функцій, заданих в пун­ктах а), б), в), і похіднудля функції, заданої в пункті

2. приклади 35

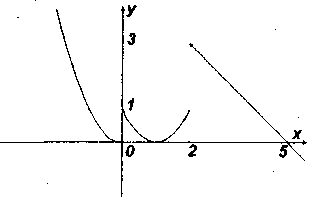
Рисунок 2.1

б) Прологарифмуємо задану функціюі продиференціюємо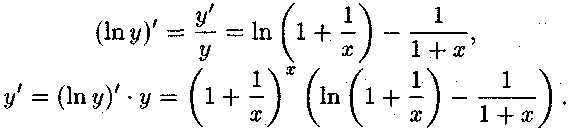одержане рівняння

в) Диференціюючи по х тотожність, одержимотобто

г) Функція на вказаному проміжку строго мо­- нотонно спадає. Тому існує однозначна обернена функція

36 2. ТЕМА №2

Далі, перетворюється в нуль тільки в точках вигляду Тому, якщо то

ПРИКЛАД 5. Знайти границі функцій за правилом Лопіталя:

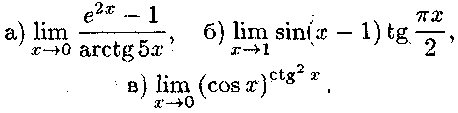
Розв'язок.

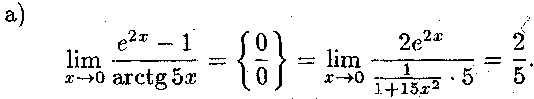
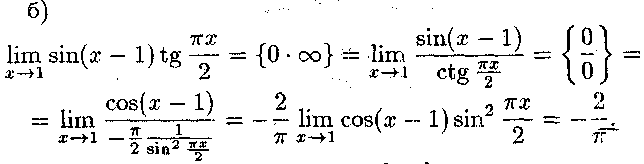
в) Маємо невизначеність типу. Введемо позначен­ня Тодіє невизначеністю типу. Представимо виразу вигляді, зна­йдемо за правилом Лопіталя

Отже,

2. Приклади 37

ПРИКЛАД 6. Дослідити методами диференціального числе­ння функцію і побудувати її графік

1. Областю визначення функції є множина всіх дійс-­ них чисел, крім х = 1, при якому перетворюється в нуль знаменник.

2.Оскільки рівняння х² — 5 = 0 має корені то графік функції перетинає з вісь в точках та. Крім того графік перетинає вісь

в точці

3. Дослідимо існування асимптот. Оскільки приприто пряма х = 3 є вертикальною асимптотою графіка функції.

Із існування границь

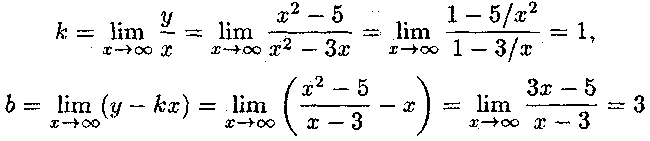
випливає, що графік функції має похилу асимптоту (і ліву, і праву) у = х + 3.

4. Знайдемо похідні

та критичні точки

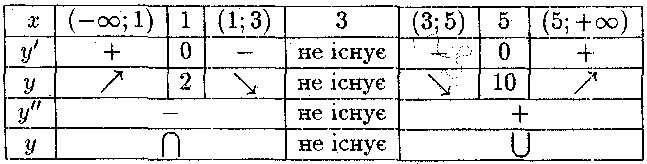
Складемо таблицю зміни знаків першої та другої похідних в залежності від зміни аргументу, включивши в неї критичні точки:

38 2. ТЕМА №2

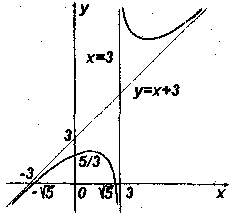
Рисунок 2.2

Графік функції зображено на рис. 2.2

3. Завдання теми 2 Задача № 1.

Знайти області визначення функцій

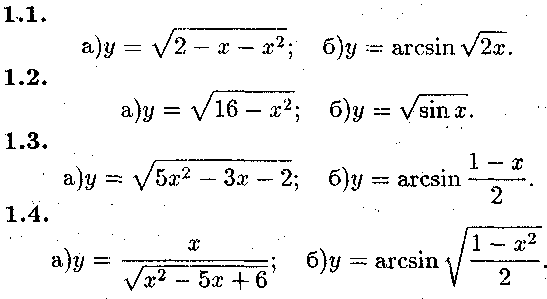
3. ЗАВДАННЯ ТЕМИ 2 39

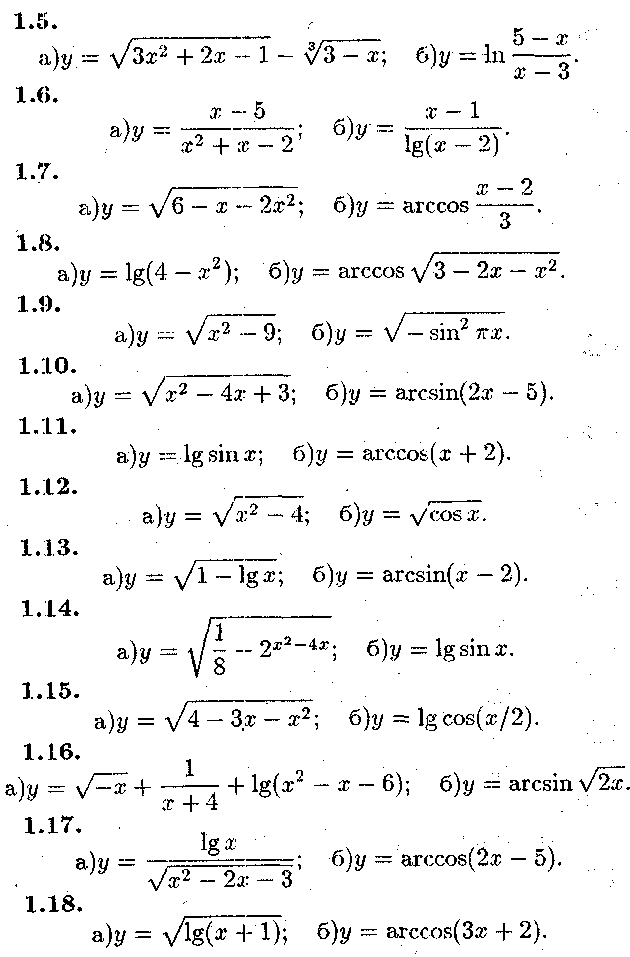
40 2. ТЕМА №2

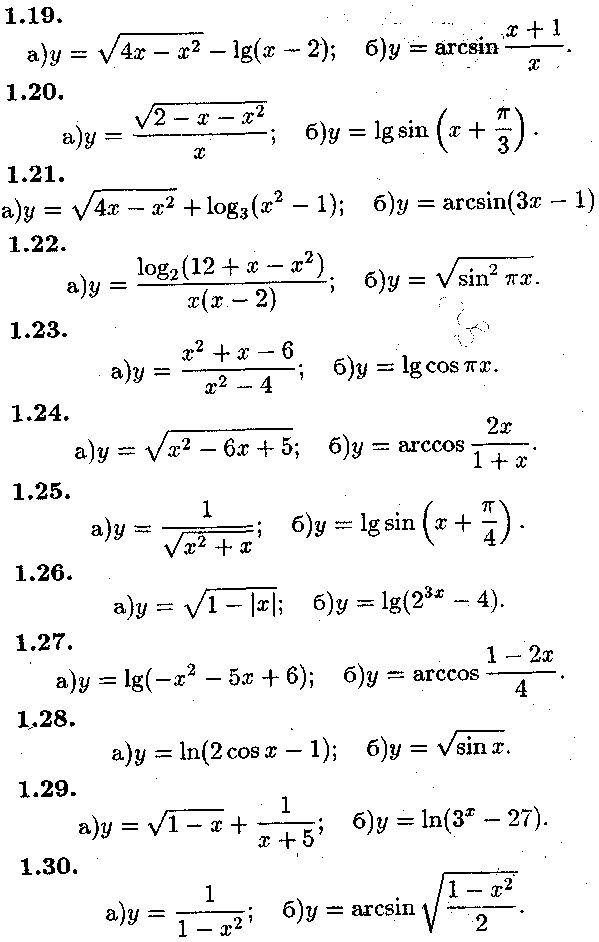
3. ЗАВДАННЯ ТЕМИ 2 41

Задача № 2.

Знайти границі функцій, не користуючись правилом Ло-піталя:

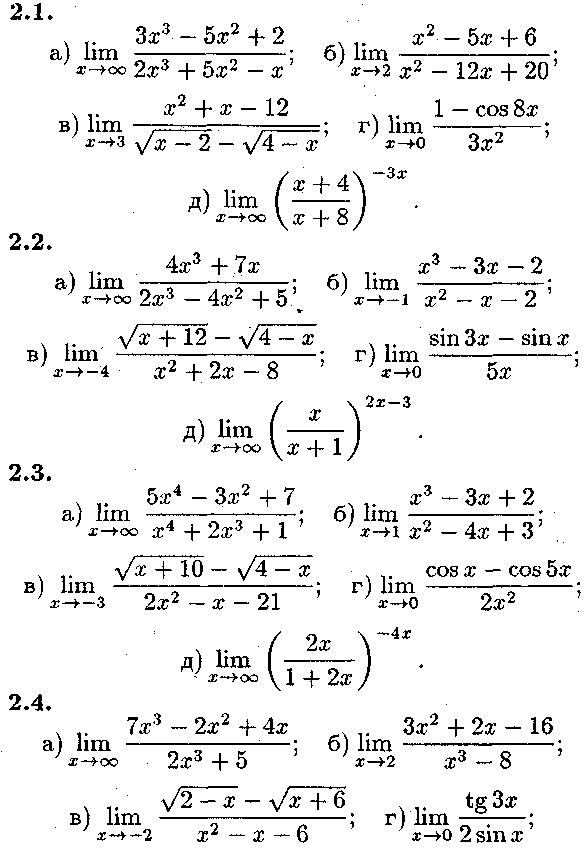
42 2. ТЕМА №2

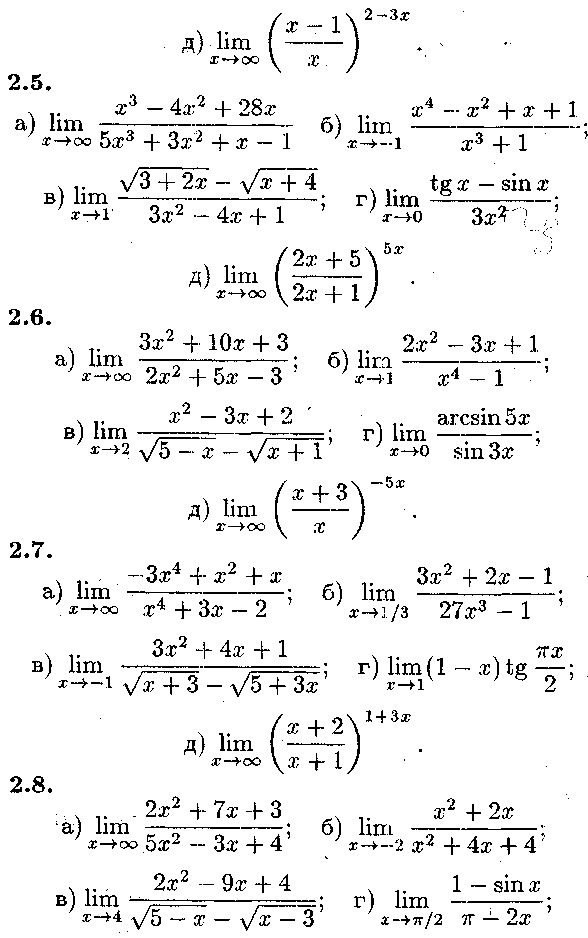
3. Завдання теми 2 43

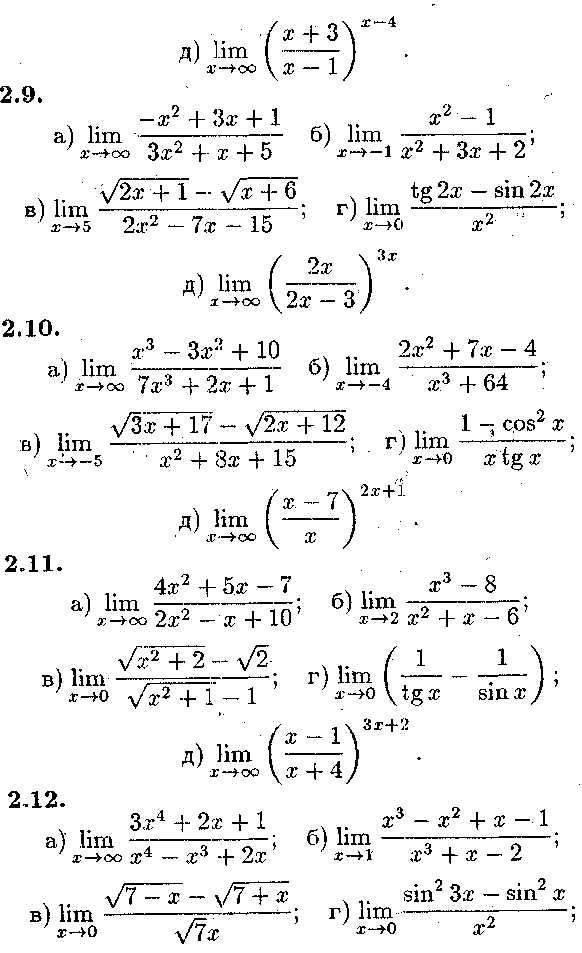
44 2. ТЕМА №2

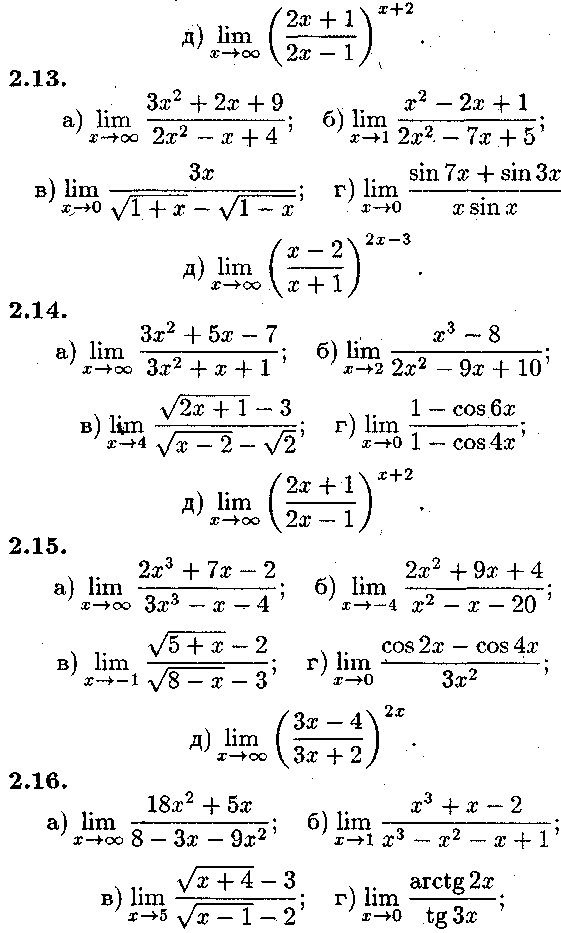
3. ЗАВДАННЯ ТЕМИ 2 45

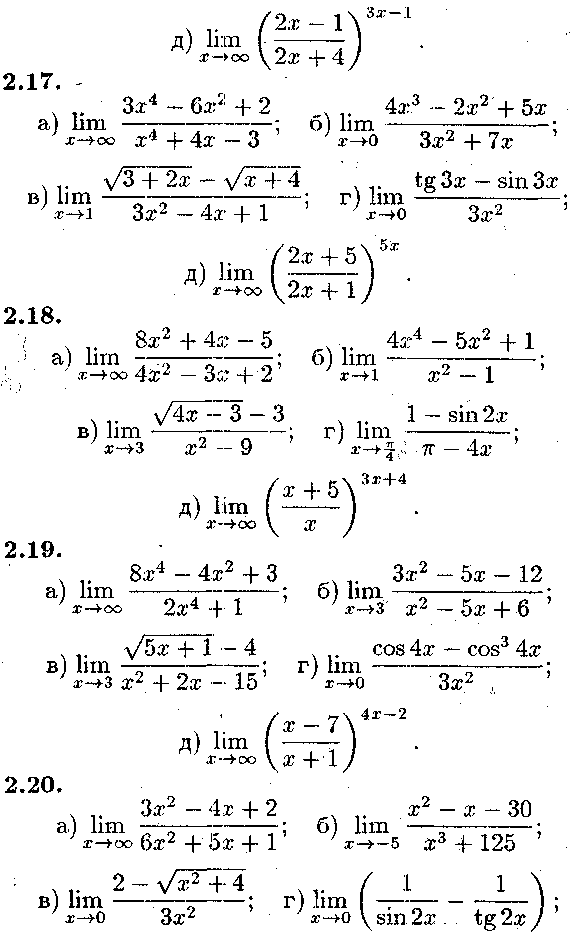
46. ТЕМА №2

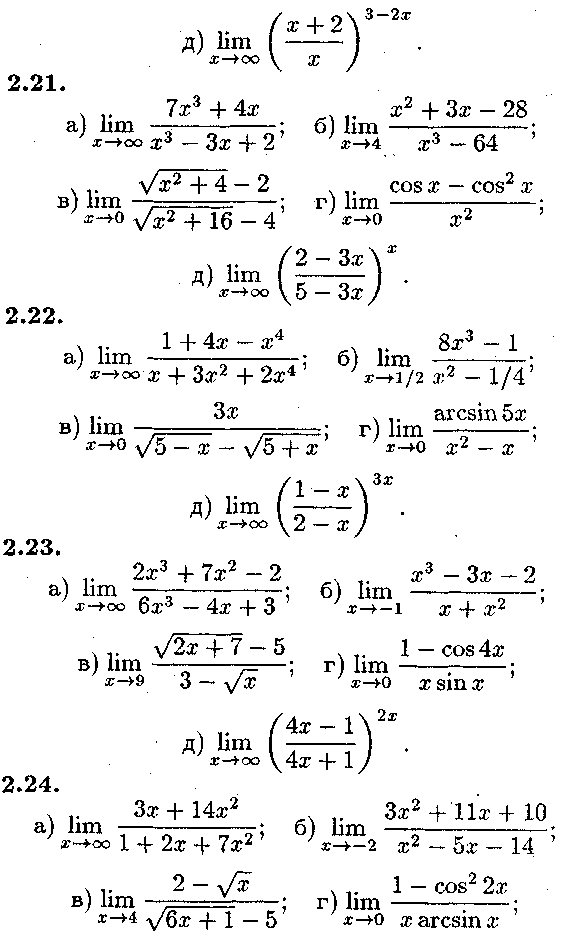
3. ЗАВДАННЯ ТЕМИ 2 47

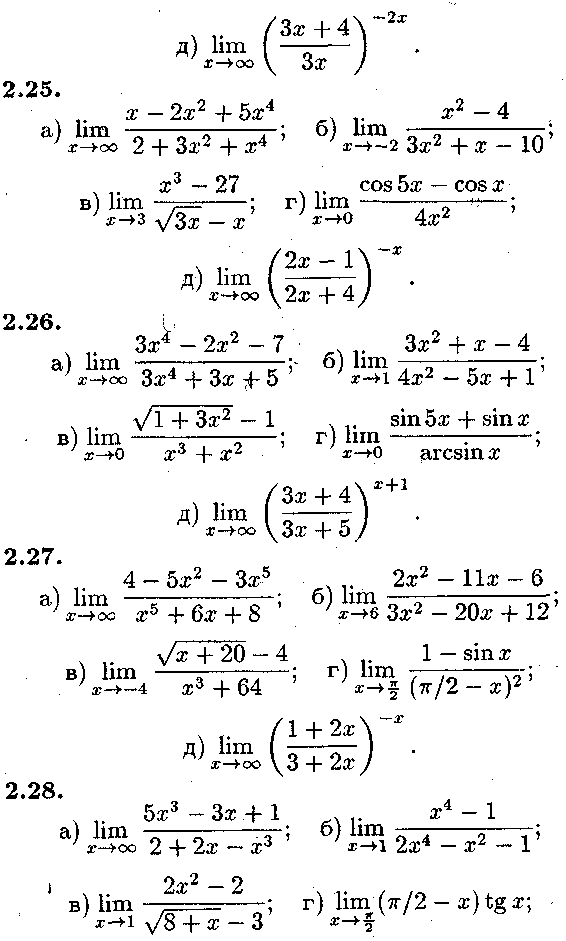
48 2. ТЕМА №2

2.29-

2.30.