Задача № 5.

В пункті а) обчислити поверхневий інтеграл першого роду по поверхні S, де S — частина площини (р), яка відти­нається координатними площинами; в пункті б) обчислити поверхневий інтеграл другого роду.

-

^-частина поверхні параболоїда

(нормальний векторякої утворює гострий кут з ортом), яка відтинається площиною х = 0. 5.2.

122 5- ТЕМА №5

, де S - зовнішня сторона поверхні еліпсоїда..

5.3.

- зовнішня сторона

поверхні куба, обмеженого площинами х= 0, у = 0, z = 0, х = 1, у = 1, z = 1.

5.4.

-зовнішня сторона поверхні сфери

5.5.

верхня сторона

площини х + у + z = 4, яка відтинається координатними площинами.

5.6.

зовнішня сторона

сфери х² + у² + z ² = 16, яка лежить в першому октанті. 5.7.

- зовнішня сторона сфери.

5.8.

- верхня частина

площини х + у + z = 1, що відтинається координатними площинами.

3. ЗАВДАННЯ ТЕМИ 5 123

5.9.

- зовнішня повер­хня циліндра , яка відтинається координатними площинами z =.0, z = 5. 5.10.

- частина по­верхні параболоїда (нормальний векторякої утворює тупий кут з ортом, яка вирізається циліндром

5.11.

- зовнішня сторона нижньої

половини сфери 5.12.

- частина поверхні конуса

, (нормальний векторякої утворює тупий

; кут з ортом, яка лежить між площинами z = 0, z = 1.

5.13.

частина поверхні параболоїда

z =х² + у² (нормальний векторякої утворює тупий кут з ортом'), яка відтинається площиною z= 2.

5.14.,

124 5. ТЕМА №5

— частина поверхні гіперболоїда

(нормальний векторякої утворює тупий кут з ортом), яка відтинається площинами 5.15.

- зовнішня сторона сферияка лежить в першому октанті.

частина поверхні парабо­лоїда z = х² + у² (нормальний векторякої утворює тупий кут з ортом), яка відтинається площиною z = 4.

5.17. ;

— частина поверхні

конуса z² = х² + у², (нормальний вектор якої утворює го­стрий кут з ортом , яка відтинається площинами z = 0,

z = 3.

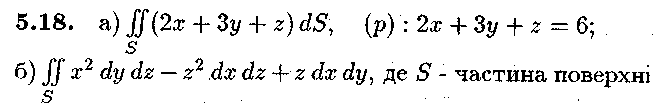
параболоїда z = 3-х² —у²(нормальний вектор якої утво­рює гострий кут з ортом , яка відтинається площиною

z = 0.

5.19.

- частина поверхні конуса х² + z² = у² (нормальний векторякої утворює

3. ЗАВДАННЯ ТЕМИ 5 125

тупий кут з ортом), яка відтинається площинами у = 0, у = 1

5.20.

частина поверхні

параболоїда z = х² + у² (нормальний векторякої утворює гострий кут з ортом), яка відтинається площиною z = 1.

5.21.

- внутрішня сторона циліндра х² + у² = 4, яка відтинається площинами z = 0. z = 1.

5.22. зовнішня сторона

замкнутої поверхні, утвореної параболоїдом 3z = х² + у² і

півсферою

5.23.;

'

- зовнішня сторона

сфери

5.24.

І •■■■--„

- зовнішня сторона

циліндрах² + у¹ = 1, яка відтинається площинами z =0, z =2

5.25

126 5. ТЕМА №5

- частина поверхні

параболоїда(нормальний векторякої утво-

рює гострий кут з ортом),. яка відтинається площиною z = 0.

внутрішня сторона замкнутої поверхні, утвореної конусом

І ПЛОЩИНОЮ X = 1.

5.27.

частина повер­хні параболоїда(нормальний векторякої утворює гострий кут з ортом), яка відтинається площи­ною z = 0. 5.28.

частина

поверхні конуса(нормальний вектор якої

утворює тупий кут з ортом), яка відтинається площина­ми z = 0, z = 4.

5.29. І

- частина поверхні

параболоїда(нормальний вектор " якої

утворює гострий кут з ортом), яка відтинається площи­ною z = 0. 5.30.

3. ЗАВДАННЯ ТЕМИ 5 127

- частина

поверхні конуса(нормальний вектор якої

утворює тупий кут з ортом ), яка відтинається площина­ми у = 0, у= 1.

Задача № 6.

Задано векторне полеі площину

Ax + By+Cz + D = 0 (р), яка разом з координатними площи­нами утворює піраміду. Нехай— основа піраміди, яка належить площині (р);— контур, який обмежує;— зовнішня нормаль до. Обчислити: а) циркуляцію вектор­ного полявздовж замкненого контура, застосувавши формулу Стокса до контураі обмеженої ним поверхні S з нормаллю; б) потік векторного полячерез повну поверхню піраміди V в напрямі зовнішньої нормалі до її по­верхні, застосувавши формулу Остроградського.

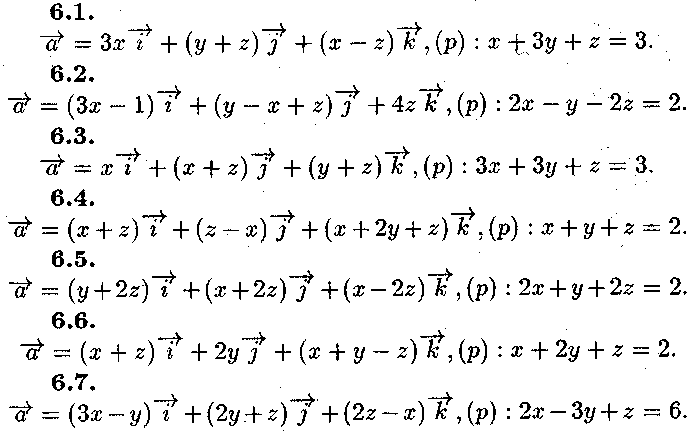
128 5. ТЕМА №5

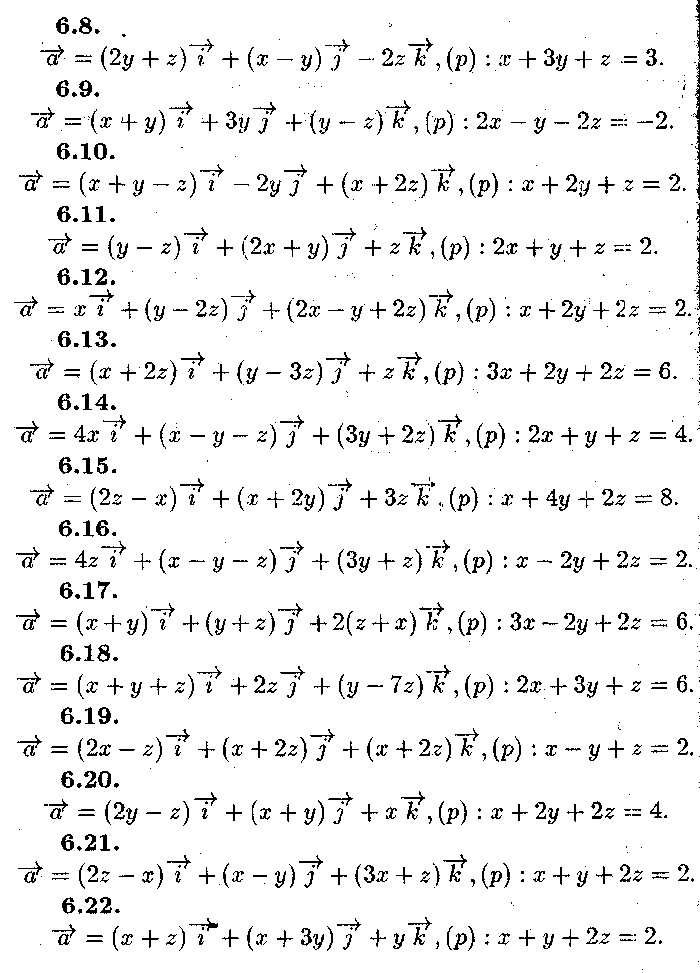
3. ЗАВДАННЯ ТЕМИ 5 129

ТЕМА № 6

Ряди

Література: [1]Кн.2; [2]Ч.2; [3]Ч.2; [4]; [5]Кн.2; [10].