1.4. Полярный график

Для создания полярного графика необходимо нажать кнопку Polar Plot (Полярный график) на палитре Graph (Графики) и поместить в местозаполнители имена переменных и функций, которые будут нарисованы в полярной системе координат (рис. 10).

Сохраните изменения в текущем документе.

1.5. Построение нескольких рядов данных

На одном графике можно отложить до 16 различных зависимостей. Чтобы построить на графике две (и более) кривые, необходимо выполнить следующие действия:

1. Построить график первой кривой (рис.11).

2. Поместите маркер ввода таким образом, чтобы целиком выделить надпись по координатной оси y и введите запятую.

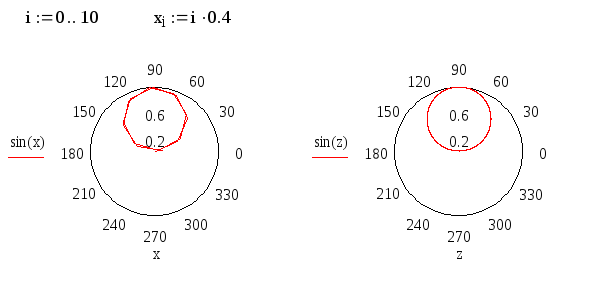
Рис. 10. Полярный график двух векторов и быстрое построение графика

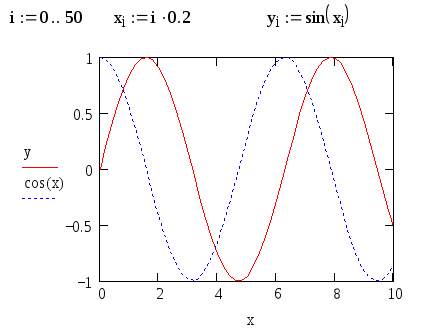
Рис. 11. Построение нескольких зависимостей на одном графике

3. В появившийся местозаполнитель введите выражение для второй кривой, например: cos(x).

Этим способом может быть создано несколько зависимостей, относящихся к одному аргументу. Вместе с тем имеется возможность отображения на одном и том же графике зависимостей разных аргументов.

Реализуйте графики зависимостей, приведенные на рис.12.

Второй график здесь представляет параметрическую зависимость cos(sin(x_i)).

При построении на одном и том же графике нескольких зависимостей разного аргумента достаточно позаботится только о соответствии типа данных для каждой пары точек в отдельности. Например, вполне можно совместно отобразить график функции от ранжированной переменной и график функции, созданной в режиме быстрого построения (рис.13).

Сохраните изменения в текущем документе.

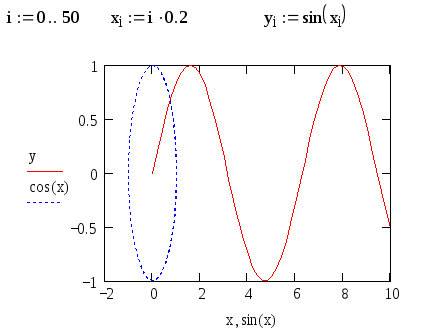
Рис. 12. Построение нескольких зависимостей от разного аргумента

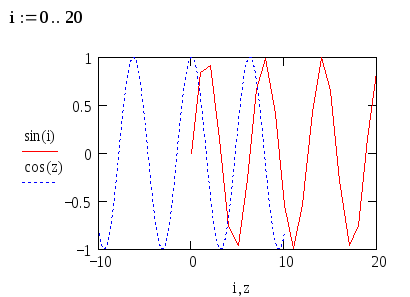
Рис. 13. Построение зависимостей от разного аргумента разного типа данных

1.6. Форматирование осей

Возможности форматирования координатных осей графиков включают в себя управление их внешним видом, диапазоном, шкалой, нумерацией и отображением некоторых значений на осях при помощи маркеров.

Изменение диапазона осей. Когда график создается впервые, MathCAD выбирает представленный диапазон для обеих координатных осей автоматически. Чтобы изменить этот диапазон:

1. Постройте график зависимости sin(z) быстрым способом. Диапазон по оси x изменяется от -10 до10.

2. Перейдите к редактированию графика, щелкнув в его пределах мышью (рис. 14).

Рис. 14. Изменение диапазонов осей

3. График будет выделен, а вблизи каждой из осей появится два поля с числами, обозначающими границы диапазона.

4. Измените диапазон оси z на (0,20) и второй оси – на (-2,2). Получится новый график (рис. 15)

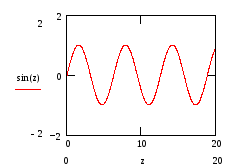
Рис. 15. Результат изменения диапазонов осей

5. Сохраните изменения в текущем документе.

Форматирование шкалы. Изменение внешнего вида шкалы, нанесенной на координатную ось, производится с помощью диалогового окна Formatting Currently Selected X-Y Plot (Форматирование выбранного графика), в котором следует выбрать вкладку X-Y Axes (Оси X-Y) (рис.16).

Вызвать окно можно двойным щелчком мыши в области графика или выполнением команды Format, Graph, X-Y Plot (Формат, График, X-Y зависимость), или выбором в контекстном меню команды Format (Формат).

С помощью флажков и переключателей легко поменять внешний вид каждой из осей:

• Log Scale (Логарифмическая шкала) – график по этой оси будет нарисован в логарифмическом масштабе. Это полезно если данные разнятся на несколько порядков;

• Grid Lines (Вспомогательные линии) – показывают линии сетки;

• Numbered (Нумерация) – если убрать флажок, то числа, размечающие шкалу, пропадут.

• Autoscale (Автомасштаб) – выбор диапазонов оси производится автоматически;

• Show Markers (Показать метки) – выделение значений на осях;

• AutoGrid (Авто сетка) – разбиение шкалы производится автоматически;

• Equal Scales (Равные масштабы) – при снятом флажке оси x и y принудительно рисуются в одинаковом масштабе;

Рис. 16. Окно для форматирования шкалы

• Axes Style (Стиль осей графика) – можно выбрать один из трех видов системы координат:

  • Boxed (Ограниченная область) – область графика ограничена прямоугольником;

  • Crossed (Пересечение) – координатные оси в виде двух пересекающихся прямых;

  • None (Без границ) – координатные оси не показаны на графике.

Задание 2. На примере графиков, приведенных на рис. 17, исследуйте возможности флажков и переключателей диалогового окна Formatting Currently Selected X-Y Plot (Форматирование выбранного графика).

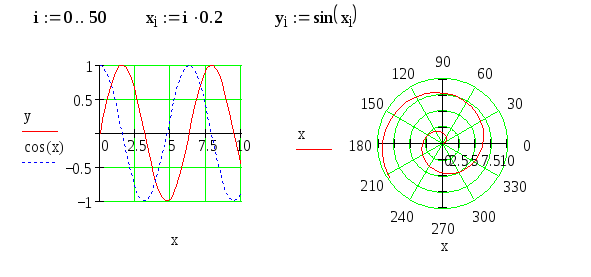
Рис. 17. Линии сетки на декартовом и полярном графиках, вид осей -Crossed

Сохраните изменения в текущем документе.