3. Системы оду первого порядка

MathCAD требует, чтобы система дифференциальных уравнений была представлена в стандартной форме:

y₀'(t)=f₀(y₀(t),y₁(t),…, y_N-1(t),t),

y₁'(t)= f₀(y₀(t),y₁(t),…, y_N-1(t),t), (1)

…

y_N-1'(t)= f_N-1(y₀(t),y₁(t),…, y_N-1(t),t)

Задание системы (1) эквивалентно следующему векторному представлению:

Y'(t)=F(Y(t),t), (2)

где Y и Y' – соответствующие неизвестные векторные функции переменной t размера N×1, а F – векторная функция того же размера и (N+1) количества переменных (N компонент вектора и, возможно, t). Именно векторное представление (2) используется в среде MathCAD для ввода системы ОДУ.

Для того чтобы определить задачу Коши для системы ОДУ, следует определить еще N начальных условий, задающих значение каждой из функций y_i(t0) в начальной точке интегрирования системы t0. В векторной форме они могут быть записаны в виде:

Y(t0)=B, (3)

где B – вектор начальных условий размера N×1, составленный из y_i(t0).

Здесь задача сформулирована для систем ОДУ первого порядка. Если в систему входят уравнения высших порядков, то ее можно свести к системе большего числа уравнений первого порядка.

3.1. Встроенные функции для решения системы оду

В MathCAD имеются три встроенные функции, которые позволяют решать поставленную в форме (2-3) задачу Коши различными численными методами.

1. rkfixed(y0,t0,t1,M,D) –метод Рунге-Кутты с фиксированным шагом.

2. Rkadapt(y0,t0,t1,M,D) - метод Рунге-Кутты с переменным шагом.

3. Bulstoer(y0,t0,t1,M,D) – метод Булирша-Штера.

В этих функциях: y0 – вектор начальных значений в точке t0 размера N×1; t0 – начальная точка расчета; t1 – конечная точка расчета; M – число шагов, на которых численный метод находит решение; D – векторная функция размера N×1 двух аргументов – скалярного t и векторного y. При этом y – искомая векторная функция аргумента t того же размера N×1.

Каждая из приведенных функций выдает решение в виде матрицы размера (M+1)×(N+1). В ее левом столбце находятся значения аргумента t, а в остальных N столбцах - значения искомых функций y₀(t), y₁(t),…, y_N-1(t), рассчитанные для этих значений аргумента. Всего в этой матрице M+1 строка.

В подавляющем большинстве случаев достаточно использовать первую функцию rkfixed.

Задание 4. Реализуйте следующий пример, содержащий решение системы ОДУ модели осциллятора с затуханием. Проанализируйте результаты решения.

Функция D(t,y), определяющая систему ОДУ, имеет ряд особенностей:

1. Функция D должна быть обязательно функцией двух аргументов.

2. Второй ее аргумент должен быть вектором того же размера, что и сама функция D.

Точно такой же размер должен быть и у вектора начальных значений y0.

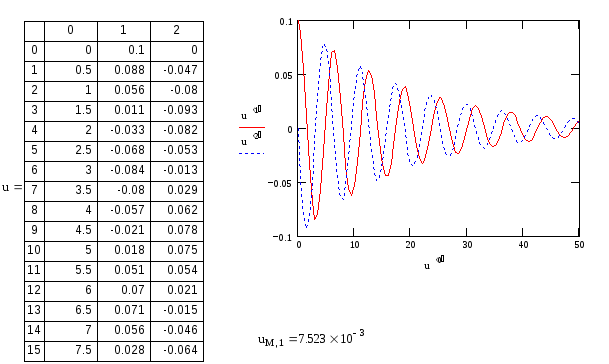
Решение системы осуществлено на промежутке (0, 50). Матрица решений имеет размер (M+1)×(N+1), т.е. 101×3. Просмотреть все компоненты матрицы u можно с помощью вертикальной полосы прокрутки, которая появляется при щелчке мышкой по таблице решений. Так расчетное значение первой искомой переменной y₀ на 12 шаге u_12,1=0.07. Для вывода элементов решения в последней точке интервала используется выражение типа u_M,1=7.523·10^-3.

Чтобы построить график решения, надо отложить соответствующие компоненты решения по координатным осям: значение аргумента u^<0> - вдоль оси X, а u^<1> и u^<2> - вдоль оси Y (Чтобы разместить на рисунке два графика параметры u^<1> и u^<2> для оси Y надо вводить через запятую).

Решение ОДУ часто удобнее изображать в фазовом пространстве, по каждой оси которого откладываются значения каждой из найденных функций. При этом аргумент входит в них лишь параметрически. В случае двух ОДУ такой график – фазовый портрет системы – является кривой на фазовой плоскости и поэтому особенно нагляден.

Задание 5. По условиям задание 4 постройте фазовый портрет. Постройте второй фазовый портрет при M= 200. Проанализируйте результаты решения.

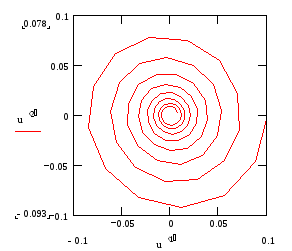
В общим случае, если система состоит из N ОДУ, то фазовое пространство является N-мерным. При N>3 наглядность теряется, и для визуализации фазового портрета приходится строить его различные проекции.

Все численные методы решения ОДУ основаны на аппроксимации дифференциальных уравнений разностными аналогами. В зависимости от конкретной формы аппроксимации, получаются алгоритмы различной точности и быстродействия. В MathCAD использован наиболее популярный алгоритм Рунге-Кутты четвертого порядка, описанный в большинстве книг по методам вычислений. Он обеспечивает малую погрешность для широкого класса систем ОДУ за исключением жестких систем. Поэтому в большинстве случаев применяют функцию rkfixed. Если по различным причинам время расчетов становится критичным или точность неудовлетворительна, стоит попробовать применить другие встроенные функции.

Функция Rkadapt может быть полезна в случае, когда известно, что решение на рассматриваемом интервале меняется слабо, либо существуют участки медленных и быстрых изменений. Метод Рунге-Кутты с переменным шагом разбивает интервал не на равномерные шаги, а более оптимальным способом. Там, где решение меняется слабо, шаги выбираются более редкими, а в областях его сильных изменений – частыми. В этом случае для достижения одинаковой точности требуется меньшее число шагов. Метод Булирша-Штера (Bulstoer) часто оказывается более эффективным для поиска гладких решений.