4. Собственные векторы и собственные значения матриц

Другой важной задачей линейной алгебры является задача поиска собственных векторов x и собственных значений λ квадратной матрицы A, т. е. решение матричного уравнения A·x=λ·x. Такое уравнение имеет решение в виде собственных значений λ1,λ2,… и соответствующих им собственных векторов x1,x2,… Для решения таких задач в MathCAD встроено несколько функций:

1. eigenvals(A) – вычисление вектора, элементами которого являются собственные значения матрицы A.

2. eigenvecs(A) – вычисляет матрицу, содержащую нормированные собственные векторы, соответствующие собственным значениям матрицы A. n-й столбец вычисляемой матрицы соответствует собственному вектору n-го собственного значения, вычисляемого eigenvals.

3. eigenvec(A,λ) – вычисляет собственный вектор для матрицы A и заданного собственного значения λ.

Задание 27. Реализуйте следующие примеры и проанализируйте полученные результаты:

Произведите проверку правильности выражения A·x=λ·x, проведя ее дважды – сначала на числовых значениях x и λ, а потом путем перемножения соответствующих матричных компонентов.

MathCAD позволяет рассмотреть и более общую задачу, называемою задачей на обобщенные собственные значения: A·x=λ·B·x. В ее формулировке помимо матрицы A присутствует еще одна квадратная матрица B. Для решения этой задачи имеются две встроенные функции:

• genvals(A,B) – вычисляет вектор v собственных значений, каждый из которых удовлетворяет задаче на обобщенные собственные значения;

• genvecs(A,B) – вычисляет матрицу, содержащую нормированные собственные векторы, соответствующие собственным значениям в векторе v, который вычисляется с помощью genvals. В этой матрице i-й столбец является собственным вектором x, удовлетворяющим задаче на обобщенные собственные значения.

Задание 28. Реализуйте следующие примеры и проанализируйте полученные результаты:

1. Поиск обобщенных собственных векторов и собственных значений можно осуществить так:

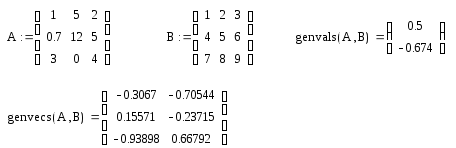
2. Проверку правильности нахождения собственных векторов и собственных значений проведите так:

Современная вычислительная линейная алгебра – бурно развивающаяся наука. Главная проблема, рассматриваемая ею, - это проблема решения систем линейных уравнений. В настоящее время разработано множество методов, упрощающих эту задачу. Большинство методов основано на представлении матрицы в виде произведения других матриц специального вида, или матричных разложений. Как правило, после определенного разложения матрицы задача линейной алгебры существенно упрощается. В MathCAD имеется несколько встроенных функций, реализующих алгоритмы наиболее популярных матричных разложений: разложение Холецкого, QR- разложение, LU- разложение, сингулярное разложение [1].

Лабораторное занятие 6. Обыкновенные дифференциальные уравнения

Дифференциальные уравнения – это уравнения, в которых неизвестными являются не переменные (т.е. числа), а функции одной или нескольких переменных. Эти уравнения (или системы) включают соотношения между искомыми функциями и их производными. Если в уравнение входят производные только по одной переменной, то они называются обыкновенными дифференциальными уравнениями (ОДУ). В противном случае говорят об уравнениях в частных производных. Таким образом, решить (проинтегрировать) дифференциальное уравнение – значит определить неизвестную функцию на определенном интервале изменения ее переменных.

Одно дифференциальное уравнение или система ОДУ имеет единственное решение, если помимо уравнения определенным образом заданы начальные или граничные условия.

Имеется два типа задач, которые можно решать с помощью MathCAD:

• задачи Коши – для которых определены начальные условия на искомые функции, т.е. заданы значения этих функций в начальной точке интегрирования уравнения;

• краевые задачи – для которых заданы определенные соотношения сразу для обеих границ интервала.

Как правило, решение задач Коши для ОДУ и их систем – задача, хорошо разработанная и с вычислительной точки зрения не слишком сложная. Большое значение здесь имеет представление результатов и анализ зависимостей решения от различных параметров системы. Между тем, имеется целый класс ОДУ, называемых жесткими, который не поддается решению стандартными методами, типа Рунге-Кутты. Для них в MathCAD имеются специальные возможности.