1. Оду первого порядка

Дифференциальное уравнение первого порядка может по определению содержать помимо самой искомой функции y(t) только ее первую производную y’(t). В подавляющем большинстве случаев дифференциальное уравнение можно записать в стандартной форме (форме Коши):

y'(t)=f(y(t),t),

и только с такой формой умеет работать вычислительный процессор MathCAD. Правильная с математической точки зрения постановка соответствующей задачи Коши для ОДУ первого порядка должна, помимо самого уравнения, содержать одно начальное условие – значение функции y(t₀) в некоторой точке t₀. Требуется явно определить функцию y(t) на интервале от t₀ до t₁. По характеру постановки задачи Коши называют еще задачами с начальными условиями, в отличие от краевых задач.

Для численного интегрирования одного ОДУ можно использовать либо вычислительный блок Given/Odesolve, либо встроенные функции. Первый путь позволяет наглядно представить задачу и результаты, а второй дает пользователю больше средств для воздействия на параметры численного метода. Исследуем оба варианта решения.

1.1. Вычислительный блок Given/Odesolve

Вычислительный блок для решения одного ОДУ, реализующий численный метод Рунге-Кутты, состоит из трех частей:

• Given – ключевое слово;

• ОДУ и начальные условия, записанные с помощью логических операторов, причем начальное условие должно быть в форме y(t0)=b;

• odesolve(t,t1) – встроенная функция для решения ОДУ относительно переменной t на интервале (t0,t1). Допустимо задание функции odesolve(t,t1,step) с тремя параметрами, где step –внутренний параметр численного метода, определяющий количество шагов, в которых метод Рунге-Кутты будет рассчитывать дифференциальное уравнение. Чем больше step, тем с лучшей точностью будет получен результат, но тем больше времени будет затрачено на его поиск.

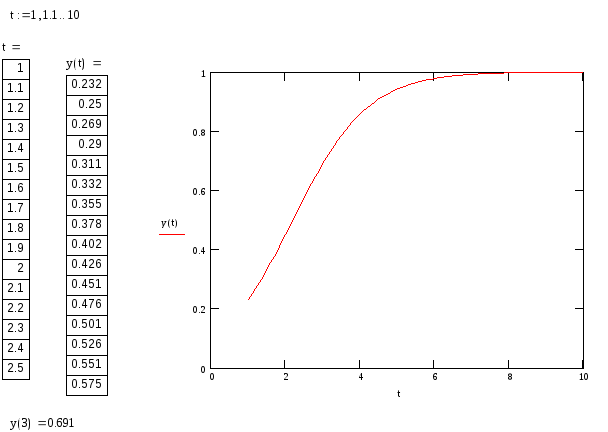
Задание 1. Реализуйте следующий пример и проанализируйте полученные результаты:

Результатом применения блока Given/Odesolve является функция y(t), определенная на промежутке (t0,t1). Можно построить график этой функции, используя графические средства MathCAD, или получить значения в какой-либо точке.

1.2. Встроенные функции rkfixed, Rkadapt, Bulstoer

Для решения ОДУ можно использовать встроенные функции. Этот способ несколько проигрывает первому как в простоте, так и наглядности и используется в ранних версиях MathCAD.

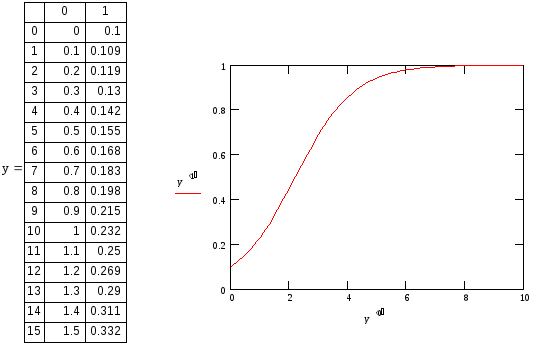
Задание 2. Реализуйте следующий пример и проанализируйте полученные результаты:

Результат решения здесь представлен не в виде функции, а в виде матрицы размерности M×2. Она состоит из двух столбцов: в одном находятся значение аргумента t (от t0 до t1 включительно), а в другом соответствующие значения искомой функции y(t). График решения соответствует получению решения в матричном виде, поэтому по осям отложены соответствующие столбцы, выделенные их матрицы y оператором Столбец матрицы (M^<>)

2. Оду высшего порядка

Обыкновенное дифференциальное уравнение с неизвестной функцией y(t), в которое входят производные этой функции вплоть до y^(N)(t), называются ОДУ N-го порядка. Если имеется такое уравнение, то для корректной постановки задачи Коши требуется задать N начальных условий на саму функцию y(t) и ее производные от первого до (N-1)-го порядка включительно.

В MathCAD можно решать ОДУ высших порядков как с помощью вычислительного блока Given/Odesolve, так и путем сведения их к системам уравнений первого порядка.

Внутри вычислительного блока:

• ОДУ должно быть линейно относительно старшей производной, т.е. фактически должно быть поставлено в стандартной форме;

• начальные условия должны иметь форму y(t)=b или y^(N)(t)=b, а не более сложную (как, например: y(t)+y'(t)=b).

В остальном, решение ОДУ высших порядков ничем не отличается от решения уравнений первого порядка.

Задание 3. Откройте новый документ и решите задачу Коши для ОДУ второго порядка. Проанализируйте полученные результаты.

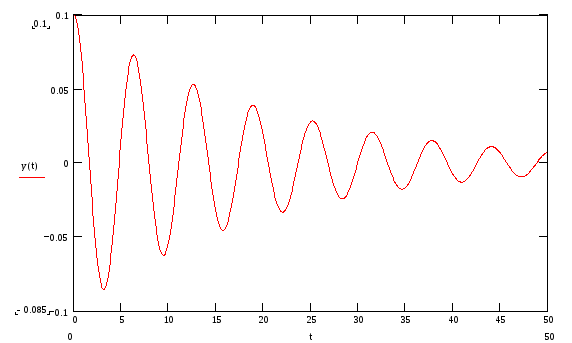
В этом задании решено уравнение затухающего гармонического осциллятора, который описывает, например, колебания маятника. Для модели маятника y(t) описывает изменения угла отклонения от вертикали, y'(t) – угловая скорость маятника (для ввода символа производной используется левая верхняя клавиша символьной клавиатуры), y'' (t) – ускорение, а начальные условия, соответственно, начальное отклонение маятника y(0)=0.1 и начальная скорость y'(0)=0.

Второй способ решения ОДУ высшего порядка связан со сведением его к эквивалентной системе ОДУ первого порядка. Если обозначить y₀(t)≡y(t), а

y₁(t) ≡y'(t)=y₀'(t), тот исходное уравнение запишется через функции y₀(t) и y₁(t) в виде системы двух ОДУ:

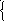y₀'=y₁,

y₁'+0.1·y₁+1·y₀=0.

Методика решения такой системы приведена в следующем разделе.