
- •Часть 4
- •Введение
- •Лекция 1. Система математических расчетов MathCad и особенности ее применения
- •1. Общая характеристика системы MathCad
- •2. Информационная среда, предоставляемая в распоряжение пользователя
- •3. Входной язык, встроенные функции и модули системы MathCad
- •3.1. Входной язык системы MathCad
- •3.2. Основные модули системы MathCad
- •Лабораторное занятие 1: Вычисления и типы данных
- •1. Вычисление значений арифметических и алгебраических выражений
- •2. Переменные, функции и операторы
- •2.1. Переменные
- •2.2. Функции
- •2.3. Операторы
- •3. Данные в MathCad
- •3.1 Типы данных
- •3.2. Размерные переменные
- •4. Массивы
- •4.1. Создание массивов
- •4.2. Ранжированные переменные
- •Лабораторное занятие 2. Создание графиков
- •1. Двумерная графика
- •1.4. Полярный график
- •1.5. Построение нескольких рядов данных
- •1.6. Форматирование осей
- •1.7. Форматирование рядов данных
- •1.8. Трассировка и увеличение графиков
- •2. Трехмерная графика
- •2.1 Создание трехмерной графики
- •2.2. Форматирование трехмерных графиков
- •Лабораторное занятие 3. Символьные вычисления
- •1. Символьная алгебра
- •1.1.Разложение выражений (Expand)
- •1.2. Упрощение выражений (Simplify)
- •1.3. Разложение на множители (Factor)
- •1.4. Приведение подобных слагаемых
- •1.5. Определение коэффициентов полинома (Polynomial Coefficients)
- •1.6. Разложение на элементарные дроби
- •1.7. Подстановка переменной (Substitute)
- •1.8. Решение алгебраических уравнений (solve)
- •1.9. Суммы и произведения
- •2. Символьное решение задач математического анализа
- •2.1. Дифференцирование (Differentiate) и интегрирование (Integrate)
- •2.2. Разложение в ряд (Expand to Series)
- •2.3. Интегральные преобразования
- •3. Дополнительные возможности символьного процессора
- •3.1. Применение функций пользователя
- •3.2. Получение численного значения выражений
- •3.3. Последовательности символьных команд
- •Лабораторное занятие 4. Численные методы
- •1. Интегрирование и дифференцирование
- •1.1. Интегрирование
- •1.2. Дифференцирование
- •2. Алгебраические уравнения и оптимизация
- •2.1. Одно уравнение с одним неизвестным
- •2.2. Корни полинома
- •2.3. Системы уравнений
- •2.4. Символьное решение уравнений
- •3. Поиск экстремума функции
- •3.1. Экстремум функции одной переменной
- •3.2. Условный экстремум
- •3.3. Экстремум функции многих переменных
- •3.4. Линейное программирование
- •Лабораторное занятие 5. Матричные вычисления
- •Простейшие операции с матрицами
- •Транспонирование
- •Сложение
- •1.3. Умножение
- •1.4. Определитель квадратной матрицы
- •1.5. Модуль вектора
- •1.6. Скалярное произведение векторов
- •1.7. Векторное произведение
- •1.8. Сумма элементов вектора и след матрицы
- •1.9. Обратная матрица
- •1.10. Возведение матрицы в степень
- •1.11. Векторизация массивов
- •2.1.2. Создание матриц специального вида
- •2.2. Слияние и разбиение матриц
- •2.2.1. Выделение части матрицы
- •2.2.2. Слияние матриц
- •2.3. Сортировка матриц
- •2.4. Вывод размера матриц
- •2.5. Норма квадратной матрицы
- •2.6. Число обусловленности квадратной матрицы
- •2.7. Ранг матрицы
- •3. Система линейных уравнений
- •4. Собственные векторы и собственные значения матриц
- •Лабораторное занятие 6. Обыкновенные дифференциальные уравнения
- •1. Оду первого порядка
- •1.1. Вычислительный блок Given/Odesolve
- •1.2. Встроенные функции rkfixed, Rkadapt, Bulstoer
- •2. Оду высшего порядка
- •3. Системы оду первого порядка
- •3.1. Встроенные функции для решения системы оду
- •3.2. Решение системы оду в одной точке
- •Приложения Приложение 1. Встроенные функции и операторы
- •Встроенные функции
- •Приложение 2. Сообщения об ошибках
- •Оглавление
4.2. Ранжированные переменные
Ранжированные переменные (дискретные переменные) в MathCAD являются разновидностью векторов и предназначены, главным образом, для создания циклов или итерационных вычислений. Простейший пример ранжированной переменной – это массив с числами, лежащими в некотором диапазоне с некоторым шагом. Например:
0, 2, 4, 6, 8, 10.
Задание 17. Создайте несколько ранжированных переменных, выполнив следующие команды:
-
Выберите место расположения переменной.
-
Введите имя переменной и оператор присваивания

Рис. 5. Создание ранжированной переменной
-
Нажмите кнопку Range Variable (Задать диапазон дискретной величины) на палитре Matrix (Матрицы), либо введите символ точки с запятой с помощью клавиатуры.
-
В появившиеся местозаполнители (рис. 5) ведите левую и правую границу диапазона изменения ранжированной переменной, например: 0 и 5 и нажмите клавишу Enter.
-
Выведите значение дискретной переменной.
-
Чтобы создать ранжированную переменную с шагом отличные от 1, выполните следующие шаги:
-
введите имя переменной, оператор присваивания и создайте ранжированную переменную y.
-
в первый местозаполнитель введите левую границу диапазона (первый элемент массива), затем вставьте запятую и запишите значение второго элемента.
-
во второй местозаполнитель вставьте последнее значение диапазона, нажмите клавишу Enter и выведите значения созданной ранжированной переменной

-
Сохраните изменения в текущем документе.
Реализуйте следующие примеры использования ранжированных переменных:


Последнее задание:
-
Самостоятельно формулируйте выводы из проведенных исследований.
-
Сохраните результаты всей работы в отдельной папке.
Лабораторное занятие 2. Создание графиков
В MathCAD встроено несколько типов графиков, которые можно разбить на две большие группы.
-
Двумерные графики:
-
XY (декартовый) график (XY Plot);
-
полярный график (Polar Plot).
-
Трехмерные графики:
-
график трехмерной поверхности (Surface Plot);
-
график линий уровня (Contour Plot);
-
трехмерная гистограмма (3D Bar Plot);
-
трехмерное множество точек (3D Scatter Ploy);
-
векторное поле (Vector Field Plot).
Все графики создаются совершенно одинаково, с помощью палитры Graph (Графики) или команды меню Insert, Graph (Вставка, График).
1. Двумерная графика
1.1. XY-график двух векторов
Самый простой способ получения декартового графика – это сформировать два вектора данных, которые будут отложены вдоль осей X и Y.
Задание 1. Построить график двух векторов x и y, выполнив следующие операции:
-
Откройте новый документ.
-
Введите ранжированную переменную i:
![]()
-
Определите элементы двух векторов:
![]()
-
Выведите значения векторов x и y:

Рис. 6. Построение графика двух векторов
-
На панели инструментов Math (Математика) нажмите кнопку с изображением графиков (Инструменты графиков). Откроется палитра Graph (Графики), на которой нужно выбрать команду X-Y Plot (Декартов график).
-
В местозаполнители возле осей введите имена векторов x и y. (В местозаполнители можно ввести элементы векторов xi и yi ). Щелкните по пустому месту документа и получите график двух векторов. На графике отложены точки, соответствующие парам элементов векторов, соединенные отрезками прямых линий. Используя угловой маркер, увеличьте размер графика.
-
Сохраните документ в своей папке под именем Графика 2.
1.2. XY- график вектора и ранжированной переменной
В качестве переменных, откладываемых по любой из осей, можно использовать саму ранжированную переменную. При этом по другой оси должно быть отложено либо выражение, явно содержащее саму ранжированную переменную, либо элемент вектора с индексом по этой ранжированной переменной, но никак не сам вектор. Например:
![]()

Рис. 7. Графики векторов и ранжированной переменной
Сохраните изменения в текущем документе.
1.3. XY-график функции
Нарисовать график любой скалярной функции f(x) можно двумя способами. Первый способ заключается в дискретизации значений функции, присвоении этих значений вектору и прорисовке графика вектора. Второй, более простой способ, называемый быстрым построением графика, заключается во введении функции в одно из местозаполнителей, а имени аргумента – в местозаполнитель у другой оси. В результате MathCAD сам создаст график функции в пределах значений аргумента, по умолчанию принятых равными от -10 до10. Разумеется, впоследствии можно поменять диапазон значений аргумента, и график автоматически подстроится под него. На рис. 8 представлен график функции sin(x), построенный быстрым способом. Второй график представлен с учетом изменений значений аргумента. При таком способе построения графика корректировать шаг изменения аргумента нельзя, и не все функции можно представить таким образом (в основном, только элементарные).
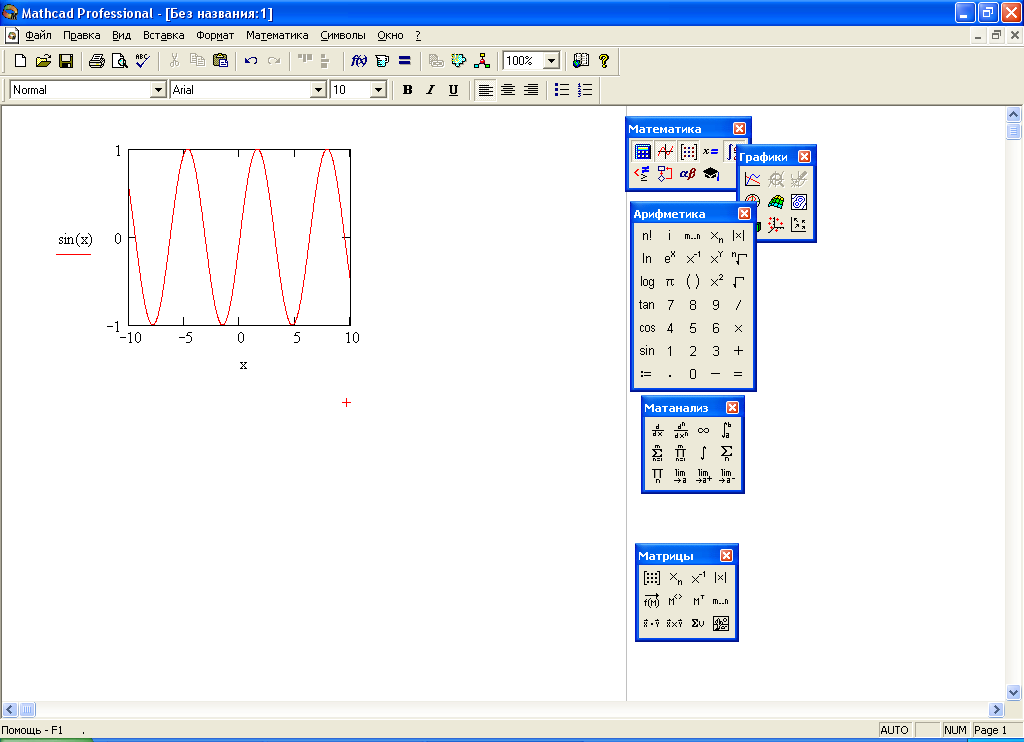

Рис. 8. Быстрое построение графика функции
Необходимо заметить, что если переменной аргумента функции было присвоено некоторое значение до построения в документе графика, то вместо быстрого построения графика будет нарисована зависимость функции с учетом этого значения. Примеры двух таких графиков приведены на рис. 9.

Рис. 9. Графики функций от векторного аргумента
Сохраните изменения в текущем документе.
