Многомерное дискретное преобразование Фурье

Двумерный дискретный ряд Фурье можно представить в виде

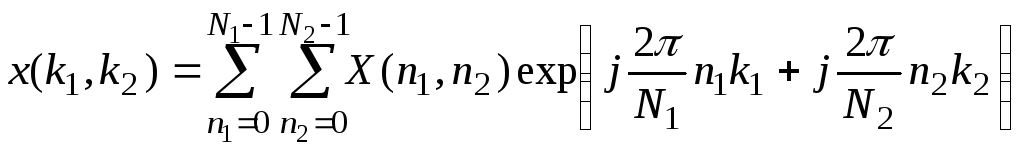
где - коэффициенты ряда Фурье,

- комплексная синусоида, прямоугольно-периодичная с горизонтальным N₁ и вертикальным N₂ периодом.

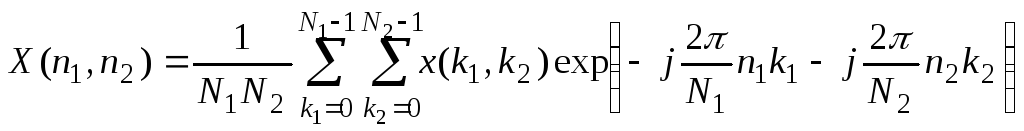
Свойства дискретного преобразования Фурье

В целом свойства ДПФ аналогичны свойствам непрерывного преобразования Фурье, однако дискретный характер анализируемого сигнала привносит некоторую специфику.

Линейность

Из формулы (3) очевидно, что ДПФ является линейным, то есть если последовательностям {x(k)} и {y(k)} с одним и тем же периодом N соответствуют наборы гармоник Х(п) и Y(n), то последовательности {ax(k) + by(k)} будет соответствовать спектр аХ(п)+ bY(n).

Задержка(смещение) функции

Если задержать исходную последовательность на один такт (y(k) = x(k-1)), то, согласно (3), спектр необходимо умножить на ехр(-j2πп/N):

Поскольку мы считаем последовательность {x(k)} периодической, рассматриваемый здесь сдвиг является циклическим: y(0) = х(-1) = x(N - 1).

Изменение масштаба аргумента функции

Симметрия

Как уже отмечалось, спектр дискретного периодического сигнала является периодическим. Кроме того, сохраняется и свойство симметрии, которым обладает спектр непрерывного вещественного сигнала (). Поэтому

. (5)

Гармоника с нулевым номером (постоянная составляющая), как видно из (3), представляет собой сумму отсчетов последовательности на одном периоде:

(6)

Если N четно, то амплитуда гармоники с номером N/2 является суммой отсчетов с чередующимися знаками:

Согласно (5), спектр является «сопряженно-симметричным» относительно N/2, то есть содержит ровно такое же количество информации, что и сам сигнал. В самом деле, исходная последовательность представляется набором из N вещественных чисел. Спектр же представляется набором из N/2 (вторая половина взаимно-однозначно связана с первой) комплексных чисел, каждое из которых с информационной точки зрения эквивалентно двум вещественным. Если же исходная последовательность {х(k)} не является вещественной, симметрия спектра отсутствует и N комплексным отсчетам во временной области соответствует N комплексных отсчетов в спектральной области.

Дпф произведения последовательностей

Возьмем две последовательности отсчетов {х₁(k)} и (x₂(k)} одинаковой длины N и вычислим результат их поэлементного умножения:

.

Если применить к этой формуле прямое ДПФ, получится следующее выражение:

. (7)

ЗАМЕЧАНИЕ ----------------------------------------------------------------------------------------

При выполнении вычислений по формуле (7) могут понадобиться значения с номерами i выходящими за рамки диапазона 0…N-1. В этом случае следует воспользоваться свойством периодичности спектра: .

Это выражение представляет собой круговую свертку спектров и . Итак, как и для непрерывного преобразования Фурье, спектр произведения является сверткой спектров.

При п=0 из (7) получается дискретный аналог теоремы Рэлея (см. «Энергетические расчеты в спектральной области»):

. (5.8)

При выводе формулы (8) были использованы соотношения (5) и (6).

Если, кроме того, последовательности {x₁(k)} и {x₂(k)} совпадают, то есть x₁{k)=x₂(k)=x(k) для всех k=0...N-1, из (5.8) получается дискретный аналог равенства Парсеваля (см.«Энергетические расчеты в спектральной области» и формулу :

.