3.4. Специальные случаи решения задач линейного программиро­вания

В п. 3.1 были выделены разные варианты решения задачи линейного программирования. Сформулируем их еще раз:

1) решение задачи может быть единственной точкой;

2) решение задачи может иметь альтернативный оптимум и быть представлено линейной комбинацией нескольких точек;

3) оптимального решения может не существовать, поскольку оно неограниченно (сверху или снизу);

4) решения может не существовать, поскольку ОДЗ – пустое множество точек.

Рассмотрим, каким образом проявляют себя данные ситуации при решении задач симплекс-методом.

Пример 3.5. Пусть в примере 3.2 цена стола составляет не 30, а 35 у.е. Тогда решая эту задачу получим, что последняя симплекс-таблица (табл. 3.4) будет иметь вид:

Базис	СБ		х1	х2	х3	S1	S2	S3	S4	с. о.
			60	35	20	0	0	0	0
S1	0	24	0	-2	0	1	2	-8	0	–
x3	20	8	0	-2	1	0	2	-4	0	–
x1	60	2	1	5/4	0	0	-1/2	3/2	0	1,6
S4	0	5	0	1	0	0	0	0	1	5
		280	0	0	0	0	10	10	0	max

Данное решение оптимально и совпадает с решением в табл. 3.4: x₁ = 2, x₂ = 0, x₃ = 8, Z = 280. Однако нужно заметить, что при небазисной переменной x₂ в индексной строке стоит ноль (снижающая оценка равна нулю), то есть эту переменную можно ввести в базис и целевая функция не изменится. Это говорит о наличии другого оптимального решения.

Таким образом, признаком альтернативного оптимума является коэффициент 0 в строке при небазисной переменной.

Введем переменную x₂ в базис:

Базис	СБ		х1	х2	х3	S1	S2	S3	S4
			60	35	20	0	0	0	0
S1	0	27,2	1,6	0	0	1	1,2	–5,6	0
x3	20	11,2	1,6	0	1	0	1,2	-1,6	0
x2	35	1,6	0,8	1	0	0	-0,4	1,2	0
S4	0	3,4	–0,8	0	0	0	0,4	–1,2	1
		280	0	0	0	0	10	10	0

Получим еще одно оптимальное решение с тем же значением целевой функции: x₁ = 0, x₂ = 1,6, x₃ = 11,2, Z = 280.

Общее решение получается линейной комбинацией:

(2; 0; 8) + (1–)(0; 1,6; 11,2), где 0    1.

Так, например, если взять  = 0,375, получим решение: x₁ = 0,75; x₂ = 1; x₃ = 10, которое тоже дает z = 280.

Пример 3.6. Рассмотрим задачу:

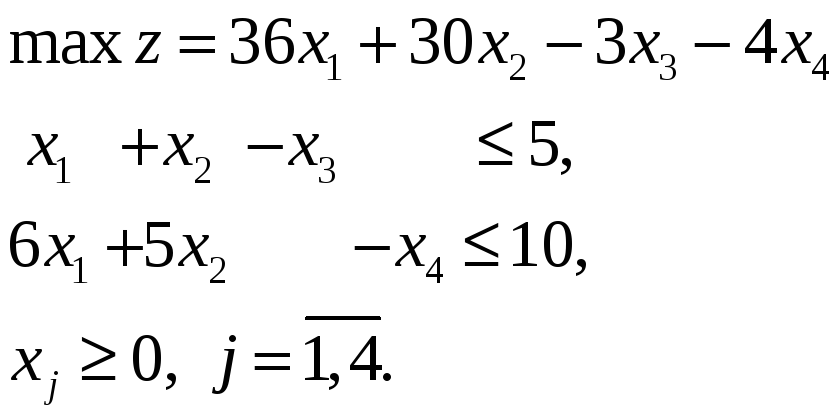
Введя в модель дополняющие переменные S₁ и S₂, решим ее симплекс-методом:

Базис	сj		х1	х2	х3	х4	S1	S2	с. о.
			36	30	-3	-4	0	0
S1	0	5	1	1	-1	0	1	0	5
S2	0	10	6	5	0	-1	0	1	1,67
		0	-36	-30	3	4			max

Базис	сj		х1	х2	х3	х4	S1	S2	с. о.
			36	30	-3	-4	0	0
S1	0	20/6	0	1/6	1	1/6	1	-1/6	20
x1	36	10/6	1	5/6	0	-1/6	0	1/6	–
		60	0	0	3	-2	0	6	max

Базис	сj		х1	х2	х3	х4	S1	S2	с. о.
			36	30	-3	-4	0	0
x4	-4	20	0	1	-6	1	6	-1	–
x1	36	5	1	1	-1	0	1	0	–
		60	0	2	-9	0	12	4

В последней таблице в строке ЦФ получили, что решение еще не оптимально, так как при переменной x₃ отрицательный элемент (–9) и она должна войти в базис. Однако нельзя выбрать переменную, которая могла покинуть базис. Это значит, что как ни увеличивай значение x₃, целевая функция будет всегда увеличиваться (на 9 единиц на каждую единицу x₃) при этом переменные x₁ и x_4­ никогда не станут отрицательными (не станут равны нулю и не выйдут из базиса) – они тоже будут расти. Такая ситуации говорит о том, что решение задачи неограниченно.

Таким образом, если свободная переменная имеет отрицательный коэффициент в строке целевой функции (в задаче на максимум) и все неположительные коэффициенты в разрешающем столбце, то задача является неограниченной, то есть всегда можно найти решение лучше предыдущего.

Пример 3.7. Рассмотрим задачу:

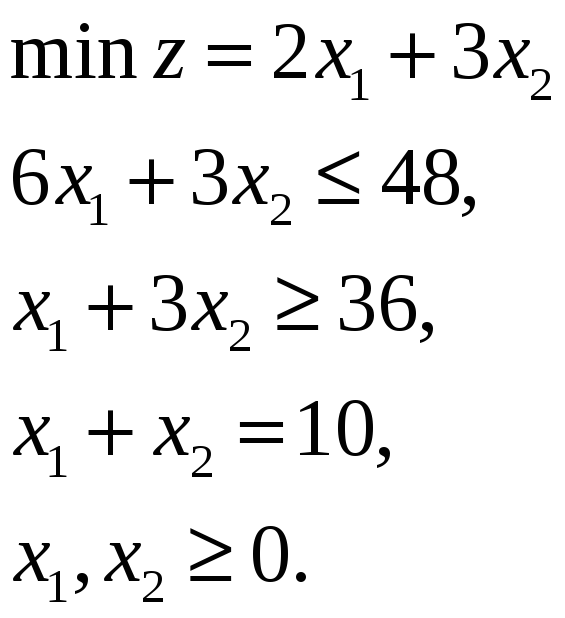
Будем решать задачу методом искусственного базиса:

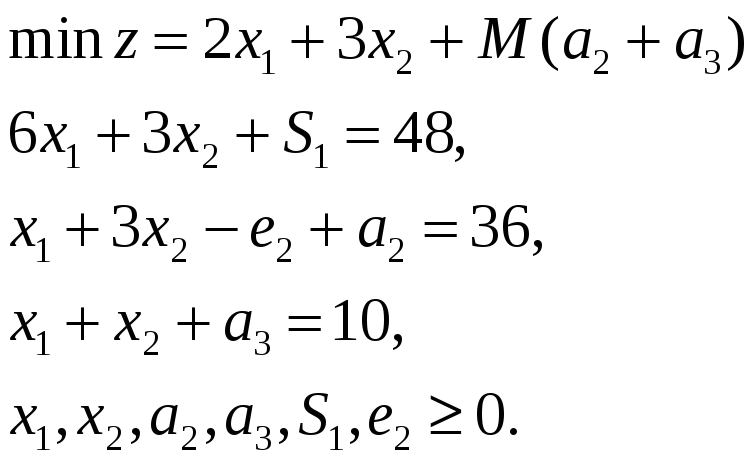
Имеем:

,

.

Базис	cj		х1	х2	S1	e2	a2	a3	с.о.
			2	3	0	0	M	M
S1	0	48	6	3	1	0	0	0	16
a2	M	36	1	3	0	–1	1	0	12
a3	M	10	1	1	0	0	0	1	10
	–	0	–2	–3	0	0	0	0	min
	M	46	2	4	0	–1	0	0	min

Базис	cj		х1	х2	S1	e2	a2	a3
			2	3	0	0	M	M
S1	0	18	3	0	1	0	0	–3
a2	M	6	–2	0	0	–1	1	–3
x2	3	10	1	1	0	0	0	1
	–	30	1	0	0	0	0	3
	M	6	–2	0	0	–1	0	–4

Поскольку все элементы второй строки целевой функции неположительные, оптимальное значение М-задачи найдено, однако переменная a₂ не вышла из базиса, z₂ = 6M  0 и z = 30 + 6M. Это обозначает, что исходная задача не имеет решения, так как ограничения несовместимы, то есть ОДЗ – пустое множество.