Тема 3 задачи линейного программирования и методы их решения

3.1. Графический метод решения задач линейного программи­рования

Рассмотрим следующую задачу производственного планирования.

Пример 3.1. Для изготовления двух видов продукции I и II используют четыре вида ресурсов R1, R2, R3 и R4. Запасы ресурсов, число еди­ниц ресурсов, затрачиваемых на изготовление единицы продук­ции, приведены в таблице:

Вид ресурса	Запас ресурса	Число единиц ресурсов, затрачиваемых на изготовление одной единицы продукции
		I вид	II вид
R1	18	1	3
R2	16	2	1
R3	5	-	1
R4	21	3	-

Прибыль, получаемая от реализации одной единицы продукции I и II вида, соот­ветственно, 2 и 3 грн.

Необходимо составить такой план производства продукции с учетом имеющихся ресурсов, при котором прибыль от ее реализации будет максимальной.

Пусть x₁ – число производимых единиц продукции I вида, x₂ – II вида. Тогда математическая запись модели имеет вид:

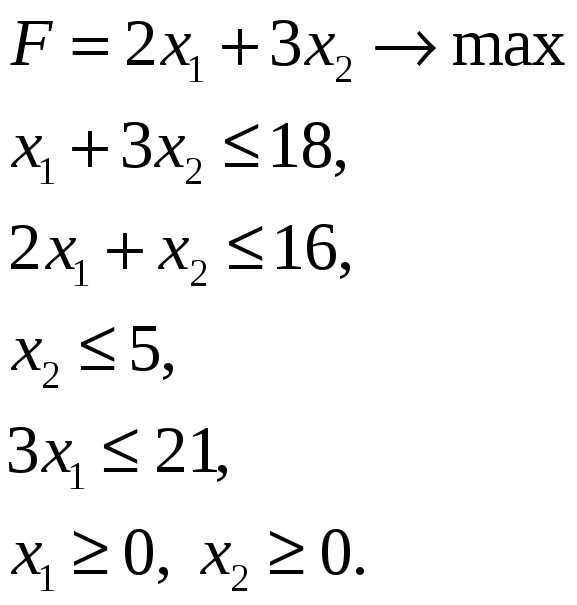
Решим данную задачу графическим методом.

Графическим методом задача решается в 2 этапа.

1 этап: построение области допустимых значений переменных.

Сначала построим систему координат: на горизонтальной оси будут указываться значения переменной а на вертикальной – Кроме того, условие неотрицательности переменных показывает, что область допустимых значений (ОДЗ) будет лежать в первом квадранте (то есть выше оси и правее оси ).

Если в каждом ограничении заменить знак неравенства (≥ или ≤) на равенство, то полученные уравнения будут представлять собой прямые на плоскости в системе координат x₁ и x₂. Каждая из таких прямых делит плоскость на два полупространства, знак же неравенства (≥ или ≤) в исходных ограничениях позволяет определить, какое из двух полупространств удовлетворяет ограничению, а какое нет. Точки плоскости, расположенные по одну сторону прямой, удовлетворяют неравенству, а точки, лежащие по другую сторону, – нет. Чтобы определить нужную полуплоскость, можно в соответствующее ограничение подставить любую точку, не лежащую на данной прямой. Если в итоге получилось верное неравенство, та полуплоскость, в которой находилась подставленная точка, удовлетворяет ограничению. Если же получилось неравенство противоречивое, то ограничению удовлетворяет противоположная полуплоскость.

Рассмотрим прямую из первого ограничения Для построения этой прямой достаточно подобрать любые две точки, которые бы удовлетворяли уравнению. Например, если x₁ = 0, то должно быть x₂ = 18/3 = 6. Имеем одну точку (0; 6). Если x₁ = 6, то должно быть x₂ = (18–6)/3 = 4. Имеем одну вторую точку (6; 4). Через эти две точки можно однозначно повести прямую (часть этой прямой, отрезок BC, показан на рис. 3.1). Чтобы определить, какая полуплоскость нам подходит (выше прямой или ниже), подставим в ограничение какую-нибудь точку, не лежащую на прямой BC. Из рис. 3.1 видно, что такой точкой может быть, например, точка (0; 0). Получим: – верное неравенство. Значит, подходит нижняя полуплоскость – та, в которой находится точка (0; 0).

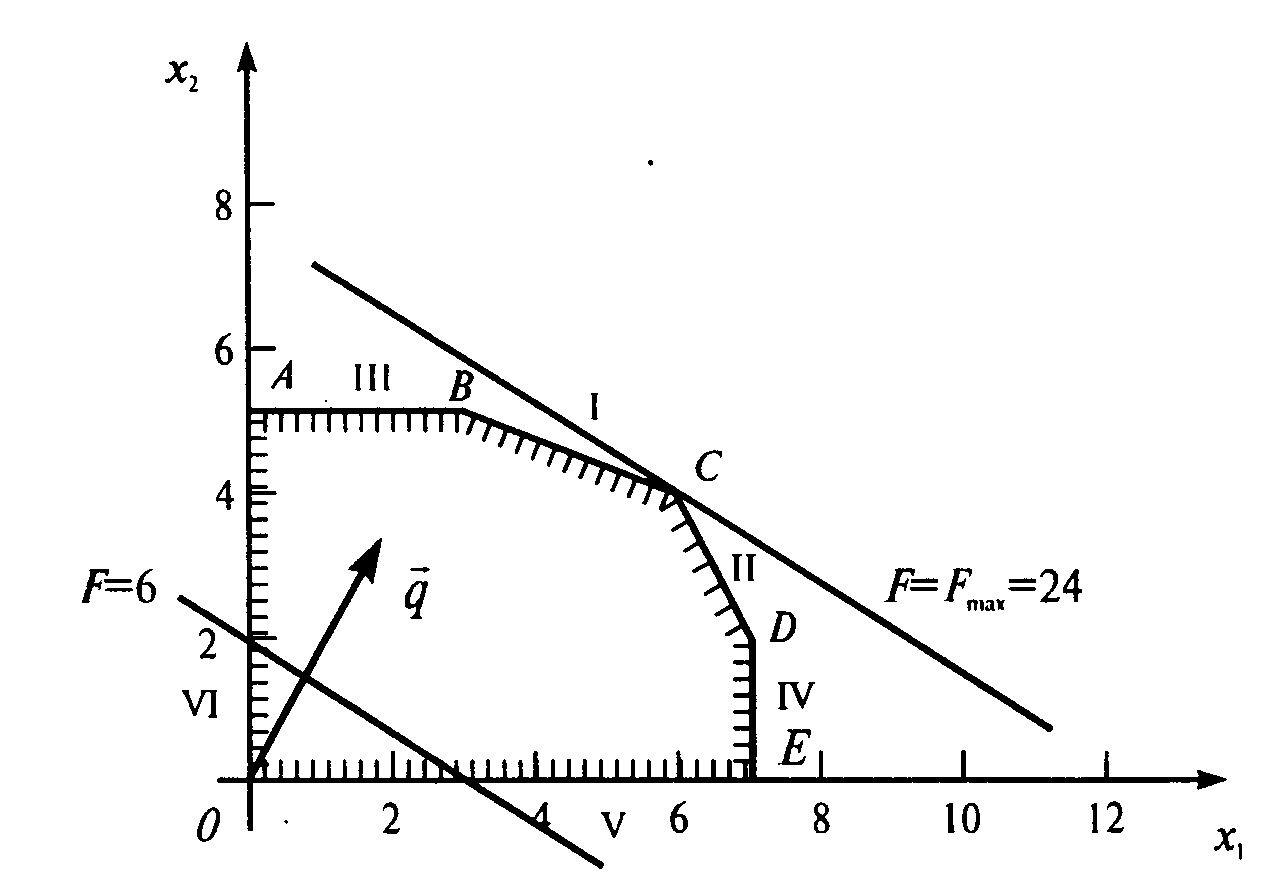
Рис. 3.1. Решение задачи линейной оптимизации графическим способом

Заметим, что если бы мы подставили, например, точку (6; 6), которая тоже не лежит на прямой BC, получили бы противоречивое неравенство . Тогда сделали бы вывод, что верхняя полуплоскость (где находится точка (6; 6)) не подходит, а значит подходит противоположная, нижняя, полуплоскость.

Рассмотрим прямую второго ограничения . Подберем произвольные две точки для ее построения. При x₂ = 0, x₁ = 16/2 = 8. При x₂ = 6, x₁ = (16–6)/2 = 5. Через точки (0; 8) и (6; 5) проводим прямую (часть этой прямой, отрезок CD, показан на рис. 3.1). Тестовой точкой для проверки того, точки какого полупространства удовлетворяют неравенству, а какого – нет, опять же удобно взять точку (0,0): Это означает, что область допустимых значений нашей задачи располагается левее прямой СD.

Прямая x₂ = 5 располагается горизонтально (отрезок AB на рис. 3.1), – ей удовлетворяют точки с произвольной координатой x₁, координата же x₂ всегда равна 5. В ограничении x₂ ≤ 5 подходит нижняя полуплоскость.

Прямая 3x₁ = 21, или что эквивалентно, x₁ = 7, располагается вертикально (отрезок DE на рис. 3.1), – ей удовлетворяют точки с произвольной координатой x₂, координата же x₁ всегда равна 7. В ограничении 3x₂ ≤ 21 подходит левая полуплоскость.

В итоге, объединив все допустимые полуплоскости вместе, получим многоугольник ОABCDE, представленный на рис. 3.1, который и есть областью допустимых значений задачи. Только точки из этого многоугольника удовлетворяют всем ограничениям задачи, точки вне его хотя бы одному из ограничений не удовлетворяют и являются недопустимыми.

2 этап: поиск оптимального решения.

Из всех точек ОДЗ (которых бесконечное множество) теперь необходимо найти ту, которая дает наибольшее значении функции .

Для того чтобы найти оптимальное решение, необходимо определить направление возрастания целевой функции (напомним, что функцию F следует максимизировать). Для этого строится вектор-градиент, который показывает направление наиболее быстрого роста функции в определенной точке. Рассчитывается градиент так:

grad F = .

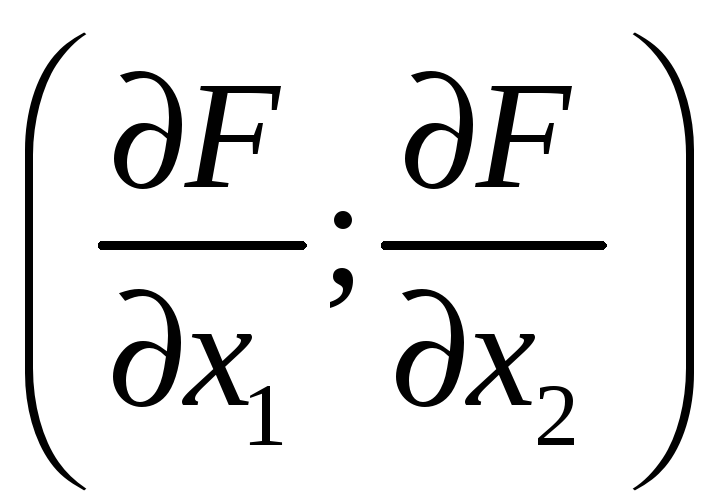Если целевая функция нелинейная то в каждой точке значение градиента может быть разное, то есть целевая функция в разных точках может иметь разное направление и скорость роста. Для линейной целевой функции вектор-градиент является константой и не зависит от того к какой точке он построен. Производная линейной целевой функции по x₁ и x₂ совпадает с коэффициентами целевой функции c₁ и с₂. Поэтому для построения градиента линейной задачи достаточно построить вектор, исходящий из начала координат (0; 0) и направленный в точку .

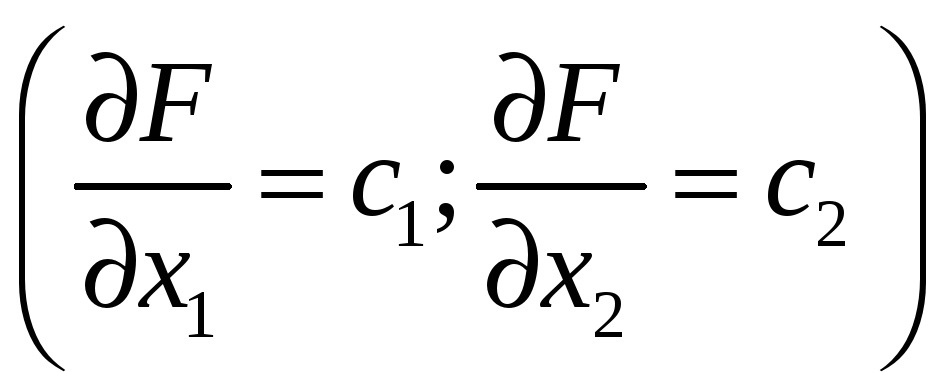Таким образом, возвращаясь к примеру 3.1, построим градиент , направленный в точку (2; 3) – см. рис. 3.1.

Градиент показывает, что в точках, расположенных дальше по направлению вектора, целевая функция будет принимать большие значения.

Если перпендикулярно градиенту построить прямую (в произвольном месте), во всех точках данной прямой значение целевой функции будет одним и тем же. Например, прямая , проходящая через точки (0; 2), (3; 0), перпендикулярна градиенту (рис. 3.1). Во всех ее точках целевая функция принимает значение, равное 6. Подобного рода прямые называются изоцелью или линиями уровня.

Если в направлении градиента откладывать линии уровня как можно дальше, но так, чтобы хотя бы одна из точек линии уровня находилась в пределах ОДЗ, можно найти точку, которая дает наибольшее значение целевой функции. Исходя из рис. 3.1 видно, что самой крайней изоцелью в пределах ОДЗ будет изоцель, проходящая через точку С, находящейся на пересечении прямых BC и СD. Эта точка и будет оптимальным решением, дающим максимум целевой функции.

Поскольку координаты этой точки нам не известны, чтобы их найти, нужно решить систему из двух уравнений, соответствующих прямым, пересечение которых дает искомую точку. Прямая BC описывалась уравнением прямая CD – уравнением . Решим систему:

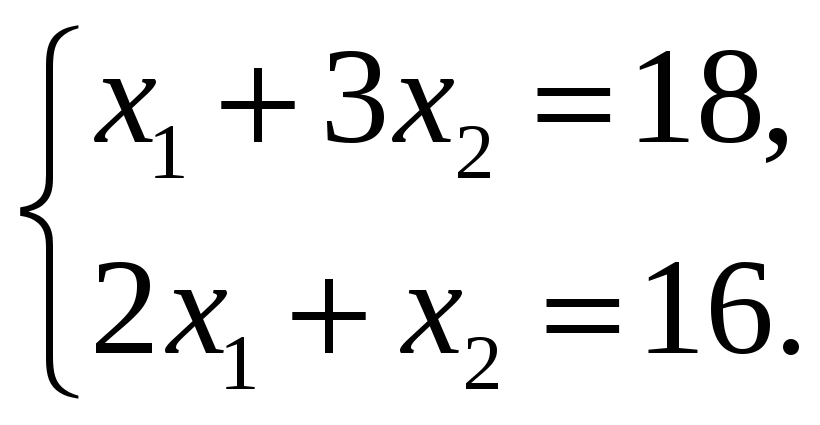
Вычтем из второго уравнения удвоенное первое, чтобы избавится от переменной x₁, получим: 2x₁ – 2x₁ + x₂ – 6x₂ = 16 – 36  –5x₂ = –20  x₂ = 4. Подставим данное значение x₂, например, в первое уравнение, получим x₁ + 12 = 18  x₁ = 6.

Таким образом, точка С(6; 4) и есть оптимальное решение задачи. При выпуске 6 единиц продукции I вида и 4 единиц продукции II прибыль достигает максимального значения: F = 2·6 + 3·4 = 24.

Сформулируем несколько замечаний.

1. Начать построение ОДЗ удобно с ограничений на знак переменных (если они есть), тогда ОДЗ сразу уменьшается до I квадранта.

2. Определять изменения в ОДЗ нужно последовательно: построив одну из прямых ограничений и выбрав соответствующую полуплоскость, сразу определить, как это повлияет на уменьшение ОДЗ и какая часть плоскости отсечется. Это упрощает идентификацию ОДЗ, поскольку объединить все допустимые полуплоскости одновременно при большом количестве ограничений бывает затруднительно.

3. Вполне возможна ситуация, когда построенное ограничение не влияет на уменьшение ОДЗ. Например, если в примере 3.1 добавить ограничение x₁ ≤ 10, то оно не повлияет на существующее ОДЗ, поскольку является избыточным (существующее ограничение x₁ ≤ 5 более жесткое).

4. Если решается задача на минимум, то изоцели нужно строить в направлении, противоположном градиенту. В примере 3.1 при решении этой задачи на минимум, крайней изоцелью оказалась бы прямая, проходящая через точку (0; 0) и эта точка была бы оптимальным решением.

5. Оптимальное решение задачи всегда находится на границе ОДЗ и никогда не может быть внутренней точкой ОДЗ, поскольку в том случае всегда можно провести более удаленную изоцель.

6. Графическим методом легко может быть решена только задача с двумя переменными, поскольку в этом случае задача решается на плоскости. Если задача с тремя переменными, то для ее решения нужно строить трехмерное пространство и ограничения будут представлять собой плоскости, а ОДЗ – многогранник. В трехмерном пространстве, очевидно, можно решить только достаточно простые задачи. Задачи с большим числом переменных, чем 3, графическим способом решить нельзя, поскольку трудно себе представить и визуализировать многомерное пространство.

На основании решения задачи примера 3.1 формулируем ряд важных понятий.

Ограничение называется связующим, если в результате подстановки в него оптимальных значений переменных оно выполняется как строгое равенство.

В примере 3.1 связующими были два ограничения и . Именно на пересечении соответствующих связующим ограничениям прямых и находится оптимальное решение задачи.

Если левая часть ограничения не равна правой, такое ограничение называется несвязующим. Несвязующими в задаче 3.1 были ограничения x₁ ≤ 5 и

Любое изменение в связующих ограничениях однозначно приводит к изменению оптимального решения задачи. Если же удалить несвязующие ограничения, оптимальное решение не изменится.

Связующие ограничения показывают, почему нельзя улучшить целевую функцию. В примере 3.1 этого нельзя сделать, поскольку ресурсы R1 и R2 (соответствующие первому и второму ограничениям) полностью исчерпаны. Эти ресурсы называются критическими или дефицитными. При этом ресурса R3 осталось неиспользованным 1 единица (5 – 4), а ресурса R4 – 3 единицы (21 – 3∙6). Ресурсы R3 и R4 являются некритическими.

В зависимости от того, как выглядит ОДЗ задачи линейного программирования, выделяют специальные случаи ее решения. ОДЗ задачи линейного программирования может быть:

1. Выпуклым ограниченным множеством.

Множество точек называется выпуклым, если вместе с двумя любыми своими точками оно содержит отрезок, соединяющий эти точки.

Множество точек назовём ограниченным, если найдётся сфера конечного радиуса с центром в начале координат, содержащая все точки этого множества.

На рис. 3.2 примеры а, б, г, д, е отражают выпуклые множества, в – невыпуклое множество. Примеры а, б, в отражают ограниченные множества, г, д, е – неограниченные.

а) б) в)

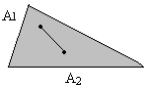
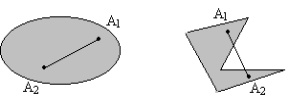
г) д) е)

Рис. 3.2. Примеры множеств

Если ОДЗ – выпуклое ограниченное множество, в этом случае возможные решения задачи находятся в угловых точках этого множества.

В некоторых частных случаях, когда крайняя изоцель параллельна грани (совпадает с ней), оптимальным решением будут все точки этой грани. Например, пусть в задаче 3.1 целевая функция имеет вид . В этом случае градиент будет направлен в точку (1; 3), а крайняя изоцель совпадет с гранью BC. Чтобы выписать все решения нужно найти две угловые (крайние) точки этой грани (B и C). Точка С нам уже известна (6; 4), точка B образована пересечением прямых и x₂ = 5. Тогда, решив эту систему, получим x₂ = 18 – 3∙5 = 3, то есть точка B имеет координаты (3; 5). Составим линейную комбинацию из точек B и С:

, где .

Это и будет общим решением. Например, при  = 0,5 получим новую оптимальную точку: (0,5∙3+0,5∙4; 0,5∙5+0,5∙6) = (3,5; 5,5). Изменяя  от 0 до 1, решение будет «пробегать» отрезок BC от точки C (при  = 0) до точки B (при  = 1).

Такое оптимальное решение, когда оно не единственное, называется альтернативным оптимумом.

2. ОДЗ может быть отдельной точкой. В этой ситуации лишь одна точка (часто в подобных случаях этой точкой оказывается точка (0;0)) удовлетворяет всем ограничениям. Очевидно, что в этом случае решение единственно, оно находится в этой точке и является оптимальным (независимо от целевой функции).

3. ОДЗ может быть неограниченным выпуклым множеством.

В этом случае решение может находиться или в угловой точке (в частности совпадать с гранью и являться альтернативным оптимумом), или быть неограниченно. В последнем случае нельзя провести крайнюю изоцель, всегда найдется такая изоцель в пределах ОДЗ, которая дает еще лучшее значение целевой функции. Такая ситуация возникает тогда, когда задача имеет некорректную постановку. В этой ситуации, несмотря на то, что существует множество допустимых решений, оптимального решения не существует, поскольку оно неограниченно. Если значения переменных можно до бесконечности увеличивать, говорят, что задача неограниченна сверху, если уменьшать – неограниченна снизу.

4. ОДЗ может быть пустым множеством точек. Такая ситуация возникает, если система ограничений противоречива. Например, x₁ ≥ 5 и x₁ ≤ 4. Очевидно, что в этом случае не существует не только оптимального решения, но и ни одного допустимого решения. Опять же такая ситуация может возникнуть при некорректной постановке задачи.

Таким образом, если задача линейного программирования имеет оптимальное решение, то это решение находится в угловой точке ОДЗ или выражается через комбинацию угловых точек ОДЗ (в случае альтернативного оптимума). Угловые точки ОДЗ представляют множество допустимых решений задачи (ОДР).

Таким образом, в отличие от ОДЗ, ОДР представляет собой конечное (счетное) число угловых точек, которые потенциально могут быть оптимальным решением. Никакие другие точки ОДЗ оптимальным решением быть не могут.