3.3. Метод искусственного базиса

Выделить сразу исходный базис после приведения задачи к стандартному виду удается не всегда. Рассмотрим следующую задачу.

Пример 3.4.

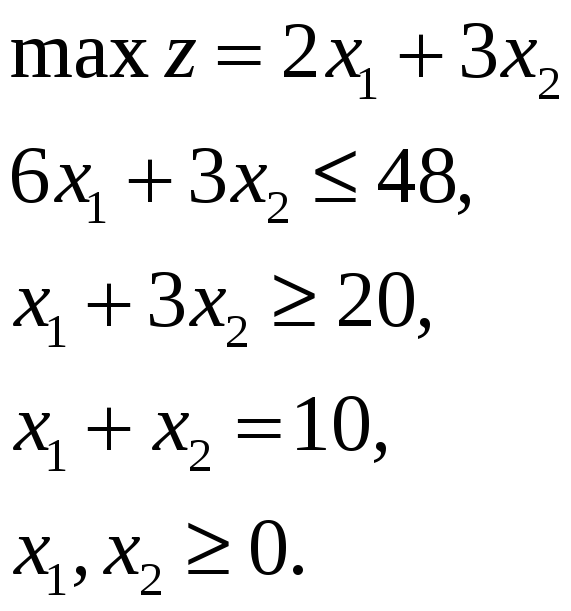
Приведем данную задачу к стандартной форме, прибавив к ограничению типа  добавочную переменную S₁, и вычтя из ограничения типа  избыточную переменную e₂:

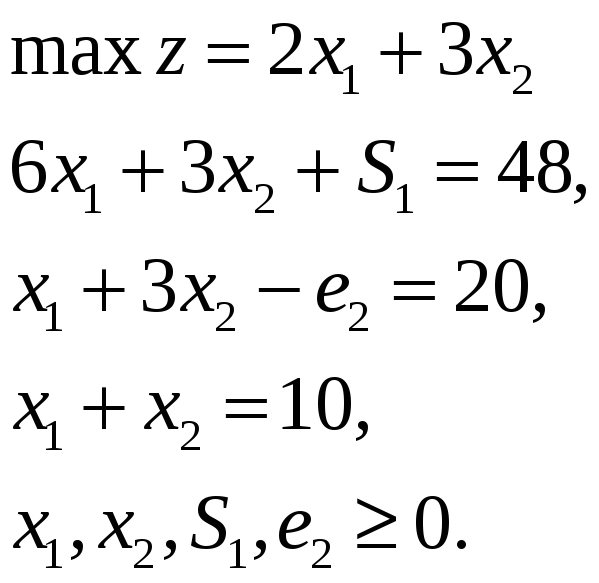
В первом уравнении в качестве базисной можно выбрать переменную S₁. Во втором и третьем уравнении нет переменных, которые могли бы составить исходный базис. (Заметим, e₂ нельзя брать в качестве базисной, поскольку тогда –e₂ = 20, а значение e₂ = –20 недопустимое.)

Для того, чтобы иметь возможность выделить исходный базис во второе и третье ограничения вводятся искусственные переменные a₂, a₃:

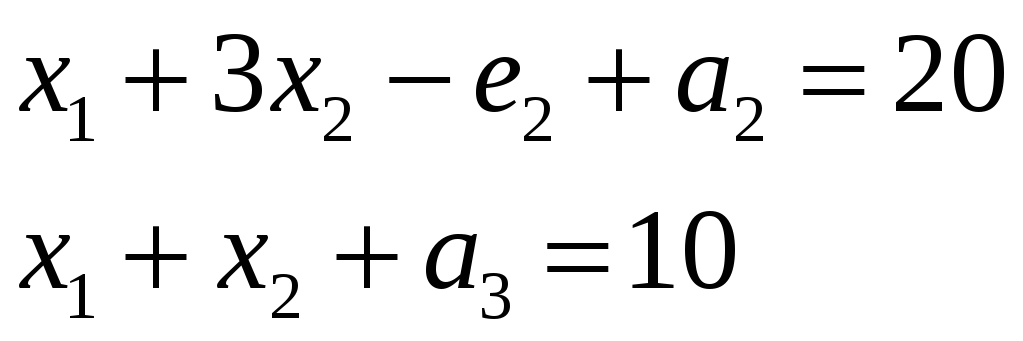(6)

Эти переменные искажают исходные уравнения

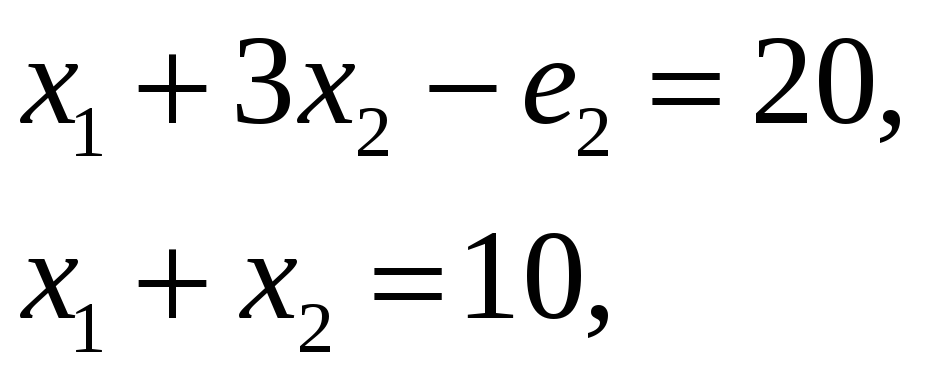(7)

так как, очевидно, (6) будет эквивалентно (7) только в том случае, когда a₂ = a₃ = 0. Если же a₂ или a₃ отличны от нуля, то выполнение системы (6) будет обозначать невыполнение системы (7).

Поэтому вводить искусственные переменные нужно так, чтобы при решении задачи они оказались равными нулю (то есть покинули базис). Для этого модифицируется функция цели – в нее включаются эти переменные с очень большим коэффициентом M так, чтобы любое ненулевое значение этих переменных очень сильно ухудшало целевую функцию. В задаче на min искусственные переменные водятся со знаком + (увеличивая ЦФ), в задаче на max – со знаком «минус» (уменьшая ЦФ).

Тогда задача принимает вид:

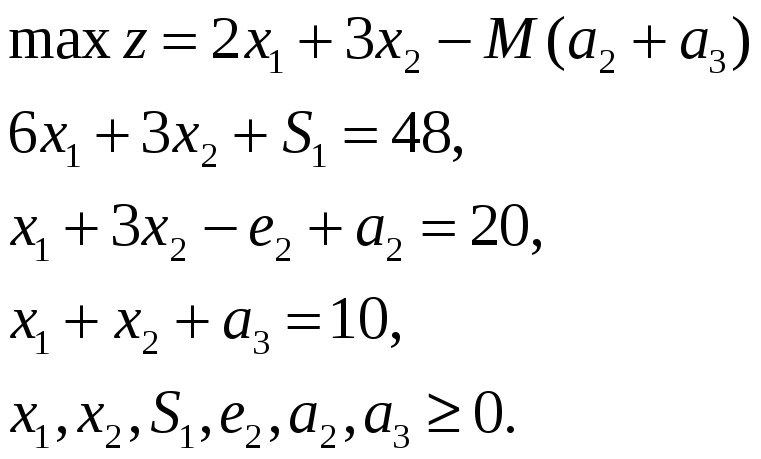
Выделим исходный базис (S₁ = 48, a₂ = 20, a₃ = 10). Выразим из ограничений 2 и 3 переменные a₂, a₃ и подставим в целевую функцию:

,

,

,

.

Заметим, что поскольку a₂ ≥ 0, a₃ ≥ 0, то a₂ + a₃ ≥ 0, а значит выражение в скобках всегда неотрицательное, и уменьшая выражение в скобках, целевая функция z будет увеличиваться. Разобьем целевую функцию на две:

,

.

Заметим, что если бы исходная задача была на минимум, то первая целевая функция должна была бы минимизироваться, вторая – тоже минимизироваться.

Таким образом, вторая ЦФ всегда минимизируется и именно с ее минимизации начинается решение задачи. Часть решения задачи, связанная с минимизацией функции z₂ называется также M-задачей.

В результате решения M-задачи все искусственные переменные должны покинуть базис. Если это происходит – переходят к решению основной задачи, если нет – значит исходная задача не имеет решения.

Построим исходную симплекс-таблицу с учетом двух строк ЦФ:

Базис	cj		х1	х2	S1	e2	a2	a3	с.о.
			2	3	0	0	M	M
S1	0	48	6	3	1	0	0	0	16
a2	M	20	1	3	0	–1	1	0	6,66
a3	M	10	1	1	0	0	0	1	10
	–	0	–2	–3	0	0	0	0	max
	M	30	2	4	0	–1	0	0	min

Сначала минимизируем вторую ЦФ, добиваясь, чтобы она стала равна нулю, и все искусственные переменные вышли из базиса. Так как во второй индексной строке есть положительные элементы и максимальный из них (4) соответствует переменной x₂, то она войдет в базис:

Базис	cj		х1	х2	S1	e2	a2	a3	с.о.
			2	3	0	0	M	M
S1	0	28	5	0	1	1	–1	0	28/5
x2	3	20/3	1/3	1	0	–1/3	1/3	0	20
a3	M	10/3	2/3	0	0	1/3	–1/3	1	5
	–	20	–1	0	0	–1	1	0	max
	M	10/3	2/3	0	0	1/3	–4/3	0	min

Поскольку решается задача на минимум, решение не оптимально, так как во второй индексной строке есть положительные значения 2/3 и 1/3. Переменная x₁ должна войти в базис, так как 2/3 > 1/3.

Базис	cj		х1	х2	S1	e2	a2	a3	с.о.
			2	3	0	0	M	M
S1	0	3	0	0	1	–1,5	1,5	–7,5	–
x2	3	5	0	1	0	–0,5	0,5	–0,5	–
x1	2	5	1	0	0	0,5	–0,5	1,5	10
	–	25	0	0	0	–0,5	0,5	1,5	max
	M	0	0	0	0	0	–1	–1	min

Во второй индексной строке наблюдается оптимум, поскольку в ней нет положительных элементов. Видим, что все искусственные переменные покинули базис и вторая целевая функция равна нулю.

Переходим к решению основной задачи. Рассмотрим первую индексную строку, соответствующую целевой функции основной задачи. Первая индексная строка рассматривается до искусственных переменных (их в базис больше водить никогда не будем). Поскольку исходная задача решается на максимум, в первой индексной строке, есть отрицательный элемент –0,5 при переменной e₂ и ее нужно ввести в базис. Ввести ее в базис можно только вместо переменной x₁.

Заметим, если бы исходная задача была на минимум, то текущее базисное решение (x₁ = 5, x₂ = 5, z = 25) было бы оптимальным, так как в первой индексной строке не положительных элементов.

Базис	cj		х1	х2	S1	e2	a2	a3
			2	3	0	0	M	M
S1	0	18	3	0	1	0	0	–3
x2	3	10	1	1	0	0	0	1
e2	0	10	2	0	0	1	–1	3
	–	30	1	0	0	0	0	3
	M	0	0	0	0	0	–1	–1

Текущее базисное решение оптимальное: x₂ = 10, x₁ = 0, z = 30. Связующим является только последнее ограничение, так как его теневая цена (коэффициент в индексной строке в столбце a₃) отлична от нуля (равна 3). То есть изменение правой части ограничения на 1 единицу приведет к изменению целевой функции на 3 единицы.

Снижающая оценка при переменной x₁ равна 1 (см. индексную строку), это обозначает, что если возникнет необходимость ввести x₁ в базис, то ЦФ ухудшится на 1∙ x₁ единиц.