Тема 6 нелинейные оптимизационные модели экономических систем

6.1. Понятие нелинейных оптимизационных моделей и подходы к их решению

Среди нелинейных задач оптимизации выделяют 2 основных вида:

1. классическая задача математического программирования;

2. задача нелинейного программирования.

Классическая задача имеет вид:

f(x₁, …, x_n)  max

g₁(x₁, …, x_n) = b₁,

g₂(x₁, …, x_n) = b₂, (13)

…

g_m(x₁, …, x_n) = b_m.

То есть в классической задаче все ограничения представляют собой равенства, а функции f, g₁, …, g_m – известные непрерывно дифференцируемые функции, которые могут быть нелинейными.

В матричном виде задачу (13) можно записать так:

f(X)  max

g(X) = b

В такой задаче для существования ее решения должно выполняться n – m ≥ 0, а величина n – m называется числом степеней свободы задачи.

Задача нелинейного программирования отличается тем, что система ограничений представлена в виде неравенств, а на переменные Х наложено ограничение на неотрицательность:

f(x₁, …, x_n)  max

g₁(x₁, …, x_n) ≤ b₁,

g₂(x₁, …, x_n) ≤ b₂, (14)

…

g_m(x₁, …, x_n) ≤ b_m,

x₁ ≥ 0, …, x_n ≥ 0.

Или в матричном виде:

f(X)  max

g(X) ≤ b

Х ≥ 0.

В такой задаче величины n и m не связаны между собой никакими ограничениями. Представленный набор знаков неравенств ≤ совершенно условен, так как любое неравенство можно умножить на –1 и получить знак ≥, а ограничение типа = можно заменить эквивалентной парой ограничений ≤ и ≥. Если в задаче есть переменная, которая не имеет ограничения на знак, скажем x₉, то ее можно заменить двумя переменными x₉ ≥ 0 и x₉ ≥ 0, полагая, что x₉ = x₉ – x₉, так что новая формулировка не будет включать переменной x₉. Таким образом, в виде (14) можно представить любую, в том числе и классическую, задачу математического программирования.

Трудности решения задач классического и нелинейного программирования состоят в том, что:

1) направление и скорость возрастания целевой функции изменяется в зависимости от той точки, в которой находится градиент;

2) ОДЗ задачи может быть невыпуклым множеством;

3) оптимальное решение может находиться не в угловой точке, а в любой из точек кривой, описываемой ограничением;

4) оптимальное решение задачи нелинейного программирования вообще может находиться не в крайней, а во внутренней точке ОДЗ (правда нужно заметить, что в этом случае решение задачи существенно упрощается);

5) аналитические методы часто приводят к нахождению локальных экстремумов, что не гарантирует глобальную оптимальность решения задачи.

Проиллюстрируем особенности решения задач классического и нелинейного программирования графическим методом.

Заметим, что графическим методом, как и в случае с задачами линейного программирования решить можно только задачи с 1-ой или 2-мя переменными.

При n = 2 мы непосредственно определяем только ОДЗ, откладывая переменные по осям x₁ и x₂. Целевая же функция определяется через линии уровня (изоцели) и направление наискорейшего роста (градиент). Напомним, что изоцелью называются такие точки, в которых ЦФ принимает одинаковые значения. Если ЦФ нелинейная – линией уровня будет выступать кривая. Различные константы порождают различные кривые.

Пример 6.1.

.

Ограничение представляет собой уравнение окружности с центром в точке (0; 0) и радиусом 1. Для определения направления возрастания ЦФ найдем градиент:

grad f = = .

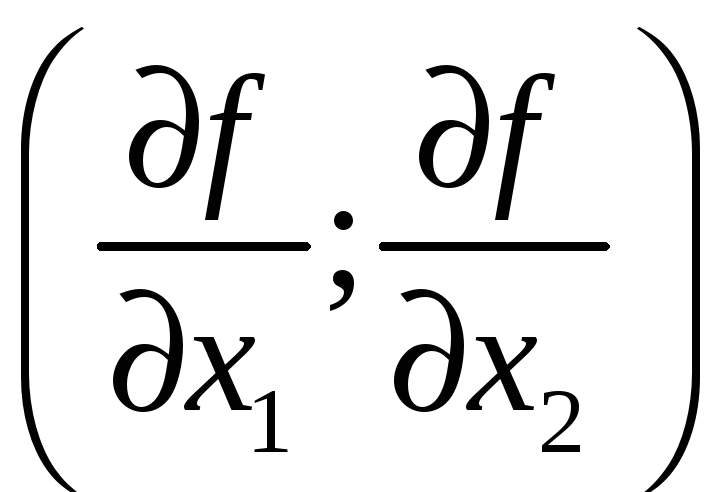Таким образом, в разных точках градиент имеет разные направления:

grad f_(0;0) = (–4; –4); grad f_(1;0) = (–2; –4); grad f_(0;1) = (–4; –2);

grad f_(2;2) = (0; 0); grad f_(2;1) = (0; –2); grad f_(1;2) = (–2; 0);

grad f_(3;1) = (2; –2); grad f_(1;3) = (–2; 2); grad f_(3;3) = (2; 2).

Анализируя направления градиента и значение ЦФ в различных точках, приходим к выводу, что изоцели ЦФ являются концентрическими окружностями с центром в точке (2; 2). Решение задачи показано на рис. 6.1.

Рис. 6.1 Графическое решение классической задачи математического программирования (пример 6.1).

Таким образом, изоцели, расположенные дальше от точки (2;2) дают больший рост ЦФ (градиент больше). При этом максимальное значение ЦФ примет в точке B, а минимальное – в точке А. (Заметим, что глобальный минимум ЦФ находится в точке (2; 2), однако это точка расположена вне ОДЗ, состоящего из точек окружности, и является недопустимым.)

Чтобы найти точки А, B нужно учесть, что в них наклон линии уровня равен наклону кривой допустимых значений переменных. В нашем случае это максимальная точка B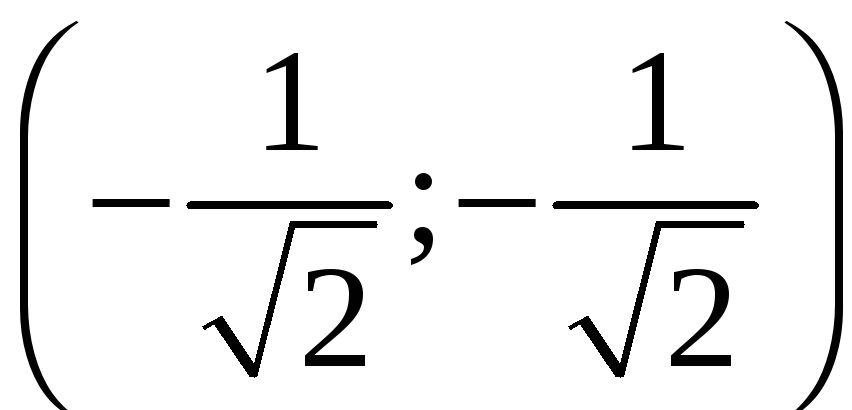 и минимальная точка A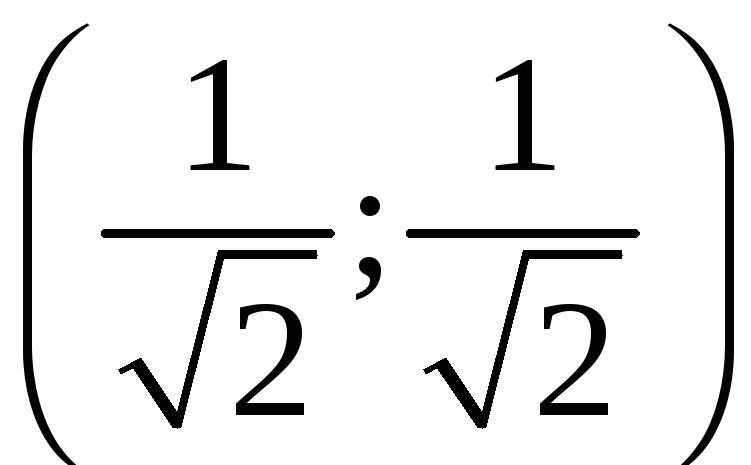, что простейшими геометрическими вычислениями легко можно получить из рис. 6.1, как длину стороны квадрата с диагональю, равной единице.

Тогда f_max = 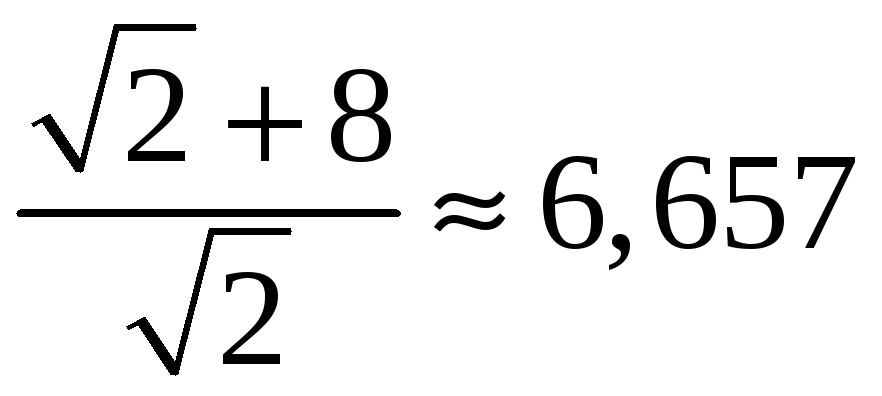, f_min = .

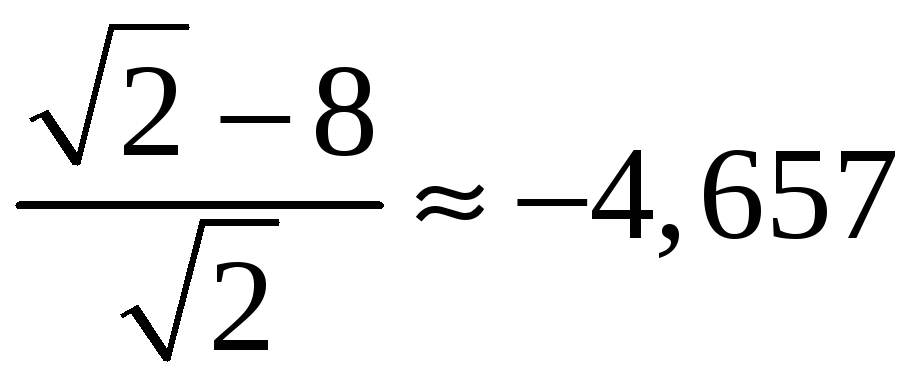Для того чтобы задача нелинейной оптимизации имела единственную оптимальную точку необходимо, чтобы область допустимых значений было ограниченным выпуклым множеством, а непрерывная целевая функция была вогнутой (при задаче на максимум, выпуклой – при задаче на минимум). Однако, часто определить, является ли ОДЗ задачи выпуклым множеством бывает затруднительно.

Что касается задач нелинейного программирования, то здесь могут существовать два типа решений, как показано на рис. 6.2. Решение может находиться как на границе ОДЗ (рис. 6.2 а), так и во внутренней точке (рис. 6.2 б).

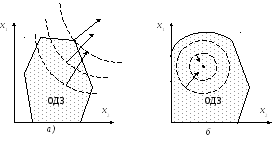
Рис. 6.2. Два типа решения задачи нелинейного программирования: а) граничное решение, б) внутреннее

Для решения классической задачи математического программирования для поиска точек максимума и минимума (экстремальных точек) в условиях как отсутствия, так и наличия ограничений, широко используется аппарат дифференциального исчисления. Наибольшее распространение получили два метода: метод приведенного градиента (или метод Якоби) и метод множителей Лагранжа. Суть последнего метода будет рассмотрена в п. 6.2.

Методы решения задач нелинейного программирования можно условно разделить на 2 класса: прямые и не прямые методы. Примером прямых методов могут служить градиентные методы, где экстремум функции находится последовательно при движении в направлении возрастания или убывания функции в соответствии с вычисленными на каждом шаге значениями градиентов. В непрямых методах исходная задача заменяется (аппроксимируется) другой задачей, оптимальное решение которой можно найти. Сюда относятся методы квадратичного, сепарабельного и стохастического программирования. Рассмотрение этих методов выходит за рамки данного методического издания.

Заметим, что универсальных методов решения задач нелинейного программирования не существует, и это связано, главным образом, с разнообразием нелинейных функций. Наиболее общим подходом, получившим самое широкое распространение и имеющим отношение к рассматриваемым задачам, являются условия Куна-Таккера. Эти условия являются необходимыми (но не достаточными) для существования экстремума, что собственно, все равно еще не гарантирует нахождение оптимального решения.