2.2. Примеры постановки оптимизационных задач

Пример 2.1. Задача планирования производства

Для изготовления продукции двух типов (I, II) требуется четыре вида сырья S₁, S₂, S₃, S₄. На изготовление одной единицы каждого типа продукции требуется разное количество сырья. Запасы сырья ограничены. Прибыль от реализации одной единицы продукции каждого типа известна. Запасы сырья каждого вида, нормозатраты сырья на единицу каждого из типов продукции, а также прибыль от единицы производимой продукции представлены в таблице.

Таблица 2.1 – Исходные данные к примеру 2.1

Виды сырья	Нормозатраты сырья на единицу продукции		Запасы сырья
	I вид	II вид
S1	2	3	19
S2	2	1	13
S3	0	3	15
S4	3	0	18
Прибыль от реализации единицы продукции	7	5

Необходимо определить, сколько продукции каждого вида нужно выпускать, чтобы максимизировать суммарную прибыль предприятия.

Для математического описания любой задачи оптимизации важно определить, что является переменными задачи и как через эти переменные можно выразить целевую функцию и систему ограничений.

В данном случае удобно обозначить: x₁ – количество изготавливаемой продукции I типа, x₂ – количество изготавливаемой продукции II типа.

Тогда прибыль от реализации продукции I типа составит 7x₁, а от реализации второго типа – 5x₁ (свойство пропорциональности). Совокупная прибыль предприятия составит 7x₁ + 5x₁ (свойство аддитивности). То есть целевая функция имеет вид:

z = 7x₁ + 5x₁ → max.

На выпуск единицы продукции первого типа требуется 2 единицы сырья S₁ (см. табл. 2.1), тогда всего сырья S₁ на выпуск x₁ единиц продукции первого типа потребуется 2x₁, на выпуск продукции второго типа – 3x₂. Совокупный расход сырья S₁ на выпуск продукции обоих типов составит 2x₁ + 3x₂, и он не должен превышать запаса этого ресурса в 19 единиц. Таким образом, имеем первое ограничение:

2x₁ + 3x₂ ≤ 19.

Аналогичным образом получаются остальные ограничения задачи:

2x₁ + x₂ ≤ 13,

3x₂ ≤ 15,

3x₁ ≤ 18.

Поскольку по смыслу задачи переменные x₁ и x₂ не могут быть отрицательными, водим ограничения на знак:

x₁ ≥ 0, x₂ ≥ 0.

Заметим, что это не единственно возможная постановка задачи. В качестве переменных можно было бы выбрать следующие: x₁ – количество ресурса S₁, которое расходуется на выпуск продукции I типа, x₂ – количество ресурса S₁, которое расходуется на выпуск продукции II типа, …, x₇ – количество ресурса S₄, которое расходуется на выпуск продукции I типа, x₈ – количество ресурса S₄, которое расходуется на выпуск продукции II типа.

Тогда система ограничений имела бы вид:

x₁ + x₂ ≤ 19,

x₃ + x₄ ≤ 13,

x₅ + x₆ ≤ 15,

x₇ + x₈ ≤ 18,

x_j ≥ 0, .

Однако, при таком определении переменных возникают проблемы с выражением количества выпускаемой продукции и, соответственно, описанием целевой функции. Целевую функцию в этом случае можно представить так:

z = ,

однако, очевидно, что такая функция является нелинейной и решить задачу в такой постановке достаточно сложно. Поэтому первая постановка является предпочтительной.

Пример 2.2. Транспортная задача

На n складах находится соответственно А₁, А₂, ..., А_n некоторого товара. Этот товар необходим k потребителям соответственно в количествах B₁, B₂, ..., B_k единиц. Будем считать, что между предложением и спросом существует баланс, то есть A₁+A₂+ ... +A_n = B₁+B₂+ ... +B_k или .

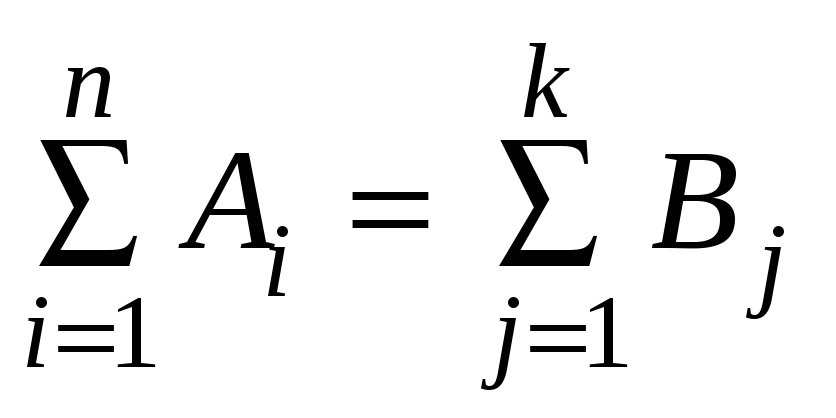Обозначим через с_ij – стоимость перевозки единицы товара от i-го поставщика j-му потребителю. Часто с_ij называют тарифами.

Необходимо составить план перевозок товаров так, что бы общая стоимость перевозок была минимальной.

Вj Аi	B1	B2	. . .	Bk
A1	с11	с12	. . .	с1k
A2	с21	с22	. . .	с2k
. . .	. . .	. . .	. . .	. . .
An	сn1	сn2	. . .	сnk

Пусть x_ij – число единиц товара, перевозимого от i-го поставщика j-му потребителю. Тогда общая стоимость перевозок составит:

z = c₁₁x₁₁ + c₁₂x₁₂ + ... + c_1kx_1k + ... + c_n1x_n1 + c_n2x_n2 + ... + c_nkx_nk .

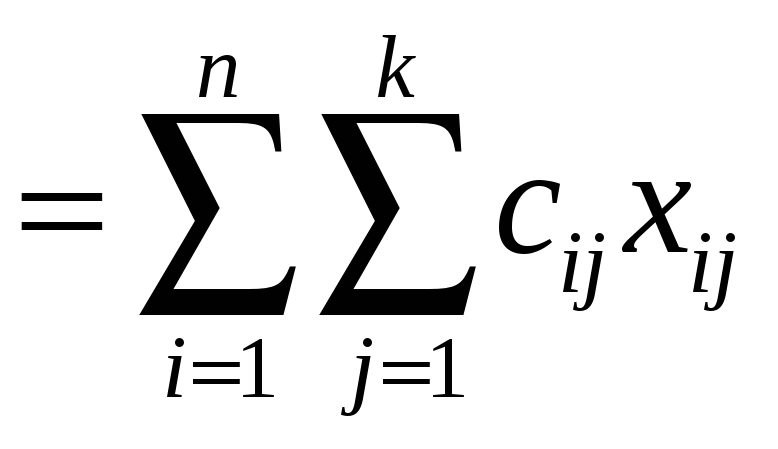При этом должны быть выполнены такие ограничения:

1) все склады должны стать пустыми (вся продукция должна быть вывезена):

x₁₁ + x₁₂ + . . . + x_1k = A₁

. . . . . . . . . . . . . . . . . . .

x_n1 + x_n2 + . . . + x_nk = A_n

2) все потребители должны быть полностью удовлетворены (спрос должен быть удовлетворен в полном объеме):

x₁₁ + x₂₁ + . . . + x_n1 = B₁

. . . . . . . . . . . . . . . . . . .

x_1k + x_2k + . . . + x_nk = B_k

Имеют место также ограничения на знак (нельзя перевезти отрицательное число единиц продукции):

x_ij  0, .

Пример 2.3. Задача на построение расписаний

Больнице скорой помощи в разные дни недели требуется разное число санитаров: в понедельник – 27, во вторник – 23, в среду – 25, в четверг – 29, в пятницу – 24, в субботу – 26, в воскресенье – 21. По требованию профсоюза работник должен трудиться 5 дней подряд, а затем 2 дня отдыхать. Необходимо минимизировать общее количество санитаров, которое следует принять на работу.

На первый взгляд математическое описание задачи простое: нужно ввести 7 переменных x_j – количество санитаров, работающих в j-й день недели. Ограничения будут очень простыми: x₁ ≥ 27, x₂ ≥ 23, …, x₇ ≥ 21. Однако, в этом случае целевая функция 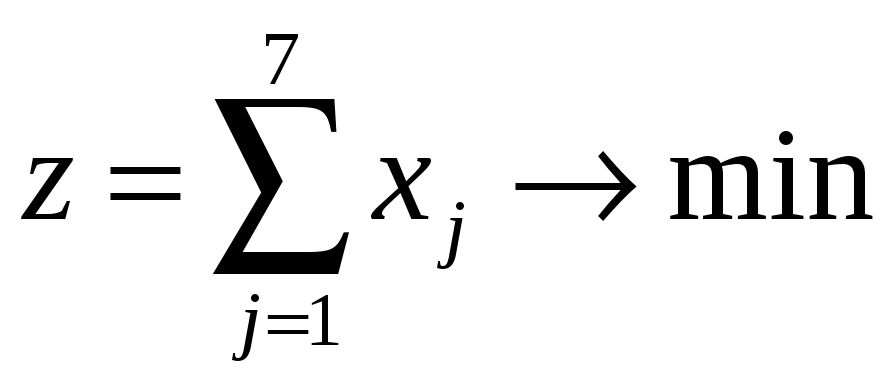не будет показывать, сколько санитаров принято на работу, так как каждый санитар учитывается в ней 5 раз, а отражает только отработанные человеко-дни. Кроме того, при такой постановке в ограничениях никак не учитывается, что переменные x_j связаны между собой, ведь часть людей, работавших в понедельник, будут работать и во вторник, и в среду, и т.д.

Выходом из данной ситуации является понятие того, что не важно сколько людей работает в данный день недели, а важно, сколько людей начинают рабочую неделю с определенного дня недели.

Если обозначить x₁ – количество санитаров, начинающих работу с понедельника (они не будут работать по сб, вс), …, x₇ – количество санитаров, начинающих работу с воскресенья (они не будут работать по пт, сб), получим:

.

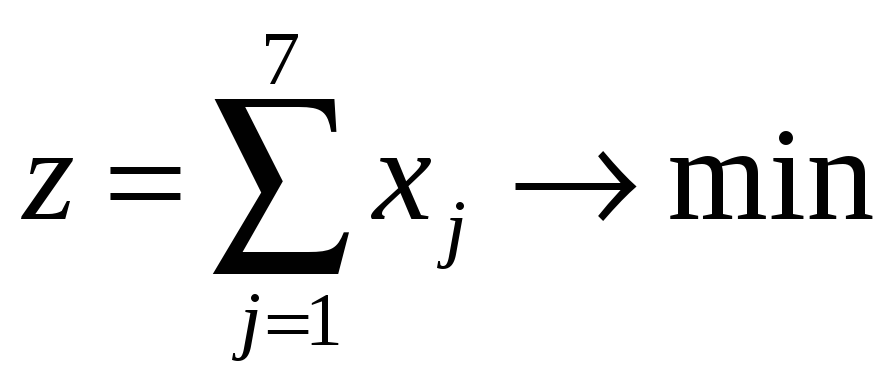Ограничения:

– в пн работают все, кроме тех, кто начинает рабочую неделю со вт (x₂) или со ср (x₃);

– во вт работают все, кроме x₃ и x₄;

.

Заметим, что оптимальное решение этой задачи Z = 35,67, x₁ = 4,67, x₂ = 8,67, x₃ = 0, x₄ = 10,67, x₅ = 0, x₆ = 6,67, x₇ = 5. Это решение нас устроить не может, поскольку по смыслу задачи переменные должны быть целыми. Простое округление переменных дает Z = 37. Однако, при постановке этой задачи как задачи целочисленного программирования (дискретной), можно получить лучшее решение: Z = 36 при x₁ = 6, x₂ = 9, x₃ = 0, x₄ = 10, x₅ = 1, x₆ = 6, x₇ = 4.

Пример 2.4. Динамическая модель принятия решений

Компания производит лодки. Потребность в лодках в каждом квартале составляет: 40, 60, 75, 25. К началу первого квартала компания имеет запас в 10 лодок.

В течение каждого квартала компания может производить до 40 лодок, используя основное рабочее время, затрачивая 400 грн. на 1 лодку. Можно увеличить производство лодок выше 40, используя сверхурочное время, но тогда цена лодки составит 450 грн. Хранение нереализованного на конец квартала запаса лодок обходится компании в 20 грн. за 1 лодку.

Составить производственную программу, минимизирующую затраты на производство и хранение в течение 4 кварталов.

Введем переменные:

4 переменных x_i – количество лодок, произведенных в j-м квартале в основное рабочее время;

4 переменных y_i – количество лодок, произведенных в j-м квартале в сверхурочное время;

4 переменных h_i – количество лодок, нереализованных на конец j-го квартала.

Целевая функция, минимизирующая затраты, имеет вид:

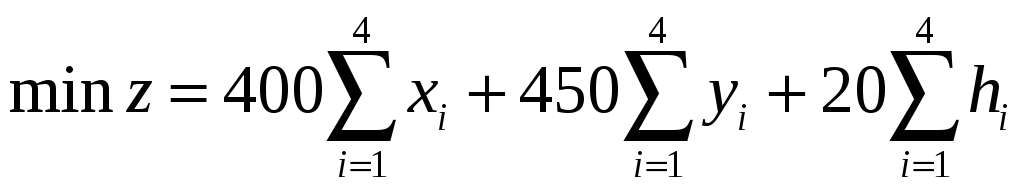
Ограничения по основным производственным мощностям:

ограничения, взаимоувязывающие производство, сбыт и складские запасы:

– запасы на конец первого квартала равны запасам на начало квартала (10) плюс производство в основное (x₁) и сверхурочное (y₁) время в первом квартале, минус объем реализации в первом квартале. Аналогично:

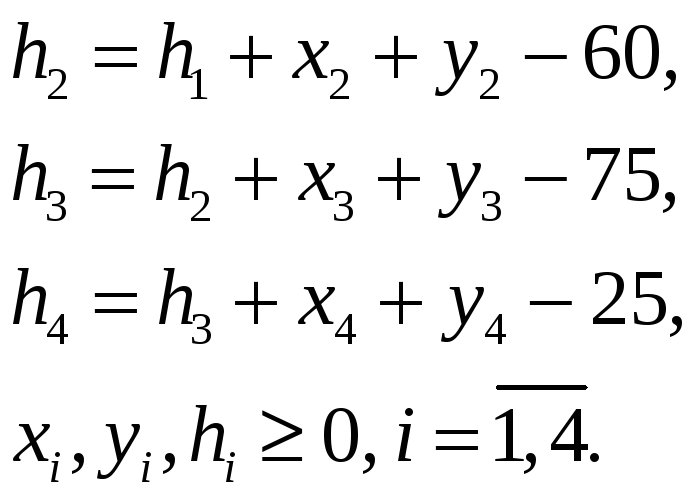
Оптимальным решением данной задачи будет: z = 78 450, , x₄ = 25, y₁ = 0, y₂ = 10, y₃ = 35, y₄ = 0, h₁ = 10, .

Пример 2.5. Задача на раскрой

Для изготовления брусьев длиной 1,2 м, 3 м и 5 м в соотношении 2:1:3 на распил поступают 195 бревен длиной 6 м. Определить план распила, обеспечивающий максимальное число комплектов.

В этой и подобных задачах на раскрой необходимо составить таблицу возможных рациональных вариантов раскроя. В данном случае можно выделить следующие способы распила бревен:

Способ распила, i	Число получаемых брусьев длиной, м
	1,2	3,0	5,0
1	5	-	-
2	2	1	-
3	-	2	-
4	-	-	1

Заметим, что, в принципе, есть и другие варианты распила, например, 1 брус длиной 1,2 м и 1 брус длиной в 3 м, но этот способ не рациональный, поскольку явно хуже имеющегося второго способа. Подобного рода нерациональные способы не рассматриваем.

Обозначим: – число бревен, распиленных i-тым способом (i = 1,2,3,4); x – число комплектов брусьев (которое совпадает с количеством бревен по 3 м).

Учитывая, что все бревна должны быть распилены, а число брусьев каждого размера должно удовлетворять условию комплектности, экономико-математическая модель задачи примет вид:

x₁ + x₂ + x₃ + x₄ = 195 – все бревна должны быть распилены,

5x₁ + 2x₂ = 2x – количество брусьев длиной 1,2 м в 2 раза больше числа комплектов,

x₂ + 2x₃ = x – количество брусьев по 3 м равно числу комплектов,

x₄ = 3x – количество брусьев по 5 м в три раза больше числа комплектов.

.

Часто в задачах на раскрой критерием принятия решения бывает минимизация отходов. Для записи такого критерия в таблице со способами раскроя нужно определить непродуктивные отходы для каждого способа. Для предыдущей задачи отходы для первого способа распила равны нулю, для второго способа – 0,6 м, для третьего – 0, для четвертого – 1 м.

Критерий минимизации отходов в этом случае можно было бы записать так:

.