3.2. Симплекс-метод решения задач линейного программи­рования

Выпишем еще раз задачу линейного программирования в общем виде:

z = с₁x₁ + …+ с_nx_n " min (max) (1)

a₁₁x₁ + …+ a_1nx_n £ (= ³) b₁,

… (2)

a_m1x₁ + …+ a_mnx_n £ (= ³) b_m;

x₁ ³ 0, …, x_n ³ 0. (3)

В матричной форме задача имеет вид (см. п. 2.1):

z = CX " min (max)

AX ≤ (= ³) B (4)

X ≥ 0.

Поскольку, как было показано в п. 3.1 решение задачи линейного программирования находится в одной из крайних (угловых) точек ОДЗ, важным вопросом является изучение не системы неравенств (2), а соответствующей системы уравнений AX = B, решение которой дает угловые точки ОДЗ.

В математике известно, что система из линейных уравнений, имеющих n переменных, имеет единственное решение тогда, когда количество уравнений тоже равно n (числу переменных) и уравнения линейно независимы. (Линейная независимость уравнений обозначает, что ни одно из уравнений нельзя выразить через линейную комбинацию остальных уравнений). Если число линейно независимых уравнений больше числа переменных – система несовместна и решения нет. Если число линейно независимых уравнений меньше числа переменных – решений бесконечное множество.

Следовательно, если уравнения системы АX = B независимы, то система имеет множество решений при n > m и единственное решение при n = m. При решении задачи линейного программирования симплекс-методом всегда будет выполняться n > m, поэтому для получения некоторого одного решения, «лишние» n – m переменных приравниваются нулю.

Если приравнять к нулю n – m произвольных переменных (например, переменные x_m+1, x_m+2, …, x_n) и, решив систему, найти значения оставшихся m переменных (x₁, x₂, …, x_m), то такое решение называется базисным.

Если нулю приравнять некоторые другие n – m переменных – получим другое базисное решение. Любое базисное решение, у которого все переменные неотрицательные называется допустимым базисным решением.

Переменные, которые были приравнены нулю, называются небазисными. Оставшиеся т переменных, значение которых получены из решения системы, называются базисными.

Допустимое базисное решение представляет собой угловую вершину ОДЗ.

Решение задачи симплекс-методом сводится к направленному перебору смежных друг с другом угловых точек, которые представляют собой допустимые базисные решения.

Сформулируем в общем виде алгоритм симплекс-метода:

1: Приведение задачи к стандартной форме. Стандартной формой задачи линейного программирования будем называть задачу, у которой все ограничения записаны как равенства и при этом правые части ограничений неотрицательны.

2: Выделение исходного базисного решения (по возможности из стандартной формы). То есть определение тех переменных n – m переменных, которые приравниваются нулю и нахождение значений оставшихся базисных переменных.

3: Определение, является ли полученное базисное решение оптимальным, если да, то решение окончено, иначе переходим к шагу 4.

4: Определение переменной, которая войдет в базис и переменной, которая из базиса выйдет таким образом, чтобы новое решение было лучше предыдущего. То есть, если текущее базисное решение неоптимально, необходимо определить, какую из базисных переменных приравнять нулю, и какую из небазисных переменных вместо нее включить в базис.

5: Использование эквивалентных преобразований методом Жордана-Гаусса для нахождения нового допустимого базисного решения. Переход к шагу 3.

Чтобы привести задачу линейного программирования к стандартной форме необходимо:

1. Убедиться, что во всех ограничениях правые части b_i неотрицательны. Если есть отрицательные правые части ограничений, такие ограничения нужно умножить на –1 (при этом учесть, что в ограничениях типа  или  знак ограничения изменится на противоположный).

2. К левой части ограничений типа  нужно прибавить новую, дополняющую переменную S, которая уравнивала бы левую и правую часть и показывала бы насколько левая часть ограничения меньше правой.

То есть ограничение

a_i1x₁ + …+ a_inx_n £ b_i

в стандартном виде будет выглядеть так:

a_i1x₁ + …+ a_inx_n + S_i = b_i.

3. Из левой части ограничений типа  нужно вычесть новую, избыточную переменную e, которая уравнивала бы левую и правую часть и показывала бы насколько левая часть ограничения больше правой.

То есть ограничение

a_i1x₁ + …+ a_inx_n  b_i

в стандартном виде будет выглядеть так:

a_i1x₁ + …+ a_inx_n – e_i = b_i.

Дополняющие переменные S и избыточные e будем называть вспомогательными, в то время, как переменные x – основными.

Чтобы из стандартной формы сразу выделить базисное решение, необходимо в качестве базисных переменных выбрать те m переменных, каждая из которых встречается только в одном из уравнений и включена в него с коэффициентом, равным единице.

Действительно, рассмотрим систему ограничений типа £, состоящую для определенности из трех уравнений и четырех переменных:

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + a₁₄x₄ £ b₁,

a₂₁x₁ + a₂₂x₂ + a₂₃x₃ + a₂₄x₄ £ b₂,

a₃₁x₁ + a₃₂x₂ + a₃₃x₃ + a₃₄x₄ £ b₃.

В стандартном виде эта система будет выглядеть так:

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ + a₁₄x₄ + S₁ = b₁,

a₂₁x₁ + a₂₂x₂ + a₂₃x₃ + a₂₄x₄ + S₂ = b₂,

a₃₁x₁ + a₃₂x₂ + a₃₃x₃ + a₃₄x₄ + S₃ = b₃.

Имеем систему из трех уравнений и семи переменных. Среди всех переменных нужно выбрать только три базисных. Возьмем в качестве базисных переменные S₁, S₂, S₃ (каждая из них входит только в одно из уравнений и имеет коэффициент 1). Тогда остальные переменные (x₁, x₂, x₃, x₄) – небазисные и равны нулю. В этом случае базисное решение очевидно:

S₁ = b₁,

S₂ = b₂,

S₃ = b₃.

Если же в качестве базисных переменных мы взяли другие, например, x₁, x₂, x₃, тогда небазисными были бы переменные x₄, S₁, S₂, S₃, но в этом случае базисное решение было бы не очевидным, так как для его получения необходимо было бы решить систему:

a₁₁x₁ + a₁₂x₂ + a₁₃x₃ = b₁,

a₂₁x₁ + a₂₂x₂ + a₂₃x₃ = b₂,

a₃₁x₁ + a₃₂x₂ + a₃₃x₃ = b₃.

Таким образом, в качестве исходных базисных переменных в задачах с ограничениями  удобно брать переменные S₁, …, S_n.

Реализацию алгоритма симплекс-метода проиллюстрируем на следующем примере.

Пример 3.2. Мебельная фабрика может производить шкафы, столы, стулья. При изготовлении мебели используются древесина, труд рабочих на столярном и отделочном участках. Необходимое количество ресурсов для изготовления шкафов, столов и стульев приведено в таблице:

Таблица 3.1 – Исходные данные к примеру 3.2

Ресурсы	Шкаф	Стол	Стул
Древесина	8 м2	6 м2	1 м2
Отделочные работы	4 часа	2 часа	1,5 часа
Столярные работы	2 часа	1,5 часа	0,5 часа

В распоряжении фабрики ежедневно имеется 48 м² древесины, 20 часов времени на участке отделки, 8 часов на столярном участке. Известно также, что потребность в шкафах и стульях неограниченна. Однако не более 5 столов может быть продано ежедневно. Цены реализации продукции следующие: шкаф – 60 у.е., стол – 30 у.е., стул – 20 у.е.

Мебельная фабрика хотела бы использовать имеющиеся ресурсы наилучшим образом, приносящим наивысший доход.

Построим математическую модель. Обозначим х₁ – количество производимых шкафов, х₂ – число столов, х₃ – количество стульев.

Задача линейного программирования примет вид:

1) Целевая функция

2) Система ограничений

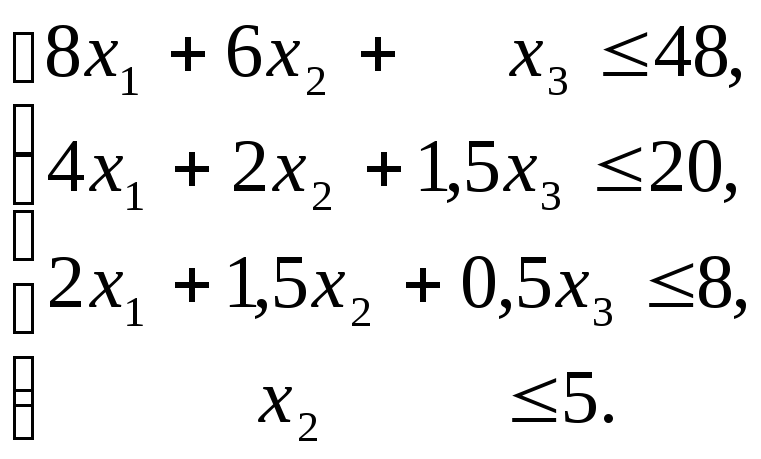
3) Ограничения на знак переменных

х₁, х₂, х₃ 0 .

Преобразуем модель к стандартной форме:

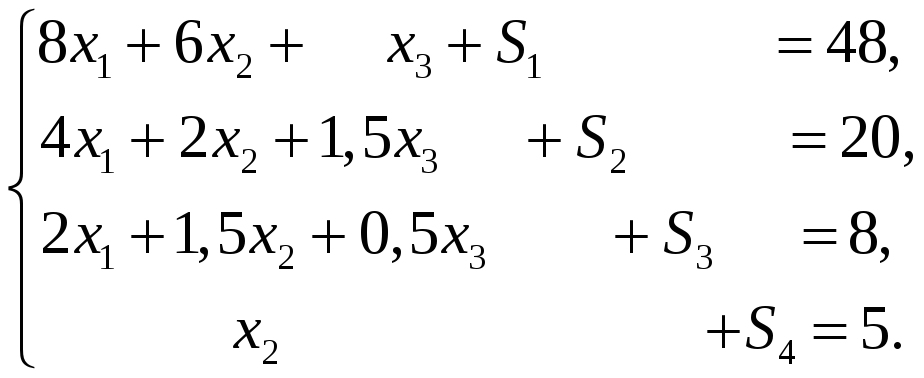(5)

В качестве исходного базиса, очевидно, удобно выбрать переменные S₁, S₂, S₃, S₄, так как очевидно базисное решение:

S₁ = 48, S₂ = 20, S₃ = 8, S₄ = 5.

Говорят, что векторы S₁, S₂, S₃, S₄ образуют базис системы (5)

S₁, S₂, S₃, S₄

Дальнейшие шаги алгоритма симплекс-метода (шаг 3, 4, 5) удобно представить в специальной таблице, называемой симплекс-таблицей.

Построим первую симплекс-таблицу. В первом столбце укажем переменные, образующие базис, во втором столбце (c_j) – коэффициенты целевой функции, при переменных, входящих в базис. В третьем столбце (b_i) – правые части ограничений. В остальных столбцах (x₁, x₂, …, S₄) записываются коэффициенты целевой функции и коэффициенты в ограничениях при соответствующих переменных.

Последняя строка симплекс-таблицы () особая. Она получается из целевой функции следующим образом. В целевой функции все переменные переносятся в левую часть. Получается . Полученные коэффициенты и правая часть целевой функции (0) записывается по аналогии с коэффициентами ограничений: в столбце b_i – правая часть целевой функции, которая изначально равна нулю, в остальных столбцах – обратные значения коэффициентов целевой функции (–с_j) при соответствующих переменных.

Таким образом, исходная симплекс-таблица имеет вид:

Таблица 3.2 – Исходная симплекс-таблица к примеру 3.2

Базис	cj		х1	х2	х3	S1	S2	S3	S4	с.о.
			60	30	20	0	0	0	0
S1	0	48	8	6	1	1	0	0	0	48:8 = 6
S2	0	20	4	2	3/2	0	1	0	0	20:4 = 5
S3	0	8	2	3/2	1/2	0	0	1	0	8:2 = 4
S4	0	5	0	1	0	0	0	0	1	–
		0	-60	-30	-20	0	0	0	0	max

Заметим, что столбец отражает не только правые части ограничений, он также показывает значение базисных переменных S₁, …, S₄. (Напомним, что значение небазисных переменных х₁, х_2, х₃ равно нулю.) Тот же столбец в строке целевой функции отражает значение целевой функции при данном базисном решении. Ведь, действительно, целевая функция Z при х₁ = х₂ = х₃ = 0, тоже равна нулю.

Последняя строка таблицы называется строкой целевой функции или индексной строкой.

Признаком оптимальности в задаче на максимум является наличие в индексной строке всех неотрицательных значений. В нашем примере индексная строка содержит отрицательные элементы (–60, –30, –20). Следовательно, текущее базисное решение неоптимально и его нужно улучшать.

В случае если решается задача на минимум, можно использовать один из двух вариантов:

1) умножить целевую функцию на –1 и решать задачу не на минимум, а на максимум;

2) признаком оптимальности в задаче на минимум считать наличие в индексной строке всех неположительных значений. Так, если бы данная задача 3.2 ставила минимизацию целевой функции, то текущее базисное решение было бы оптимальным (в строке не положительных значений).

Определив, что текущее базисное решение неоптимально, нужно выяснить какую из небазисных переменных х₁, х_2, х₃ нужно включить в базис. Коэффициент –60 в индексной строке показывает, что при введении в базис переменной x₁ в базис со значением 1, целевая функция улучшится на 60 единиц. При введении в базис x₂ со значением 1, ЦФ улучшится на 30 единиц. При введении в базис x₃ – на 20.

Наилучший прирост целевой функции дает введение в базис переменной x₁.

Таким образом, при решении задачи на максимум в базис войдет та переменная, которая имеет отрицательное значение в индексной строке и из всех отрицательных значений, оно наибольшее по модулю.

Рассуждая аналогично, при решении задачи на минимум, используя вариант 2), в базис войдет та переменная, которая имеет положительное значение в индексной строке и из всех положительных значений, оно наибольшее.

Столбец с переменной, которая собирается войти в базис называется разрешающим столбцом. В нашей задаче разрешающим, является столбец х₁.

Выясним, какая переменная выйдет из базиса и с каким значением переменная х₁ войдет в базис. Эти задачи взаимосвязанные. Вывести из базиса нужно такую переменную, чтобы став равной нулю, она не привела к тому, что какая-то из остальных базисных переменных станет отрицательной (недопустимой). Нужно, чтобы приравняв одну из базисных переменных нулю, остальные базисные переменные, в том числе и та, которая входит в базис, оставались неотрицательными.

Рассмотрим текущую систему уравнений при введении x₁ в базис:

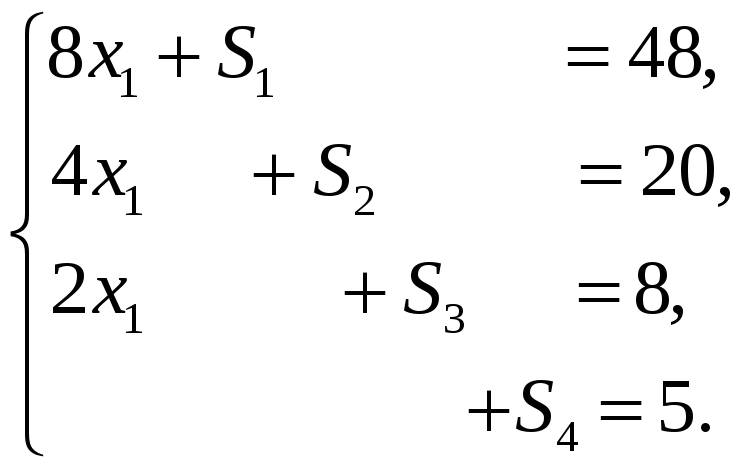
Предположим, что базис покинет S₁, тогда если S₁ = 0, из первого уравнения x₁ = 48/8 = 6. То есть x₁ должно войти в базис со значением 6.

Однако, это невозможно: подставим x₁ = 6 во второе уравнение, получим 4∙6 + S₂ = 20  S₂ = –4. Но S₂ по определению не может быть отрицательной. Такой базис недопустимый.

Предположим, что базис покинет S₂, тогда если S₂ = 0, из второго уравнения x₁ = 20/4 = 5. То есть x₁ должно войти в базис со значением 5.

Однако, и это невозможно: подставим x₁ = 5 в третье уравнение, получим 2∙5 + S₃ = 8  S₂ = –2. Но S₃ не может быть отрицательной.

Пусть, базис покинет S₃, тогда если S₃ = 0, из третьего уравнения x₁ = 8/2 = 4. Подставив это значение в первое уравнение, получим, 32 + S₁ = 48  S₁ = 16, что допустимо. Подставив это значение во второе уравнение, получим, 16 + S₂ = 20  S₂ = 4, что тоже допустимо. На значение переменной S₄ значение переменной x₁ не влияет, так как x₁ не входит в четвертое уравнение (входит с коэффициентом ноль).

Заметим, что переменная S₄ не может покинуть базис, так как иначе при S₄ = 0 в четвертом уравнении получим противоречие 0 = 5.

Таким образом, для определения того, какая переменная покинет базис, необходимо рассчитать отношения , где b_i – значения коэффициентов правых частей ограничений в столбце b_i симплекс-таблицы, a_ij – значения разрешающего столбца ( j):

48:8 = 6; 20:4 =5; 8:2 = 4.

Данные отношения называются симплексными отношениями. Они записываются в последнем столбце симплекс-таблицы (с.о.). Рассчитывать имеет смысл только неотрицательные симплексные отношения. Отрицательное симплекс-отношение обозначает, что ни при каком допустимом значении входящей в базис переменной нельзя обеспечить непротиворечивое равенство в том ограничении, в котором переменная покидает базис.

Из полученных неотрицательных симплексных отношений выбираем наименьшее. В нашем случае наименьшее симплексное отношение получается в строке 3) S₃, следовательно, переменная S₃ покинет базис, а данная строка будет разрешающей строкой.

Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки также называется разрешающим элементом.

Вместо S₃ в третью строку новой симплекс-таблицы войдет х₁ с коэффициентом c_j равным 60, т.к. 60 – коэффициент целевой функции при x₁.

Разрешающий столбец , который сейчас имеет вид

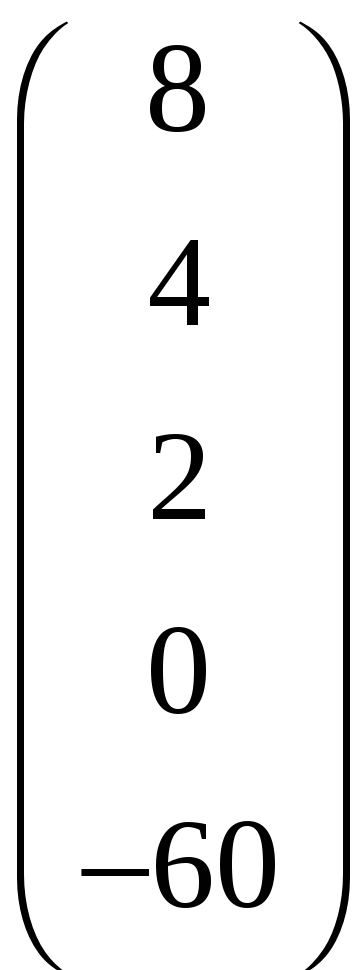, нужно преобразовать к виду ,

то есть к такому же виду, какой имел столбец S₃ в таблице 3.2.

Воспользуемся методом Жордана-Гаусса.

На месте разрешающего элемента нужно получить единицу. Следовательно, всю разрешающую строку (кроме столбца с_j) нужно разделить на разрешающий элемент.

Строку 3) х₁ разделим на 2, она примет вид:

3)

4

1

3/4

1/4

0

0

1/2

0

Строку 4) S₄ переносим из первой симплекс-таблицы во вторую без изменений, так как в столбце х₁ уже находится нулевой элемент.

Строку 1) S₁ необходимо обновить таким образом, чтобы в столбце х₁ был коэффициент 0. Для этого из строки S₁ следует вычесть строку х₁, умноженную на 8.

1) S1 8х1 S1-8х1	48	8	6	1	1	0	0	0
	-32	-8	-6	-2	0	0	-4	0
	16	0	0	-1	1	0	-4	0

Со строкой 2) S₂ поступаем аналогично (из строки S₂ следует вычесть 4 строки ):

2) S2 4х1 S2-4х1	20	4	2	3/4	0	1	0	0
	-16	-4	-3	-1	0	0	-2	0
	4	0	-1	1/2	0	1	-2	0

Для обновления строки к ней необходимо прибавить 60 строк .

	0	-60	-30	-20	0	0	0	0
	240	60	45	15	0	0	30	0
	240	0	15	-5	0	0	30	0

Заполним вторую симплекс-таблицу.

Таблица 3.3 – Вторая симплекс-таблица к примеру 3.2

Базис	cj		х1	х2	х3	S1	S2	S3	S4	с. о.
			60	30	20	0	0	0	0
1) S1	0	16	0	0	-1	1	0	-4	0	–
2) S2	0	4	0	-1	1/2	0	1	-2	0	8
3) х1	60	4	1	3/4	1/4	0	0	1/2	0	16
4) S4	0	5	0	1	0	0	0	0	1	–
		240	0	15	-5	0	0	30	0	max

Из таблицы видно, что полученное новое базисное решение стало лучше предыдущего: выпуск 4 шкафов (x₁ = 4) позволяет получить уже 240 у.е. дохода. Однако, это решение не оптимальное. Это видно из индексной строки таблицы: требование оптимальности не выполнено, так как имеется отрицательный элемент (–5). Будем улучшать план. В качестве разрешающего столбца теперь выбираем столбец , так как он содержит отрицательный элемент (–5). Разрешающую строку выберем, как и ранее, используя симплексное отношение (16 не делим на (-1), так как отрицательные значения не рассматриваются):

4: = 8; 4: = 16.

Из полученных симплексных отношений выбираем наименьшее, следовательно, в качестве разрешающей строки выбираем вторую строку. Переменная х₃ вытесняет S₂ из базиса. Вновь используем метод Жордана-Гаусса, добиваемся того, чтобы столбец х₃ имел вид:

.

Обновляем в табл. 3.3. строки 1) S₁, 2) х₃, 3) х₁, 5) . Значения разрешающей строки 2) S₂ умножаются на 2, т.к. разрешающий элемент 1/2, а надо иметь разрешающим элементом 1, и вместо переменной S₂ записывается переменная :

2) х3

8

0

-2

1

0

2

-4

0

Для обновления строки 1) S₁ необходимо к ней прибавить одну разрешающую строку , так как вместо элемента –1 нужно получить значение, равное 0.

1) S1 S1+х3	16	0	0	-1	1	0	-4	0
	8	0	-2	1	0	2	-4	0
	24	0	-2	0	1	2	-8	0

Аналогично для строки 3) , вместо элемента 1/4 в обновленной строке должен быть нуль. Значит, от 1/4 надо вычесть 1/4. Из строки х₁ вычитаем 1/4 разрешающей строки:

3)	4	1	3/4	1/4	0	0	1/2	0
	2	0	-1/2	1/4	0	1/2	-1	0
	2	1	5/4	0	0	-1/2	3/2	0

Строка 4) S₄ переписывается без изменений, так как в разрешающем столбце у нее нулевое значение.

Для обновления строки к ней следует прибавить пять разрешающих строк .

Z	240	0	15	-5	0	0	30	0
	40	0	-10	5	0	10	-20	0
	280	0	5	0	0	10	10	0

Заполним итоговую симплекс-таблицу.

Таблица 3.4 – Итоговая симплекс-таблица к примеру 3.2

Базис	cj		х1	х2	х3	S1	S2	S3	S4
			60	30	20	0	0	0	0
1) S1	0	24	0	-2	0	1	2	-8	0
2) х3	20	8	0	-2	1	0	2	-4	0
3) х1	60	2	1	5/4	0	0	-1/2	3/2	0
4) S4	0	5	0	1	0	0	0	0	1
		280	0	5	0	0	10	10	0

В строке целевой функции все коэффициенты при переменных неотрицательны, следовательно, мы нашли оптимальное из допустимых решений. Базис образуют переменные , то есть для получения максимального дохода следует выпускать продукцию и , так как переменная не входит в базис (а значит равна нулю). В столбце имеем оптимальные значения базисных переменных: x₁ = 2, x₃ = 8. Значения вспомогательных переменных S₁ = 24, S₄ = 5 можно интерпретировать следующим образом: 24 м² древесины осталось не использовано, спрос на столы не удовлетворен на 5 единиц. Тот факт, что S₂ = S₃ = 0, говорит о том, что все ресурсы по участку отделки и столярному участку использованы полностью.

Целевая функция нашей задачи имеет вид:

.

Для определения ее максимального значения подставим в нее значения переменных, образующих оптимальное базисное решение:

Это же значение видно в последней симплекс-таблице на пересечении индексной строки и столбца .

Таким образом, наибольший доход 280 у.е. получается при производстве 2 единиц товара (шкафы) и 8 единиц товара (стулья).

Проанализируем полученное решение.

Каждая из вспомогательных переменных S₁, …, S₄ соответствовала одному из ограничений и показывала, насколько левая часть ограничения (фактические затраты ресурсов) меньше правой части (их запаса). Таким образом, в тех ограничениях, где левая часть равна правой (запас ресурсов исчерпан полностью), соответствующая вспомогательная переменная S будет равна нулю. Вспомним, что такое ограничение называется связующим и отражает критический (дефицитный) ресурс.

Запасы ресурсов на участке отделки и столярном участке использованы полностью S₂ = S₃ = 0. Древесина же осталось неиспользованной (S₁ = 24). Если увеличить запас древесины (с 48 до, например, 68), приведет ли это к улучшению решения? Нет. Поскольку она и так осталась лишняя увеличение правой части несвязующего ограничения приведет к тому, что увеличится значение соответствующей вспомогательной переменной (станет S₁ = 44), но оптимальный план не изменится.

Дефицитные же ресурсы являются ценными в том смысле, что их увеличение приведет к возможности улучшения оптимального плана. Оценка ценности данных ресурсов приведена в строке целевой функции : при указанных переменных стоят коэффициенты 10. Эти величины называются теневыми ценами и отражают степень важности ресурса с точки зрения его вклада в оптимальный результат. Теневая цена показывает, насколько изменится значение целевой функции, если изменить правую часть соответствующего ограничения на 1 единицу. Теневые цены рассчитывается только для ресурсов, которые использованы полностью, то есть для связующих ограничений.

В строке целевой функции коэффициент 5 при свободной основной переменной x₂ носит название снижающей оценки и показывает, насколько ухудшится целевая функция, если мы примем решение производить хотя бы 1 стол. Снижающую оценку можно интерпретировать и с другой стороны: она показывает, насколько нужно увеличить цену на столы, чтобы их производство стало выгодно, и они вошли в базис.

Пример 3.3. Решить симплекс-методом задачу:

при ограничениях:

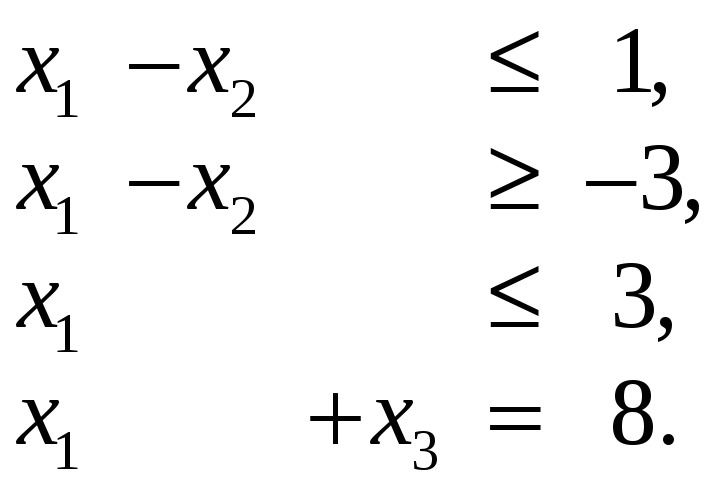
Приводим задачу к стандартному виду: второе ограничение умножаем на –1, чтобы в правой части было положительное значение, и в каждое из ограничений со знаком ≤ вводим добавочную переменную:

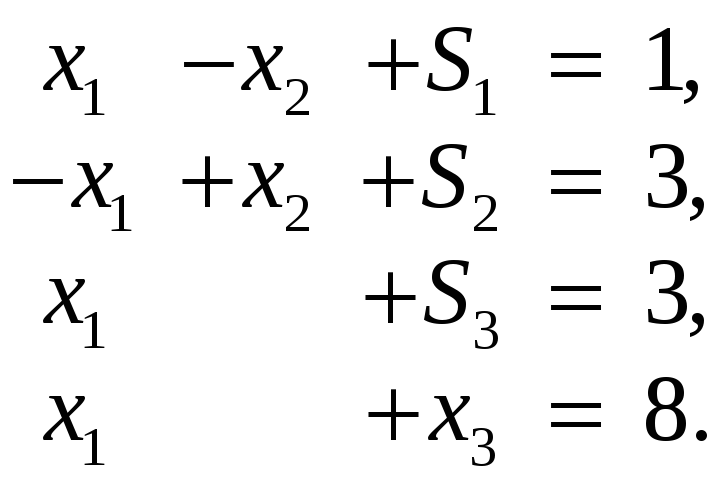
В качестве исходного базиса для каждого ограничения выбираем такую переменную, которая встречается только в этом ограничении и имеет коэффициент 1. Это переменные S₁, S₂, S₃, x₃. Однако, заметим, что переменная x₃ входит в целевую функцию и ее из нее нужно исключить. Выпишем целевую функцию в виде Z – c_j:

Z – 2x₁ – 4x₂ – x₃ = 0.

К этому выражению прибавим четвертое ограничение, чтобы исключить переменную x₃ из целевой функции. Получим:

Z – x₁ – 4x₂ = 8.

Число 8 в правой части полученного выражения отражает значение целевой функции при данном базисе.

Теперь построим симплексные таблицы и решим задачу.

Базис	cj		х1	х2	х3	S1	S2	S3	с. о.
			2	4	1	0	0	0
1) S1	0	1	1	–1	0	1	0	0	–
2) S2	0	3	–1	1	0	0	1	0	3
3) S3	0	3	1	0	0	0	0	1	–
4) x3	1	8	1	0	1	0	0	0	–
		8	–1	–4	0	0	0	0	max

Решение не оптимально, так как есть отрицательные значения в индексной строке. Переменная x₂ должна войти в базис (она имеет наибольшее по модулю отрицательное значение в индексной строке). Покинуть базис должна переменная S₂ (только для нее можно рассчитать неотрицательное симплекс-отношение).

Базис	cj		х1	х2	х3	S1	S2	S3	с. о.
			2	4	1	0	0	0
1) S1	0	4	0	0	0	1	1	0	–
2) x2	4	3	–1	1	0	0	1	0	–
3) S3	0	3	1	0	0	0	0	1	3
4) x3	1	8	1	0	1	0	0	0	8
		20	–5	0	0	0	4	0	max

Видим, что решение улучшилось (при x₂ = 3, x₁ = 8, Z = 20), однако решение не оптимально. Переменную x₁ нужно ввести в базис. Покинет базис S₃, так как у нее минимальное симплексное отношение.

Базис	cj		х1	х2	х3	S1	S2	S3
			2	4	1	0	0	0
1) S1	0	4	0	0	0	1	1	0
2) x2	4	6	0	1	0	0	1	1
3) x1	0	3	1	0	0	0	0	1
4) x3	1	5	0	0	1	0	0	–1
		35	0	0	0	0	4	5

Полученное решение (S₁ = 4, x₁ = 3, x₂ = 6, x₃ = 5) – оптимальное. При этом целевая функция принимает максимальное значение 35. Связующими являются второе, третье и четвертое ограничения (четвертое ограничение связующее, поскольку изначально было равенством, второе и третье – поскольку соответствующие переменные S₂ и S₃ не в базисе и равны нулю).

Числа 4 и 5 в индексной строке отражают теневые цены связующих ограничений 2 и 3 и показывают, насколько могло бы измениться решение (значение целевой функции), если изменить правую часть соответствующего ограничения на 1 единицу.