Тема 2 оптимизационные экономико-математические модели
2.1. Понятие оптимизационной модели
Принятие решения при управлении экономической системой требует разработки некоторой совокупности действий, и, как правило, существует множество вариантов таких действий. Если из всех вариантов действий можно по некоторому критерию выбрать наилучший вариант, то есть такой вариант, который лучше всего приближает к цели управления экономической системой, то задача выбора наиболее эффективного варианта действий называется оптимизационной.
Под критерием оптимальности будем понимать показатель, характеризующий предельную меру эффекта, получаемого от реализации принятого решения, служащий для сравнения различных вариантов решения и выбора наилучшего из них.
Критерий оптимальности может меняться в зависимости от того, какая ставится задача. Так, если на предприятии намечается внедрить систему мер по экономии ресурсов, показателем эффективности будет сумма сэкономленных ресурсов, однако это может привести к увеличению количества брака. С другой стороны, если показателем эффективности рассматривать количество брака, возможно, решением задачи может оказаться необходимость повышенного расхода ресурсов.
Оптимизационные задачи, содержащие несколько целей, которые могут противоречить друг другу, называются многокритериальными задачами.
Оптимизационной моделью называется модель, которая включает в себя:
1. Функцию переменных принятия решений, которая является критерием принятия решений (критерием оптимальности) и которая максимизируется или минимизируется. Такая функция называется целевой функцией (ЦФ) или функцией цели.
Примером целевой функции может быть: максимизация прибыли, объема продаж, сэкономленных ресурсов; минимизация затрат, времени, расстояния.
2. Систему ограничений на значение переменных принятия решений в виде системы уравнений или неравенств.
Почему нельзя до бесконечности увеличить объем продаж, максимизируя данный критерий? Потому что действует ряд ограничений: по спросу на продукцию, по количеству ресурсов, имеющихся в распоряжении предприятия, по производственным мощностям и т.п.
Почему нельзя до нуля уменьшить затраты на производство? Потому что тогда ничего не будет производиться. Поэтому нужно ввести систему ограничений: на объем производимой продукции, на обеспечение должного уровня качества продукции, на технологические особенности производства (например, на предприятиях с непрерывным циклом производство нельзя «приостановить»).
3. Ограничения на знак переменных. Для любой переменной принятия решения xj ограничение на знак определяет, должна ли данная переменная быть всегда неотрицательной (xj ≥ 0) или же она может быть неограниченной на знак (то есть принимать любые, как положительные, так и отрицательные значения).
В подавляющем большинстве экономических задач суть переменных принятия решения определяется так, что отрицательные значения переменных не имеют смысла: нельзя произвести (перевести, продать) отрицательное количество продукции, построить (установить, разместить) отрицательное число объектов и т.п. Поэтому вводится ограничение на знак переменных.
В соответствии с данным определением оптимизационная модель в общем виде выглядит так:
z = f(x1, …, xn) min (max)
при ограничениях:
g1(x1, …, xn) (= ) b1,
g2(x1, …, xn) (= ) b2,
…
gm(x1, …, xn) (= ) bm;
и ограничениях на знак переменных:
x1 0, …, xn 0.
Если и целевая функция f(x1, …, xn) и все функции ограничений g1, …, gm являются линейными, то оптимизационная модель называется линейной.
Задача линейной оптимизации (или линейного программирования) в общем виде выглядит так:
z = с1x1 + …+ сnxn min (max) (1)
a11x1 + …+ a1nxn (= ) b1,
… (2)
am1x1 + …+ amnxn (= ) bm;
x1 0, …, xn 0. (3)
Константы с1,
…, сn
– называются коэффициентами
целевой функции,
которые можно обозначить вектором-строкой
C
= (с1,
…, сn).
Константы aij
называются технологическими
коэффициентами.
Технологические коэффициенты образовывают
прямоугольную матрицу A
={aij}m×n,
имеющую m
строк и n
столбцов, которая называется матрицей
технологических коэффициентов.
Константы b1,
…, bm
называются правыми частями ограничений
и образовывают вектор-столбец
.
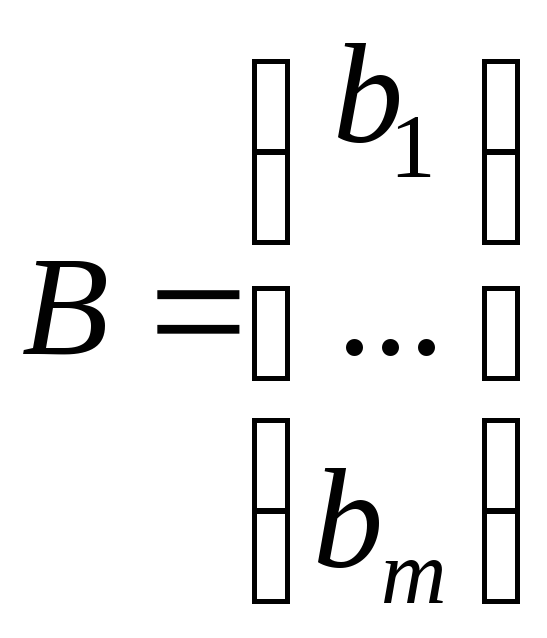Если переменные принятия решений также
представить в виде вектора-столбца
,
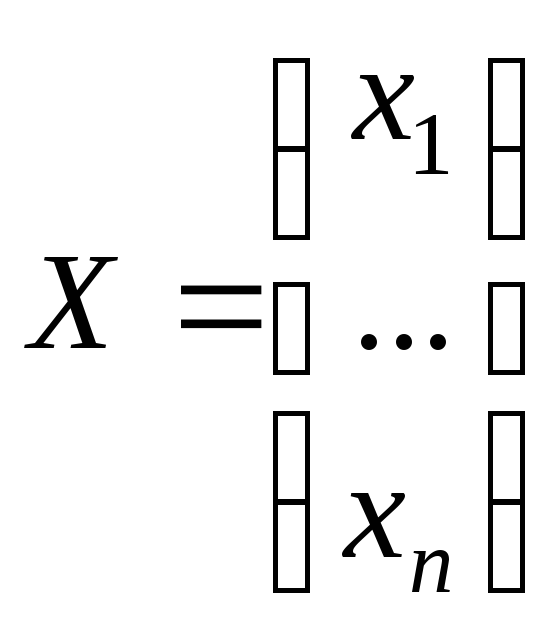то задачу (1)-(3) можно представить в
матричной форме:
z = CX min (max)
AX ≤ (= ) B (4)
X ≥ 0.
Суть задачи оптимизации состоит в том, что из всех возможных значений переменных Х, удовлетворяющих ограничениям (2)-(3) необходимо выбрать такое, которое давало бы наилучшее значение целевой функции (1).
При описании экономических процессов задачей линейного программирования необходимо, чтобы реальные процессы удовлетворяли следующим требованиям:
пропорциональности и аддитивности (по вкладу переменных в функции f, g1, …, gm );
непрерывности (значения переменных могут быть дробными);
детерминированности (все параметры сj, aij и bi должны быть известны и представлены в виде констант);
неотрицательности переменных.
Каждое конкретное решение Х (являющееся набором значений переменных x1, … xn) называется точкой.
Множество всех точек, удовлетворяющих ограничениям (2) и (3), называется областью допустимых значений (ОДЗ).
Любая точка, которая не входит в ОДЗ, называется недопустимой точкой.
Оптимальным решением называется такая точка из ОДЗ, которая дает наилучшее значение целевой функции (1).
Рассмотрим некоторые примеры описания экономических задач в виде моделей линейной оптимизации.