6.2. Метод множителей Лагранжа

Решение классической задачи математического программирования, сводится к нахождению условного экстремума. То есть нужно найти экстремум функции f(x₁, …, x_n), а на переменные накладываются условия

g₁(x₁, …, x_n) = 0,

…

g_m(x₁, …, x_n) = 0,

причем m < n.

Для решения таких задач разработан специальный метод множителей Лагранжа. Суть метода в следующем.

Составляется функция Лагранжа

L(x₁, …, x_n, ₁, …, _m) = f(x₁, …, x_n) + ₁g₁(x₁, …, x_n) + … + _mg_m(x₁, …, x_n) =

= f(x₁, …, x_n) + ,

где ₁, …, _m – первоначально неизвестные константы, которые носят называние множителей Лагранжа. Функция Лагранжа исследует на безусловный экстремум. Для этого находятся первые производные по всем переменным и решается система уравнений:

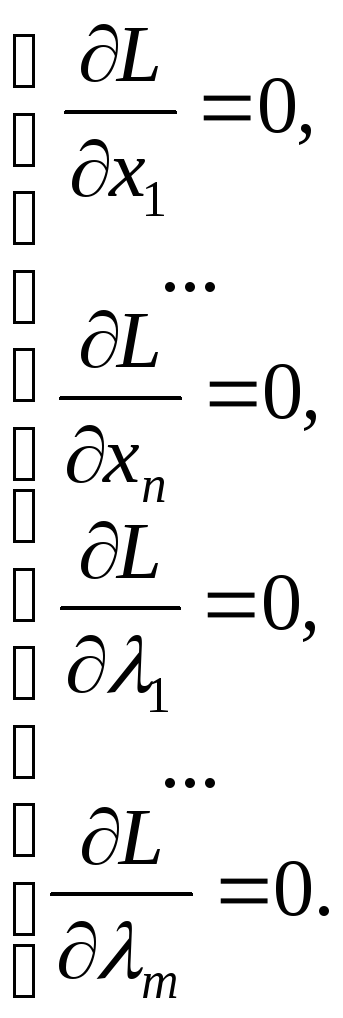
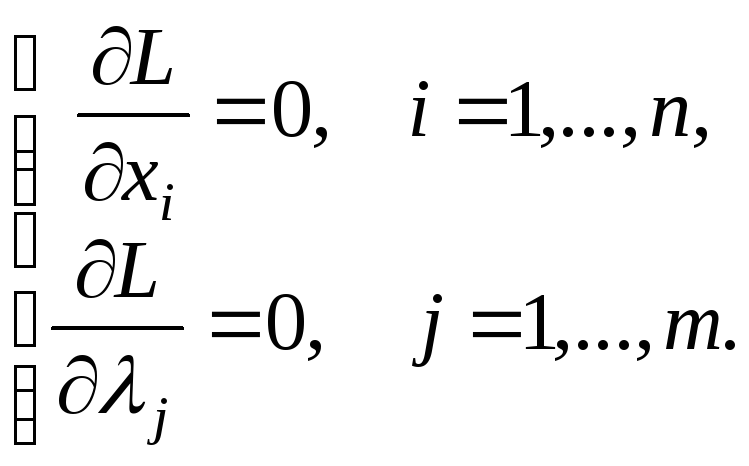
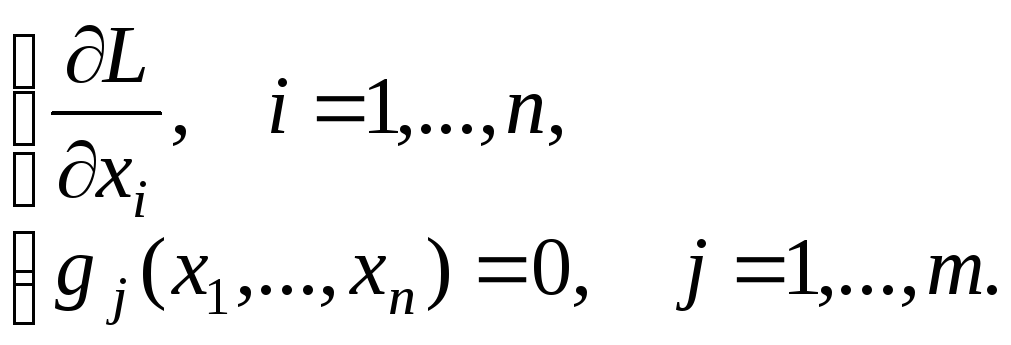  (15)

Заметим, что поскольку _j константа, .

Для каждого решения этой системы (x₁, …, x_n, ₁, …, _m) нужно исследовать знак дифференциала второго порядка функции Лагранжа в этой точке

d²L(x₁, …, x_n, ₁, …, _m) = .

При этом на дифференциалы dx_i, dx_j налагаются m различных соотношений из условий

g₁(x₁, …, x_n) = 0,

… (16)

g_m(x₁, …, x_n) = 0.

Если d²L(x₁, …, x_n, ₁, …, _m) < 0, то (x₁, …, x_n, ₁, …, _m) – точка условного максимума, если d²L(x₁, …, x_n, ₁, …, _m) > 0, то (x₁, …, x_n, ₁, …, _m) – точка условного минимума.

На самом деле, если решением системы (15) являются несколько точек, то достаточно найти значение ЦФ в этих точках и выбрать из них наибольшее и наименьшее. Тогда исследовать знак второго дифференциала необязательно. Впрочем, даже если решением системы (15) является единственная точка (x₁, …, x_n, ₁, …, _m), можно подставить в ЦФ произвольные точки, лежащие в ее окрестности и удовлетворяющие системе (16). Если значение ЦФ меньше, чем в точке (x₁, …, x_n, ₁, …, _m) – имеем условный максимум, если больше – условный минимум.

Пример 6.2.

Запишем ограничение в виде и составим функцию Лагранжа:

L(x₁, x₂, ) = .

Находим для этой функции частные производные первого порядка:

,

,

_.

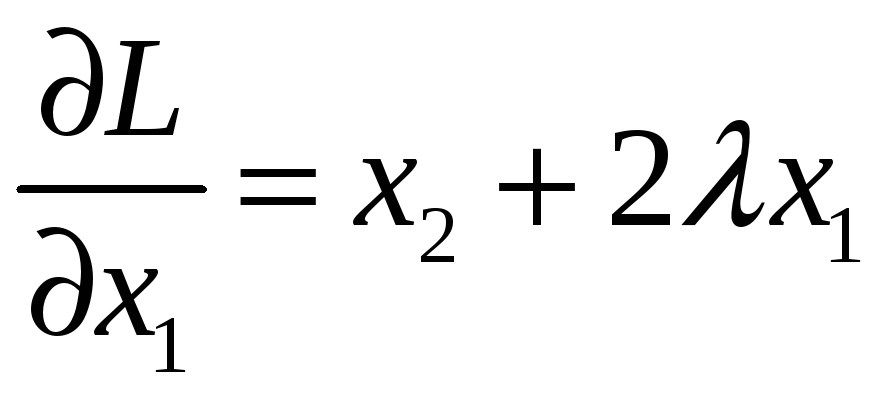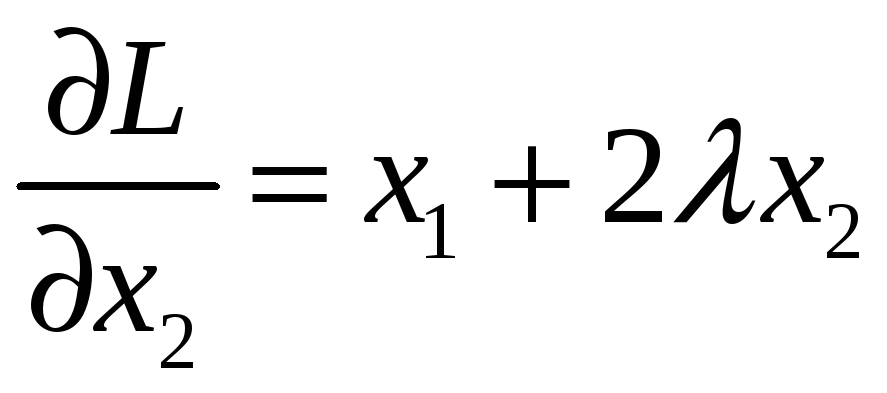Приравнивая каждую производную нулю, получаем систему уравнений:

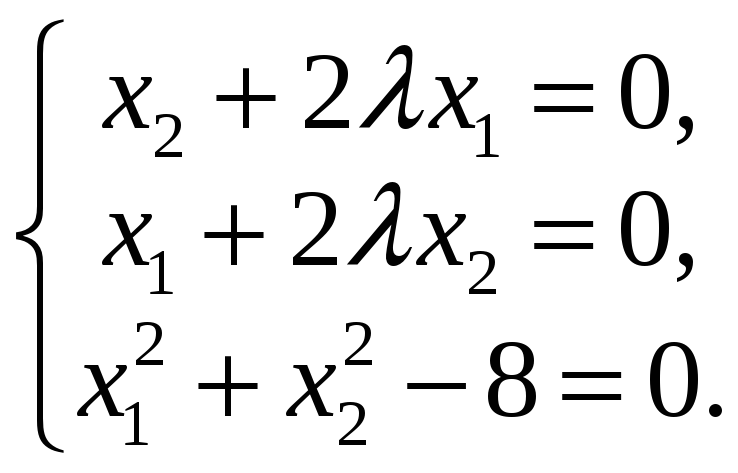
Решим эту систему. Если x₁ = 0, то x₂ = 0 (из 1-го уравнения). Тогда , то есть, не выполняется третье уравнения. Значит x₁  0 и из 1-го уравнения 2 = –x₂/x₁.

Подставим это во второе уравнение:

Отсюда .

Подставим это в третье уравнение:

, то есть , x₁ = 2. Но x₂ = x₁. Получаем четыре точки: (2; 2), (2; –2), (–2; 2), (–2; –2).

Поскольку экстремальных точек несколько, для определения какая из них максимальная, а какая минимальная найдем в этих точках значение ЦФ и выберем наибольшее и наименьшее:

f(2; 2) = 4; f(2; –2) = –4; f(–2; 2) = –4; f(–2; –2) = 4.

То есть, f_max = 4 достигается в точках (2; 2), (–2; 2), f_min = –4 – в точках (–2; 2), (2; –2).

Множитель Лагранжа  = 0,5 в точках минимума и  = –0,5 в точках максимума (например, из 1-го уравнения). Эти значения имеют такую же интерпретацию, как и теневые цены в задаче линейного программирования. Они отличны от нуля, только если ограничение связующее и показывают, как изменится оптимальное значение ЦФ при изменении правой части ограничения на 1 единицу.

Решим методом множителей Лагранжа задачу примера 6.1:

.

Функция Лагранжа имеет вид:

L(x₁, x₂, ) = .

Откуда, найдя первые производные, получаем систему:

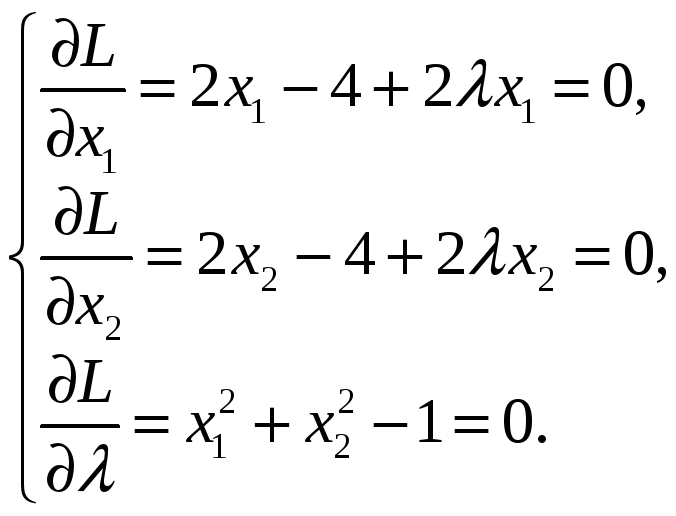
Из 1-го уравнения  . (Заметим, что знаменатель не равен нулю, то есть   –1, иначе из 1-го уравнения следовало бы ).

Аналогично, из второго уравнения  .

Подставим эти значения в третье уравнение. Получим:

.

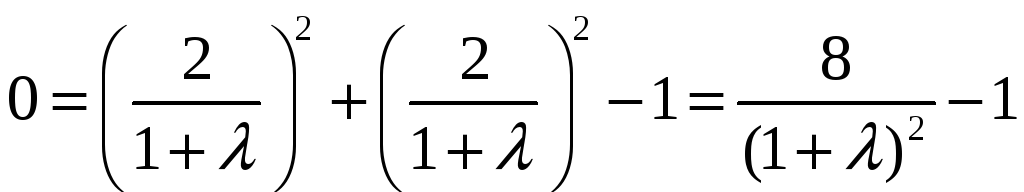Отсюда получаем квадратное уравнение:

= 8  1+  =   = – 1.

Подставляя эти значения в выражения для x₁ и x₂, получим две пары точек:

;

;

Эти же точки мы получили, применив графический метод (рис. 6.1). Подставив эти точки в целевую функцию, определяем, что в точке 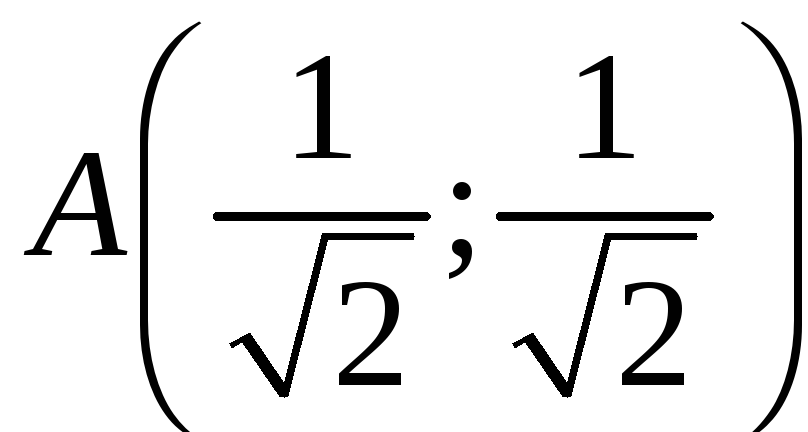– минимум: f_min 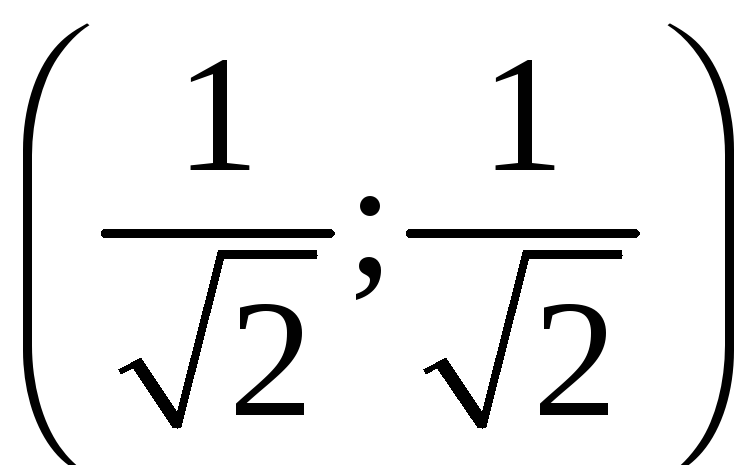= 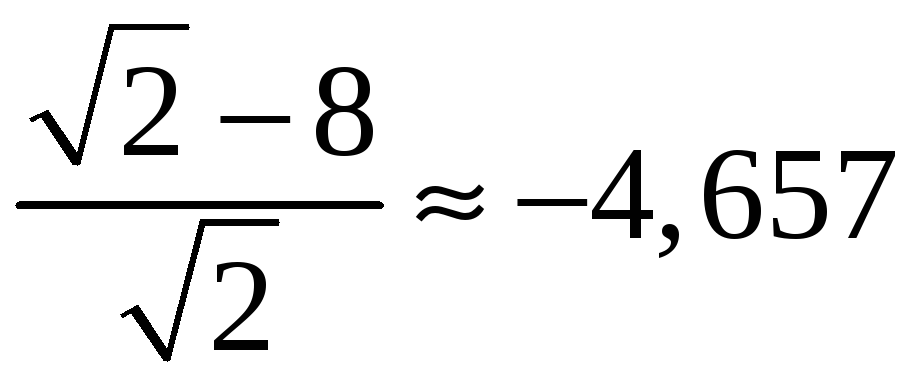. В точке 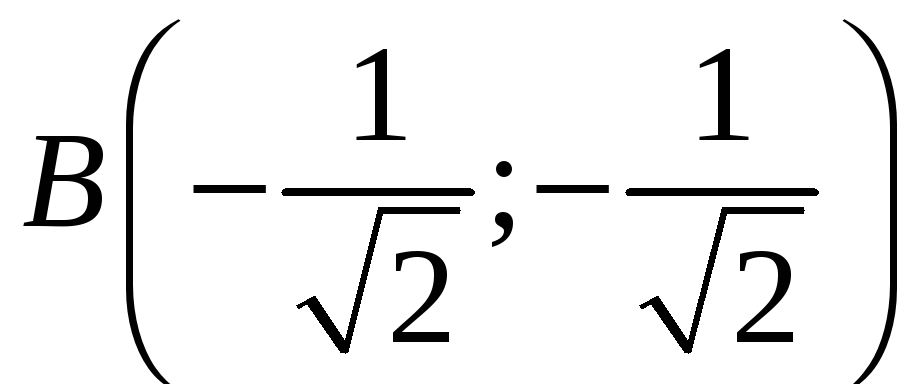– максимум: f_max = .

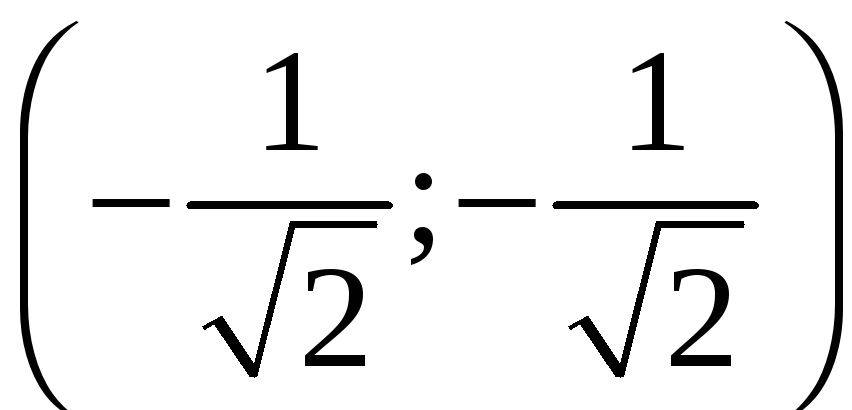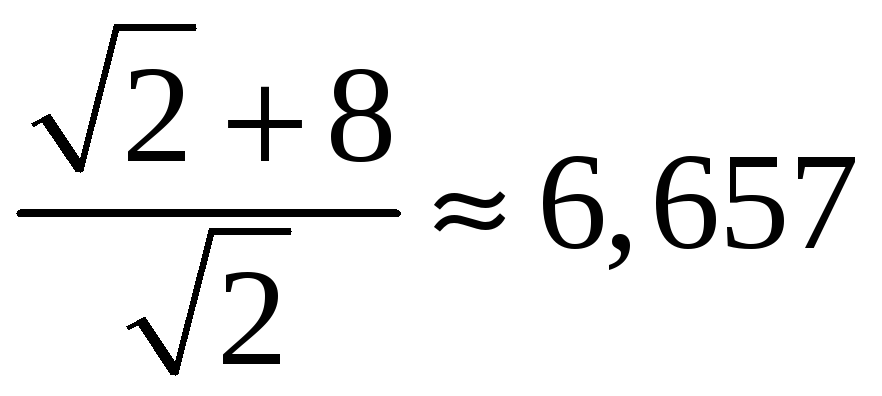Так называемый обобщенный метод множителей Лагранжа можно применить и для решения некоторых задач нелинейного программирования.

В этом случае ограничения на знак переменных задачи нелинейного программирования рассматриваются наравне с обычными ограничениями, то есть включаются в m ограничений задачи (14).

Основная идея метода в следующем.

Шаг 1. На наличие экстремумов исследуется только ЦФ без учета ограничений, то есть решается задача f(x₁, …, x_n)  max(min). Полученное решение проверяется на допустимость: подставляется в ограничения. Если все ограничения удовлетворяются, то задача решена. В этом случае имеет место решение, которое находится во внутренней точке ОДЗ, как показано на рис. 6.2 б – то есть все ограничения оказываются избыточными.

Иначе, если хотя бы одно из ограничений не удовлетворяется, решение задачи будет находиться в крайней точке ОДЗ, а это значит, что некоторые (как минимум одно) ограничения будут выполняться как строгое равенство. В этом случае можно применить метод множителей Лагранжа. Дальнейшие действия такие: полагают k = 1 и переходят к шагу 2.

Шаг 2. Берутся любые k ограничений задачи и преобразовываются в равенства (путем добавления добавочной или избыточной переменной S или e) и оптимизируется ЦФ при наличии k ограничений методом множителей Лагранжа. Если оптимальное решение является допустимым по отношению к остальным решениям задачи, оно запоминается (оно является локальным оптимумом). На этом часто вычислительную процедуру останавливают, поскольку локальный оптимум часто дает приемлемый результат, однако, могут существовать другие локальные оптимумы лучше этого. Поэтому, взяв другие k ограничений исходной задачи можно попытаться найти другие локальные оптимумы и выбрать из них наилучший.

Если оптимальное решение является недопустимым, берутся другие k ограничений и шаг 2 повторяется. Если же, перебрав все возможные комбинации из k ограничений, решения получаются такие, что не удовлетворяют всем ограничениям исходной задачи, полагают k = k +1 и повторяют шаг 2 для большего на 1 количества ограничений.

Шаг 3. Если k = m, а допустимого решения не найдено, то задача не имеет решений.

При всех достоинствах, недостатком этой вычислительной процедуры является то, что она не гарантирует получения глобального оптимума даже в тех случаях, когда задача имеет единственное оптимальное решение. Исходя из алгоритма, вычислительную процедуру следует завершить при нахождении хотя бы одно допустимого локального оптимума, однако теоретически может быть лучшее решение, если задействовать большее число ограничений. Но ввиду сложности вычислительных процедур, перебрать все комбинации ограничений невозможно, ведь даже при трех ограничениях в этом случае шаг 2 придется проходить 7 раз, а при пяти ограничениях – 31 раз. Поэтому на практике часто довольствуются первым найденным локальным оптимумом.