5.2. Метод ветвей и границ

Алгоритм метода ветвей и границ можно представить такой последовательностью шагов:

Шаг 1. Решается линейно ослабленная задача. Если получено целочисленное решение, то задача решена, иначе переход к шагу 2.

Шаг 2. Рассматриваем любую переменную (например, x_j), которая приняла нецелочисленное значение. Для нее составляет два ограничения:

а) x_j  [x_j^opt]; б) x_j  [x_j^opt] +1,

где [x_j^opt] – целая часть оптимального значения переменной x_j.

Шаг 3. На основе исходной задачи составляем две задачи: первая содержит ограничения исходной + ограничение а); вторая – ограничения исходной + ограничение б). Переход к шагу 1.

Таким образом, построение новых задач приводит к возрастанию дерева задач. Если по какой-то из ветвей получается целочисленное решение, оно берется в качестве ориентира (Z^{ориент.}). С ним впоследствии будут сравниваться вновь получаемые целочисленные решения. Процесс решения по каждой из ветвей продолжается до тех пор, пока не встретится один из следующих случаев:

1. Получено новое целочисленное решение. Если оно лучше ориентира Z^{ориент.}, оно берется в качестве нового ориентира, если хуже – отбрасывается.

2. Получено недопустимое решение.

3. Получено нецелочисленное решение, которое хуже найденного ранее ориентира Z^{ориент.}. Исходя из утверждения 1, целочисленное решение по этой ветви окажется хуже найденного ранее.

Рассмотрим применение этого метода на примере 5.2.

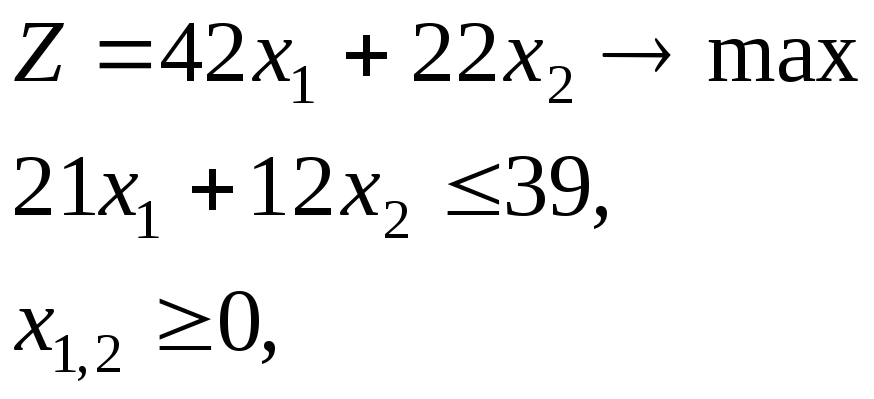
x_1,2 – целые.

Исходя из решения линейно ослабленной задачи (1 6/7; 0), сформируем две задачи:

1) исходная + ограничение x₁  2;

2) исходная + ограничение x₁  1.

Задача 1) не имеет решений, поскольку ОДЗ – пустое множество.

Решим графическим методом задачу 2) (рис. 5.2)

Р ис. 5.2. Решение задачи примера 5.2 с ограничением x₁  1.

Решением задачи 2) является (1; 1,5), которое нецелочис­лен­ное. Разобьем эту задачу на две:

21) задача 2) + ограничение x₂  2 (рис. 5.3 а);

22) задача 2) + ограничение x₂  1 (рис. 5.3 б).

а) б)

Рис. 5.3. Решение задачи примера 5.2 с ограничением x₁  1: а) с ограничением x₂  2; б) x₂  1.

Решение задачи 21): x₁ = 5/7; x₂ = 2; Z₂₁ = 74. Решение нецелочисленное.

Решение задачи 22): x₁ = 1; x₂ = 1; Z₂₂ = 64. Данное решение целочис­ленное, поэтому задачу 22) уже не разбиваем, а ее решение берем в качестве ориентира Z^{ориент.} = 64.

Поскольку Z₂₁ = 74 > Z^{ориент.}, задачу 21) разобьем на две:

211) задача 21) + ограничение x₁  1 – она не имеет решений, так как ОДЗ – пустое множество;

212) задача 21) + ограничение x₁ = 0. Получим решение (0; 3,25), Z₂₁₂ = 71,5. Решение нецелочисленное. Поскольку Z₂₁₂ > Z^{ориент.}, продолжаем разбиение:

2121) задача 212) + ограничение x₂  4 – не имеет решений, так как ОДЗ – пустое множество.

2122) задача 212) + ограничение x₂  3. Ее решение (0; 3), Z₂₁₂₂ = 66. Поскольку Z₂₁₂₂ > Z^{ориент.} = 64, это решение является окончательным.

Оптимум наблюдается в точке (0; 3).

В итоге получили следующее дерево решения задачи (рис. 5.4):

Рис. 5.4. Дерево решений целочисленной задачи примера 5.2