
- •Донецкий университет экономики и права
- •Кафедра высшей математики и информационных технологий
- •А.А. Мадых, к.Э.Н.
- •Экономико-математическое моделирование
- •Курс лекций
- •Часть 1
- •Донецк ДонУэп 2010
- •Содержание
- •Введение
- •Тема 1 концептуальные аспекты математического моделирования экономики
- •1.1. Понятие модели. Классификация моделей
- •1.2. Этапы моделирования
- •Тема 2 оптимизационные экономико-математические модели
- •2.1. Понятие оптимизационной модели
- •2.2. Примеры постановки оптимизационных задач
- •Тема 3 задачи линейного программирования и методы их решения
- •3.1. Графический метод решения задач линейного программирования
- •3.2. Симплекс-метод решения задач линейного программирования
- •3.3. Метод искусственного базиса
- •3.4. Специальные случаи решения задач линейного программирования
- •Тема 4 теория двойственности и анализ линейных моделей оптимизационных задач
- •4.1. Понятие и экономический смысл двойственной задачи
- •4.2. Двойственный симплекс-метод
- •4.3. Анализ чувствительности
- •4.3.1. Изменение коэффициента целевой функции при небазисной переменной
- •4.3.2. Изменение коэффициента целевой функции при базисной переменной.
- •4.3.3. Изменение правой части ограничения
- •4.3.4. Изменение колонки коэффициентов при небазисной переменной. Оценка эффективности новых способов производства
- •Тема 5 целочисленное программирование
- •5.1. Понятие задачи целочисленного программирования
- •5.2. Метод ветвей и границ
- •5.3. Метод отсекающих плоскостей (Гомори)
- •Тема 6 нелинейные оптимизационные модели экономических систем
- •6.1. Понятие нелинейных оптимизационных моделей и подходы к их решению
- •6.2. Метод множителей Лагранжа
- •Литература
- •Відповідальний за випуск: завідувач кафедри вищої математики та інформаційних технологій к.Ф-м.Н., доцент л.М. Харламова
- •83048, М. Донецьк, вул. Університетська, 77
4.3.4. Изменение колонки коэффициентов при небазисной переменной. Оценка эффективности новых способов производства
Изменение технологии выпуска какого-либо вида продукции может привести к изменению колонки коэффициентов в ограничениях и соответствующего коэффициента в ЦФ. Чтобы определить, как это повлияет на решение, рассматривают соответствующее ограничение двойственной задачи. Если оно оказывается непротиворечивым, следовательно, изменение технологических коэффициентов (появление возможности выпуска нового вида продукции), не влияет на текущее оптимальное решение.
Пример 4.2. Пусть в примере 3.2 изменилась технология производства столов: он продается по 43 у.е., но используется 5 м2 древесины и по 2 часа времени на столярном и отделочном участках. Выгодно ли станет их выпускать?
Рассмотрим соответствующее ограничение двойственной задачи:
![]()
Подставляя в него оптимальное решение двойственной задачи (0;10;10;0), получим: 40 43, которое противоречиво. То есть текущее решение не оптимально, и x2 нужно ввести в базис. Это и понятно, поскольку фабрика использует ресурсов на 2·10 + 2·10 = 40 у.е., а продает по 43, следовательно, выгодно ввести столы в базис, и на каждом столе иметь дополнительно 3 у.е. дохода. Если бы цена такого стола была 40 грн. и меньше, текущее решение не изменилось бы.
Пример 4.3. Пусть фабрика в примере 3.2. может выпускать еще и скамеечки по цене 15 у.е., затрачивая 1,5 м2 древесины и по 1 часу на столярном и отделочном участках. Выгодно ли запускать скамеечки в производство?
Соответствующее двойственное ограничение имеет бы вид:
1,5![]()
Подставляя в него оптимальное решение двойственной задачи (0;10;10;0), получим: 20 15. Удовлетворение этого ограничения говорит о том, что текущее базисное решение не изменится. Тратить ресурсов на 20 у.е. и продавать по 15 у.е. не выгодно и скамеечки производить не стоит. Минимальная цена, по которой такие скамеечки имеет смысл продавать – 20 у.е.
Тема 5 целочисленное программирование
5.1. Понятие задачи целочисленного программирования
Начнем рассмотрение задач целочисленного программирования с примера.
Пример 5.1. Компания может инвестировать средства по четырем направлениям: инвестиции №1 принесут доход в 16 тыс. грн., инвестиции №2 – в 22 тыс., №3 – 12 тыс., №4 – 8 тыс.
Каждая из инвестиций требует вложения денег в настоящее время: для инвестиции №1 – 5 тыс., №2 – 7 тыс., №3 – 4 тыс., №4 – 3 тыс.
В распоряжении компании имеется 14 тыс. грн. Сформулировать задачу целочисленного программирования, которая бы позволила максимизировать доход компании, полученный от инвестиций.
Определим переменные. Пусть

Тогда доход компании будет описываться выражением
![]() ,
,
которое нужно максимизировать. Поскольку затраты на инвестиции должны быть не больше 14 тыс., имеем модель целочисленного программирования с одним ограничением:
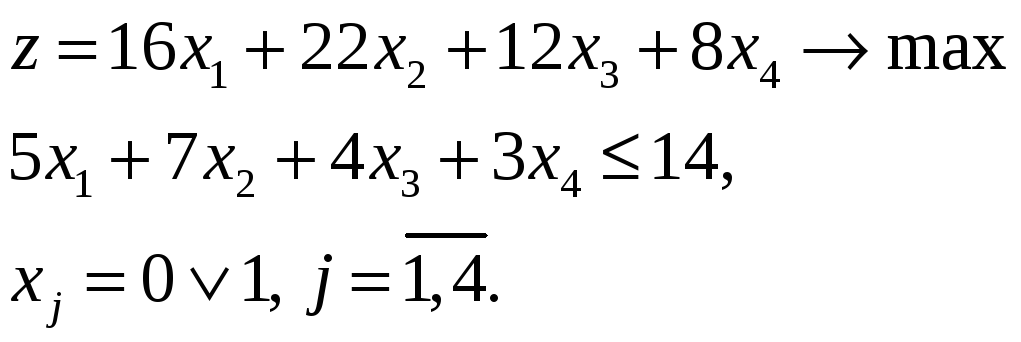
Данную задачу целочисленного программирования с булевыми переменными совершенно не имеет смысла решать симплекс методом: решение z = 44,8 при x1 = 2,8, x2 = x3 = x4 = 0 нас устроить не может, поскольку по смыслу нельзя 2,8 раз осуществить одну и ту же инвестицию.
Можно выйти из
положения так: дополнить эту задачу
ограничением xj 1, ![]() ,
тогда решение, полученное симплекс-методом,
будет z
= 44 при x1 = x2 = 1,
x3
= 0,5, x4 = 0.
Это решение тоже нас не может удовлетворить,
поскольку инвестицию №3 нельзя осуществить
наполовину. Если же округлить x3
до 1, получим недопустимое решение (нужно
потратить 16 тыс.), округление же x3
до 0 даст решение, далекое от оптимального
(z
= 38).
,
тогда решение, полученное симплекс-методом,
будет z
= 44 при x1 = x2 = 1,
x3
= 0,5, x4 = 0.
Это решение тоже нас не может удовлетворить,
поскольку инвестицию №3 нельзя осуществить
наполовину. Если же округлить x3
до 1, получим недопустимое решение (нужно
потратить 16 тыс.), округление же x3
до 0 даст решение, далекое от оптимального
(z
= 38).
Оптимальным же решением будет x1 = 0, x2 = x3 = x4 = 1, которое дает z = 42 тыс.
Сформулируем несколько важных положений.
Задача линейного программирования, у которой все переменные могут принимать только целые значения, называется полностью целочисленной задачей.
Задача, у которой некоторые переменные могут принимать только целые значения, называется частично-целочисленной задачей.
Задача, у которой некоторые переменные могут принимать значения только 0 или 1, называется задачей с булевыми переменными.
Задача целочисленного программирования, которая получается путем отмены ограничений на целочисленность или ограничений типа «0 или 1», называется линейно-ослабленной задачей.
Утверждение
1. Решение
задачи целочисленного программирования
всегда не лучше, чем решение
линейно-ослабленной задачи. Для задачи
на максимум
![]() ,
а для задачи на минимум:
,
а для задачи на минимум:
![]() .
.
Утверждение 2. Если ОДЗ линейно-ослабленной задачи является ограниченным множеством, то ОДЗ целочисленной задачи содержит конечное число точек.
Отсюда следует 3 подхода к решению целочисленных задач:
-
Путем прямого перебора и сравнения всех точек. Очевидно, что применение этого метода весьма ограничено. Во-первых, если ОДЗ линейно-ослабленной задачи является неограниченным множеством, то количество точек целочисленной задачи будет бесконечным, во-вторых, даже при конечном числе точек прямой перебор может оказаться очень длительной и неэффективной процедурой.
-
Путем округления решения линейно-ослабленной задачи до целых. Из примера 5.1 видно, что этот метод тоже далеко не всегда применим, а решение задачи, полученное путем округления, может оказаться далеким от оптимального. Применяется этот метод, если переменные принимают достаточно большие значения, например, если получилось, что нужно выпускать 1003,4 единиц продукции, то округление до 1003 может быть вполне приемлемым.
-
Путем построения дополнительных ограничений в рамках имеющегося ОДЗ с целью отсечения нецелочисленных значений переменных. На этом подходе основано два метода решения задач целочисленного программирования, которые будут рассмотрены в п.п. 5.2 и 5.3: метод ветвей и границ и метод отсекающих плоскостей.
Пример 5.2. Рассмотрим задачу:
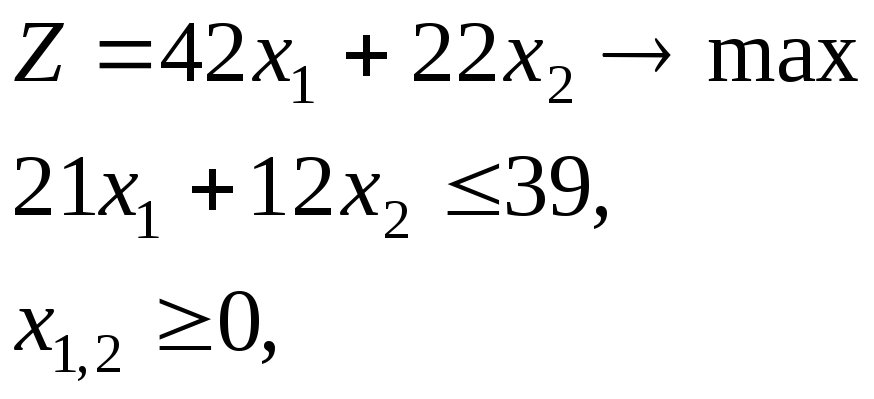
x1,2 – целые.
ОДЗ представляет собой 6 точек: (0;0), (0;1), (0;2), (0;3), (1;0), (1;1). Методом перебора легко получить, что оптимальное решение (0;3) и Z = 66 (рис. 5.1).
Р ис.
5.1. Решение графическим способом задачи
примера 5.2
ис.
5.1. Решение графическим способом задачи
примера 5.2
Оптимальное же решение линейно-ослабленной задачи будет (1 6/7; 0) и Z = 78.
Очевидно, что округление решения линейно-ослабленной задачи в меньшую сторону (1; 0) с Z = 42 – далеко от оптимального, округление же в большую сторону (2; 0), вообще является недопустимой точкой.
Пример 5.3.
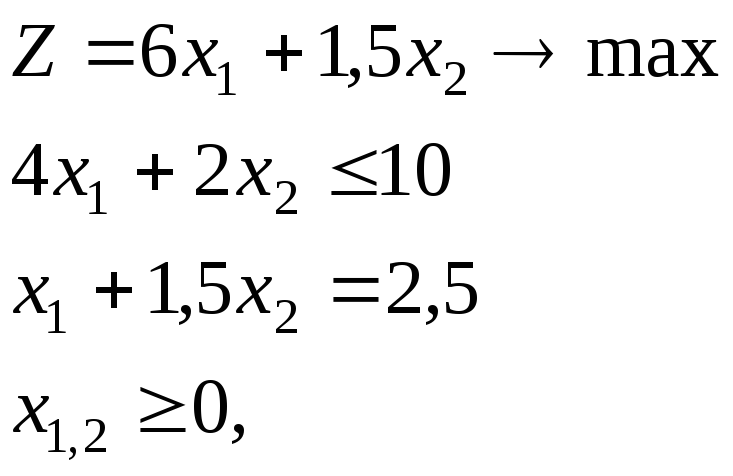
x1,2 – целые.
Оптимальное решение линейно-ослабленной задачи (2,5; 0), Z = 15. Однако округления (2; 0) и (3; 0) являются недопустимыми точками. Оптимальным же решением данной задачи является точка (1; 1), Z = 7,5.
