4. Алгоритмы идентификации и прогнозирования состояния системы

Идентификация состояния системы в текущей ситуации сводится к диагностированию причин ее возникновения, прогнозированию дальнейшего состояния, анализу и оценке возможностей достижения цели.

Ситуационная матрица позволяет определить формальную процедуру идентификации аномальной ситуации, представленной в качестве примера на рис.1.7 в аналоговой форме в виде распределения точек, площадь которых пропорциональна значению соответствующих элементов матрицы.

Исходя от максимального диагонального элемента, соответствующего максимальному отклонению от нормы - х₁₃ в наблюдаемом множестве параметров состояния системы, следует перемещение по строке (рис.1.7) с выявлением причин, вызвавших отклонение данного параметра, и выбором наиболее значимой. Далее следует переход по столбцу к новому элементу главной диагонали, после чего вновь оцениваются элементы соответствующей строки. Поиск продолжается до нахождения отклонения, в строке которого все недиагональные элементы будут равны нулю, например . Это означает, что данное отклонение является одной из основных исходных причин возникновения аномальной ситуации.

Р ис. 1.7. Структурно-параметрическая ситуационная модель аномального

состояния системы в пространстве контролируемых параметров х₁,…, х₃₂

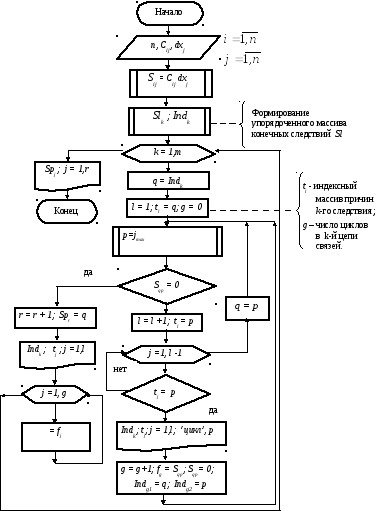
Алгоритм идентификации содержит (рис.1.8) блок формирования ситуационной матрицы и процедуру поиска причин аномального состояния системы. Процедура представляет собой цикл перебора независимых отклонений, внутри которого происходит отыскание максимального элемента в строке, запоминание его порядкового номера p и перехода на p-ю строку с повторением поиска максимального элемента этой строки.

Для обнаружения возможного зацикливания причинно-следственных связей формируется массив t_l индексов диагональных элементов, входящих в

траекторию взаимодействия, и при совпадении двух элементов этого массива следует сигнал “цикл”. При этом причина может оказаться внутри или вне контура цикла. Для выхода из причинно-следственного цикла и продолжения поиска исходной причины разрывается последнее звено обратной связи, т. е. элемент s_qp = 0, с запоминанием его значения f_g = S_qp и адресов в индексных массивах Ind_g1 ; Ind_g2 . Тогда при повторном переборе элементов q-й строки процедура либо остановится на последнем звене цикла (если причина лежит в контуре цикла), либо пойдет дальше по ступеням взаимосвязей до следующей промежуточной или конечной причины или нового цикла (рис.1.8). При переходе к выявлению причинно-следственной цепи следующего k+1 - го следствия прерванная связь j-го цикла предшествующей траектории связей восстанавливается, т.е. = f_j.

Для нахождения воздействия других факторов на очередное k-е