3. Структурно  параметрическая модель динамики состояния большой технологической системы

Технологическая система перерабатывающего предприятия АПК представляет собой множество функционально связанных процессов и аппаратов, объединенных сетью материальных, энергетических и информационных потоков. Целевая функция системы заключается в обеспечении полноты и глубины переработки исходного сырья с максимизацией выхода и качества готовой продукции при минимуме ресурсного обеспечения и затрат.

Технологическая система может быть представлена в виде направленного графа, узлы которого соответствуют технологическим операциям, а ветви – материальным потокам сырья, промежуточным и конечным продуктам так, что выходной поток одного узла является входом другого смежного узла. Каждая ветвь описывается набором физико-химических показателей и параметров состояния потока, а каждый узел  математической моделью, связывающей характеристики его входов и выходов.

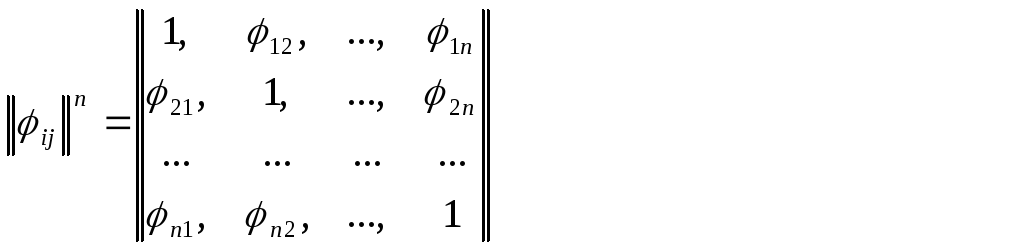
На основе технологического графа с параметрическими и функциональными описаниями можно составить матричную модель технологической системы, упорядочивающей в форме квадратной матрицы все множество известных параметров состояния X и связей между ними _ij,

x₁, x₂, … , x_n

(1-6)

где _ij – нормированные коэффициенты или функции связи между i-м и j-м элементами в системе уравнений

(1-7)

В общем случае _ij отражает интенсивность влияния j-го параметра на

i-й и каждая строка матрицы описывает вектор связей, влияющих на i-й показатель состояния системы. В свою очередь, каждый j-й столбец матрицы описывает вектор влияний j-го фактора на другие параметры состояния системы. При отсутствии влияния характеристика связи становится равной нулю, т.е. _ij = 0.

Таким образом, матрица является оператором взаимодействия элементов технологической системы.

Отыскание коэффициентов связей _ij производится из аналитических описаний x_i =  (x₁, x₂, …, x_n) ; , экспертных оценок или из уравнений множественной регрессии

; (1-8)

на основе обработки статистических данных или планирования эксперимента.

В зависимости от степени детализации такая модель может описывать как отдельные процессы и технологические линии, так и весь технологический комплекс с выделенными подсистемами и функциями цели. В общем случае, выделив группу выходных параметров системы (например, показателей качества готовой продукции, параметры состояния технологических процессов, характеристики входных потоков и другие группы), можно сформировать структурно-параметрическую модель большой технологической системы.

x₁, x₂,…,x_k , x_k+1, … , x_m , x_m+1,…, x_n

1

1

...

1

1

1

1

...

...

...

1

1

1

...

1

Операторы функциональных связей внутри выделенных групп параметров упорядочиваются вдоль главной диагонали клеточной матрицы и при независимости факторов становятся единичными диагональными матрицами и т.д. В случае взаимосвязанности элементов в диагональной клетке помещается матрица оператора взаимодействия .

Недиагональные клетки соответствуют операторам прямого и косвенного влияния различных функциональных групп друг на друга и на качественные показатели целевой функции или функционала.

Таким образом, клеточная матрица представляет полное описание структуры и значимости связей между параметрами и факторами, определяющими функционирование технологического процесса или комплекса в целом. Определяющие факторы в общем случае могут быть обобщенными (в зависимости от степени детализации) и тогда коэффициенты их влияния, в свою очередь, представляются операторами. Степень детализации формальных описаний объекта в виде клеточной матрицы определяется конкретной задачей функционального анализа и моделирования, а также характером и полнотой априорных данных о качественных и количественных показателях влияния и взаимодействия.

При имеющихся статистических данных о состоянии системы и среды в виде массива x_kj ; , где x_kj – значение j-го фактора в k-м опыте, составляется матрица коэффициентов корреляции

, (1-9)

где - средние значения i-го и j-го факторов;

- среднеквадратичные отклонения соответствующих факторов.

Характер связей между коррелируемыми факторами определяется коэффициентами линейной множественной регрессии

(1-10)

с коэффициентами связи P_ij j-го фактора c i-м.

Для сопоставимой оценки отклонений и связей параметров различной физической природы и размерности формируется матрица безразмерных характеристик

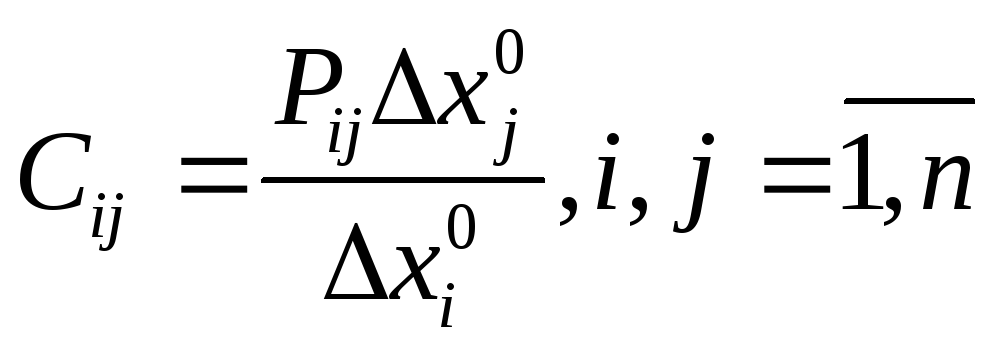, (1-11)

где x_i⁰ и x_j⁰ - допустимые отклонения от нормы.

По найденной матрице характеристик взаимосвязей C_ij; и вектору текущих отклонений x₁, …, x_{n ,} путем умножения C_ij ⁿ на диагональную матрицу нормированных отклонений х_j_jk, формируется ситуационная матрица состояния системы.

(1-12)

где 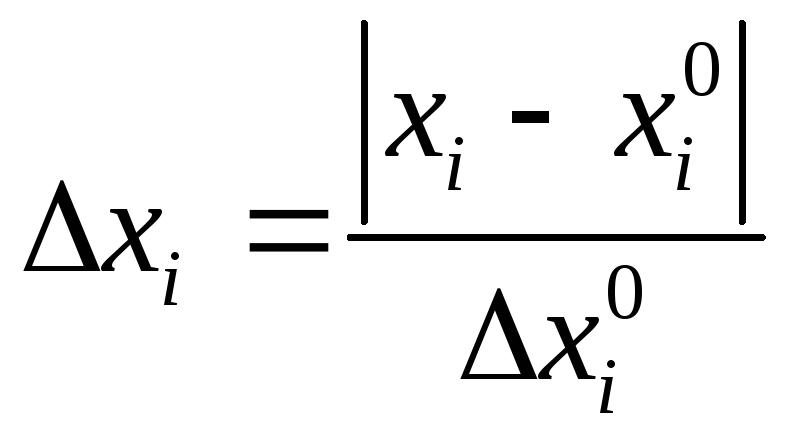; - нормированные отклонения параметров состояния

от диапазона допустимых отклонений .

Элементы главной диагонали ситуационной матрицы ; отображают текущие нормированные отклонения х_i контролируемых факторов от заданных значений, а недиагональные – вклады других отклонений х_j , в отклонение х_{i ,} с размещением по строкам всех априорно известных причин отклонения х_i , а по столбцам – возможных следственных влияний отклонения х_i на другие параметры.

В общем случае ситуационная матрица является структурно-параметрической моделью изменения состояния большой системы с множеством функциональных узлов и связей между ними и описывает структурно-сложную ситуацию причинно-следственного взаимодействия элементов в текущем состоянии системы объединяя априорные данные о структуре связей с текущей информацией х.