1.2.1. Анализ элементов

Исследование структуры системы в первую очередь направлено на выявление:

- изолированных вершин, не инцидентных ни одному из ребер графа (т.е. не имеющих ветвей связей);

- висящих или входных, в которые нельзя попасть ни из какой-либо другой вершины графа;

- тупиковых или выходных вершин, из которых нельзя попасть в другие вершины графа.

Матрица смежности в соответствии со структурой системы отражает по строкам все исходящие из i-й вершины связи, а по столбцам – все связи, входящие в нее. Поэтому при анализе элементов признаком изолированной вершины являются нулевые недиагональные элементы ее строки и столбца, а признаками входных и выходных вершин – нулевые недиагональные элементы, соответственно, их столбцов и строк.

В случае если сумма элементов строки больше суммы элементов соответствующего столбца:

то имеет место узел разветвления связей в структуре системы. В обратном случае - свертка.

Все элементы могут быть оценены и упорядочены по их рангу, определяющему количество связей данного элемента со всеми остальными элементами:

; . (1-1)

Чем выше ранг элемента, тем более тесно он связан с другими элементами и тем больше последствий вызывает изменение его состояния и поведения.

1.2.2. Анализ связей

Анализ связей на графе заключается в нахождении и оценке путей между любыми его двумя вершинами i и j, количества путей, числа ступеней связи, кратчайших путей; а также петель, контуров-циклов, сильно-связанных подграфов и разделяющих связей.

Петли – означают наличие связи между входом и выходом одного и того же элемента.

Контур-цикл образует путь как чередующуюся последовательность ребер и вершин, в которой начальная и конечная вершины совпадают.

Подграф называется сильно-связанным, если все входящие в него вершины взаимно достижимы, т.е. образуют сеть.

Наличие прямых циклических контуров связей характеризуется равенством S_ij = S_ji = 1.

Важнейшей задачей анализа связей является нахождение связи между элементами при априорной неопределенности ее существования в заданной структуре системы с равнозначными связями. Сложность решения задачи возрастает с увеличением числа вершин-разветвлений на пути от исходного элемента к конечному и увеличением выбора.

Моделью алгоритма нахождения связи между элементами системы может служить поиск пути в конечном лабиринте [7] с клубком нити “Нить Ариадны”, один конец которой закреплен на исходной площадке. По мере углубления в лабиринт сложной системы нить разматывается и при достижении цели будет протянута через последовательность коридоров (ветвей), соединяющих исходный элемент с конечным. Если цель недостижима, нить вновь сматывается в клубок и поиск прекращается у исходного пункта. Логический алгоритм поиска (рис.1.2) основан на просмотре строки матрицы смежности ; до нахождения в ней.

первого единичного элемента с формированием индексного массива элементов, через которые проходит путь между t-й и p-й вершинами по рекурсивной схеме:

q = t; l =1; Ind_l = q;

l = l +1; Ind_l = r; q = r,

где q, r – индексы последовательно смежных вершин в линии связи.

Начиная с t-й строки q = t; l = 1; , в цикле перебора элементов q-й строки отыскивается первая возможная ветвь связи ; с некоторым j-м элементом. После запоминания его r = j и занесения в индексный массив l=l+1; производится (рис.1.2) проверка достижения цели r = p и возможного зацикливания процедуры поиска, т.е. возврата к ранее пройденным вершинам, сравнением r с предыдущими элементами индексного массива ; . Если r = p, то p-я вершина достигнута и следует остановка, если же цель не достигнута и цикл не образуется, следует повторение просмотра текущей q-й строки для q = r.

В случае образования цикла, когда r оказывается равным ранее зарегистрированному индексу в массиве , последнее звено связи разрывается, т.е. ; делается шаг назад l = l -1 (сматывание нити) и цикл “просмотра” q-й строки повторяется.

При достижении тупикового элемента с нулевой строкой следует также шаг назад и разрыв тупиковой связи ; l=l-1. Если при этом оказалось, что l -1=0, то цель - p-я вершина - не достижима из t-й вершины.

Рассмотренный алгоритм может быть использован в решении многих практических задач анализа сложных систем и выбора пути на очередном шаге следования от входа в систему (исходного состояния) к ее выходу (конечной цели).

Один из способов описания и оценки путей связан с алгебраическими свойствами матрицы.

1. Главный определитель матрицы S_ij характеризует число замкнутых циклов взаимодействия так, что каждое его слагаемое за исключением диагональных соответствует одному их циклов.

2. Слагаемые диагонального минора M_ij ^n-1 матрицы S_ij характеризуют число и характер замкнутых циклов, остающихся в структуре после исключения i-го элемента.

3. Слагаемые недиагонального минора M_lk^n-1 матрицы смежности S_ij при исключении l-й строки и k-го столбца описывают число и характер связей k-го элемента с l-м в направлении от S_k к S_{l ,} т.е. .

Например:

1 a₁₂ a₁₃

1

det a₂₁ 1 a₂₃ =

a₃₁ a₃₂ 1

Исходя из свойств матрицы смежности, можно построить полную матрицу путей,где p_ij - число путей из i-й вершины к j-й; либо отыскать отдельные ее элементы для заданных входных и выходных вершин. Практически важным вопросом исследования структуры связей является определение кратчайшего пути из одной вершины в другую. Однако при большой размерности графа определение его “вручную “ практически невозможно и связано с использованием специальных алгоритмов поиска кратчайших расстояний.

Исходя из матрицы смежности S_i,j, алгоритм нахождения количества путей и кратчайшего пути между i-м и j-м элементами связан с построением матрицы смежных расстояний Sr_i,j; ; с элементами

1 при S_{i,j =} 1

1E6 при S_i,j =0

0 при i = j

Sr_i,j =

и нахождением на ее основе строковой матрицы описаний кратчайших путей W_i,j, дистанционной матрицы d_ij минимального числа ступеней связи между i-м и j-м элементами и матрицы количества путей p_i,j с элементами, равными при i  j числу путей от i-й вершины к j-й, а при i = j - числу циклов, проходящих через i-й элемент, включая собственный.

А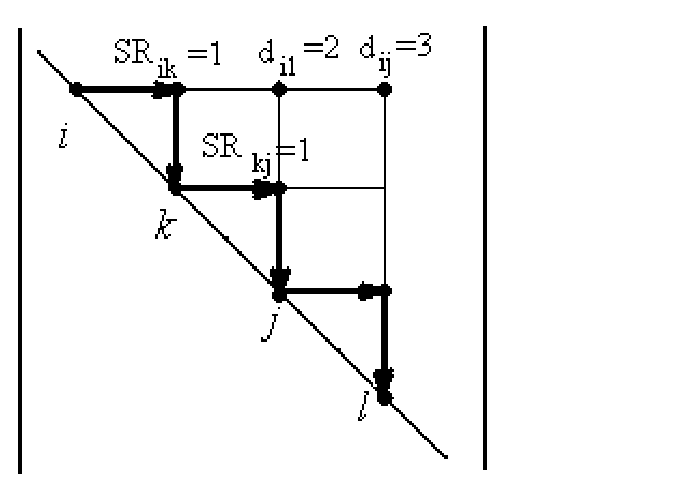 лгоритм поиска кратчайшего пути, приведенный на рис.1.3, основан [4] на выборе текущего k-ого элемента и проверке возможности прохождения через него контура связи между любым i-м и j-м элементами (алгоритм Флойда) по следующей схеме

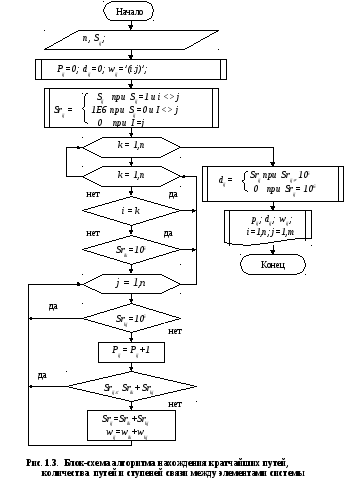
При этом в каждом цикле по при наличии связи i  k  j предшествующее значение Sr_i,j заменяется на более короткую дистанцию, проходящую через k-ю ступень, с записью составляющих пути в строковый массив w_i,j .