Задача 3.4. Приближённое определение частоты собственных колебаний

b_m / 2

Требуется определить частоту основного тона собствен-ных колебаний сооружения башенного типа с расчётной схемой по рис. 3.44 в виде консольного стержня

к

m₍₁₎

усочно-постоянного сечения с сосредото-

ч

y₁

енными массами, задавшись приближён-

ным описанием его оси при изгибе в про-

цессе колеб

y₂

EI

аний.

m₍₂₎

y₄

y₃

y(x)

2EI

4EI

Верхняя масса m₍₁₎ = 2m – треугольно-

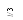
го очертания, постоянной толщины; две

другие – точечные: m₍₂₎ = m ; m₍₃₎ = 3m .

m₍₃₎

Р е ш е н и е

Учитывая преобладающий вид дефор-

мации консоли ( изгиб ) и инерцию враще-

ния верхней массы, определяем число сте-

пеней свободы масс как n = 4 ( на рис. 3.44

обозначены y₁ , …, y₄ ) . Рис. 3.44

Главную форму колебаний с минимальной собственной час-тотой качественно можно предсказать: она характеризуется од-нозначными отклонениями масс, как показано на рис. 3.44. При точном решении ось изогнутого стержня на каждом участке постоянного сечения представляет собой параболу 3-й степени, что следует из дифференциального уравнения изгиба прямоли-нейного стержня d ⁴ y (x) / dx ⁴ = q (x) / [EI (x)] = 0 ( q (x) = 0, так как распределённые д’аламберовы силы инерции отсутствуют). Поэ-тому для приближённого решения задачи вместо трёх истинных участков разных кубических парабол принимаем единую кри-вую, задаваемую полиномом 3-й степени

y (x) = 0,5 y₁(x/l)² (3 – x/l),

удовлетворяющим кинематическим условиям = 0, = 0, = y₁ . Вследствие этого перемещения y₂ , y₃ и y₄ выражаются через y₁: y₂ == 3 y₁/(2l) ; y₃ == (14/27) y₁ ; y₄ ==

= (4/27) y₁ , что означает переход к обобщённому ( групповому ) перемещению с параметром = y₁ и компонентами, описываемы-ми через посредством коэффициентов 3/(2l) , 14/27 и 4/27, ко-торые найдены из принятой аппроксимации y(x).

Связь между исходными перемещениями y = [ y₁ y₂ y₃ y₄ ]^т и

параметром обобщённого перемещения = y₁ :

y = _, где _= [ 1 3/(2l) 14/27 4/27 ]^т .

Используем матрицу преобразования_ для определения приведённой массы, соответствующей групповому перемеще-нию : , здесь – исходная матрица масс ( с учётом инерции вращения неточечной массы 2m ):

I _m0(1) = .

, где e_m = 2h_m / 3 ; I_m(1) = I_m0(1) + m₍₁₎;

Получаем

₁₁

При b_m = 0,2 l и h_m = 0,1 l имеем 2,7647 m . Далее расчёт выполняем по схеме системы с одной степенью свободы массы ( рис. 3.45, а ) по частотному уравнению

r

EI

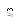
₁₁ – = 0 или ₁₁ – = 0,

где r₁₁ = 1/₁₁ . Вычислив коэф-

ф

2EI

ициент податливости ₁₁ как а) б)

перемещение от единичной си-

л

4EI

ы инерции приведённой массы

( рис. 3.45, б ) методом Максвел-

л

Рис. 3.45

а – Мора, получаем

₁₁ = и .

Без учёта инерции вращения массы m₍₁₎ приведённая масса будет 2,3347 m, тогда – отличается от най-денного выше значения на 8,8 % , причём в сторону завышения,

что всегда опасно, так как может приводить к неправильным ( бо-лее оптимистичным, чем действительные ) оценкам динамичес-ких эффектов при вибрационных и иных периодических воз-действиях в дорезонансном режиме.

Решение для системы с четырьмя степенями свободы масс

( точное для схемы по рис. 3.45 ) даёт ; следо-

вательно, приближённый результат получен с погрешностью 0,45 % и может оцениваться как вполне приемлемый с практи-ческой точки зрения.

Дополнительно рассмотрим другой ( более простой ) вариант аппрокси-мации уравнения оси изогнутого стержня: y (x) = ( x / l ) ² y₁. В этом случае матрица преобразования будет  _y = [ 1 2/l 4/9 1/9 ]^т, приведённая масса

искомая частота – отклонение от точного значения состав-ляет 0,57 %, что лишь немногим больше, чем в первом варианте.

Заметив, что вычисленные значения частоты  в двух вари-антах имеют разнозначные погрешности ( правда, обнаружить это можно только из сопоставления с точным результатом, неиз-вестным в приближённом расчёте ), можно либо принять в каче-стве уточнённой величины полусумму найденных частот ( полу-чается – практически точное значение), либо использовать описание оси консоли при колебаниях в виде полу-суммы выражений по двум вариантам:

y (x) = [ 0,5 (x/l)² (3 – x/l) + (x/l)² ] y₁ = 0,25 (x/l)² (5 – x/l) y₁,

тогда _y = [ 1 7/(4l) 13/27 7/54 ]^т ; приведённая масса

= 2,7897 m; частота – совпадение с точным результатом во всех учитываемых значащих цифрах.

1

1

₂₂

Используем ещё один приближённый способ определения минимальной частоты собственных колебаний – по формуле Донкерлея ( 1.143 ):

1

₁₁₍₁₎

₁₁₍₂₎

₃₃

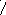
г

1

де – частоты, опреде-

ляемые по схемам рис. 3.46.

Применение этого способа

к рассматриваемой системе имеет Рис. 3.46

особенность, обусловленную тем, что одна из масс – неточечная, с двумя степенями свободы. Учитываем их одновременно, вычис-

л

яя как меньший из корней частотного уравнения

где

Уравнение частот получается в виде

( здесь ₁ = EI / ( ml ³² ) )

или – 0,291728₁ + 2,0633= 0, откуда _{1, max} = 0,29243

(_{1, min} ) ^–2 =() ^–2 = 0,29243 ml ³ / EI.

Остальные слагаемые формулы Донкерлея:

= m₍₂₎₂₂ ; = m₍₃₎₃₃ ,

где m₍₂₎ = m ; m₍₃₎ = 3m ; ₂₂ = (3/108) l³ / EI ; ₃₃ = (1/324) l³ / EI .

Суммируя , и , находим

0,32947 ml ³/EI и – погрешность это-

го приближённого результата – 1,7 %.

Без учёта инерции вращения верхней массы получается () ^–2 = m₍₁₎ ₁₁₍₁₎ = 0,22840 ml ³ / EI, тогда .