
- •Двунаправленная ассоциативная память.
- •Основные понятия генетических алгоритмов.
- •Классический генетический алгоритм.
- •Решение комбинаторных задач с помощью генетических алгоритмов.
- •Пример 5
- •Интеллектуальные информационные системы в условиях неопределенности и риска.
- •Основные понятия теории нечетких множеств.
- •Лингвистические переменные и нечеткие правила вывода.
- •Системы нечеткого вывода Мамдани-Заде.
- •Фазификатор и дефазификатор
- •Модель Мамдани-Заде как универсальный аппроксиматор.
Двунаправленная ассоциативная память.
Обобщением сети Хопфилда на случай двухслойной рекуррентной структуры позволяющей кодировать множество двух взаимосвязанных векторов считается двунаправленное ассоциативное запоминающее устройство, называемое ДАП. В этой сети сигналы распространяются в двух направлениях: если в первом цикле сигналы в начале проходят в одну сторону для задания состояния нейронов-получателей, то в следующем цикле эти нейроны сам становятся источниками, высылающими сигналы в обратную сторону.
Этот процесс повторяется до достижения состояния расвновесия
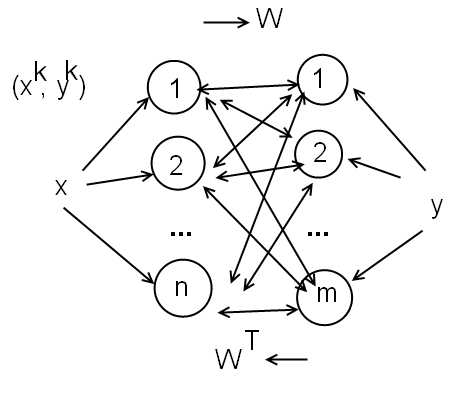
Функция активации
нейронов имеет пороговый характер. На
этапе обучения используются биполярные
сигналы (1 и -1). Матрица весов W
связывающая оба слоя сети является
действительной и в общем случае
несимметричной. Пр прямом распространении
сигналов они умножаются на весовые
коэффициенты матрицы W,
а при обратном – на весовые коэффициенты
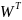 .
.
Предположим, что
обучающие данные представляют собой
множество пар
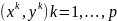 эталонных биполярных векторов. На основе
этого множества формируется матрица
эталонных биполярных векторов. На основе
этого множества формируется матрица
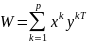 .
В результате процесса двунаправленной
обработки сигналов формируется 2
устойчивых вектора
.
В результате процесса двунаправленной
обработки сигналов формируется 2
устойчивых вектора
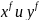 ,
которые удовлетворяют следующим
уравнениям:
,
которые удовлетворяют следующим
уравнениям:
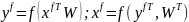 .
Каждой промежуточной точке
.
Каждой промежуточной точке
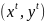 ставится в соответсвие значение
энергетической функции
ставится в соответсвие значение
энергетической функции
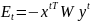 ,
которая убывает при каждом изменении
состояния
вплоть до достижения локального минимума
,
которая убывает при каждом изменении
состояния
вплоть до достижения локального минимума
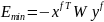 .
Где
.
Где
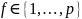 .
Сеть скатывается к одной из эталонных
пар.
.
Сеть скатывается к одной из эталонных
пар.
В режиме распознавания
при начальных значениях векторов,
совпадающих с использованными при
обучении, сеть распознает их безошибочно.
При искажении векторов x
и y,
сеть не всегда способна откорректировать
эти векторы и распознает их с определенными
погрешностями. Если размерности векторов
x
и y
обозначить через n
и m,
то удовлетворительное качество
распознавания можно получить при
выполнении следующего неравенства
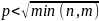 ,
где
,
где
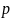 - число запоминаемых в сети пар векторов.
- число запоминаемых в сети пар векторов.
Основные понятия генетических алгоритмов.
При описании генетических алгоритмов используются определения, заимствованные из генетики.
Популяция – это конечное множество особей. Входящие в популяцию особи в генетических алгоритмах представлены хромосомами с закодированными в них множествами параметров задачи. Хромосома – это упорядоченная последовательность генов. Ген – это атомарный элемент хромосомы или генотипа. Генотип – это набор хромосом данной особи. Фенотип – набор значений соответствующих данному генотипу, составленный из параметров задачи. Аллель – значение конкретного гена. Локус – место размещения генов.
Очень важным понятием в генетических алгоритмах считается функция приспособленности. Она представляет меру приспособленности данной особи в популяции. Эта функция позволяет выбрать наиболее приспособленные особи в соответствии с эволюционных принципом выживания «сильнейших», т. е. наиболее приспособившихся.
В задачах оптимизации функция приспособленности максимизируется и называется целевой функцией. Очередная популяция в генетическом алгоритме называется поколением, т. е. вновь создаваемая популяция особей называется новым поколение или поколением потомков.
Рассмотрим пример:
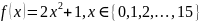
Задача оптимизации
этой функции заключается в перемещении
по пространству … для обнаружения той
точки, в которой функция принимает
максимальное значение. В качестве
параметра задачи выступает переменная
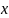 .
Множество точек
.
Множество точек
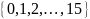 образует пространство поиска и
одновременно множество потенциальных
решений задач. Значения параметра
образует пространство поиска и
одновременно множество потенциальных
решений задач. Значения параметра
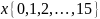 можно закодировать двоичными числами,
каждое из которых содержит 4 бита.
Представленные двоичные кодовые
последовательности называются
хромосомами.
можно закодировать двоичными числами,
каждое из которых содержит 4 бита.
Представленные двоичные кодовые
последовательности называются
хромосомами.
Фенотип |
Генотип |
0 |
0000 |
1 |
0001 |
2 |
0010 |
3 |
… |
4 |
… |
… |
… |
15 |
1111 |
Каждая из хромосом
состоит из 4-х генов. Популяция состоит
из особей, которые выбираются среди
этих 16-и хромосом. Например, популяция
с численностью хромосом = 6 может иметь
вид: {0010,0101,0111,1001,1100,1110} – популяция.
Функция приспособленности в данном
примере выражается
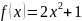 .
Приспособленность отдельных хромосом
популяции определяется значением этой
функции дя значений
,
соответствующим этим хромосомам.
.
Приспособленность отдельных хромосом
популяции определяется значением этой
функции дя значений
,
соответствующим этим хромосомам.
Пример 2.
Рассмотрим нейронную сеть:
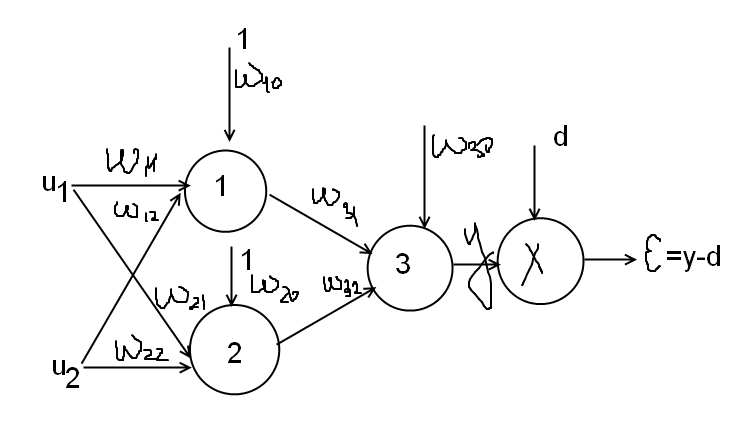
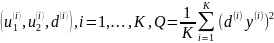
Обучение нейронной
сети заключается в настройке ее весовых
коэффициентов
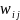 ,
с целью минимизации погрешности
,
с целью минимизации погрешности
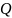 .
Допустим, что весовые коэффициенты
принимают значения из интервала
.
Допустим, что весовые коэффициенты
принимают значения из интервала
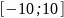 .
Тогда каждая хромосома образуется путем
конкатенации двоичных кодов, кодирующих
конкретные весовые коэффициенты.
.
Тогда каждая хромосома образуется путем
конкатенации двоичных кодов, кодирующих
конкретные весовые коэффициенты.
