
Определители
Вычислить определители:
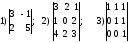 .
.Вычислить определитель
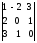
непосредственно, 2) предварительно меняя первую и третью строки,
3) предварительно меняя вторую и третью строки.
Какое предложение можно сформулировать
относительно полученных результатов? 
Вычислить определитель

1) предварительно заменив первый столбец
вектором- столбцом
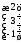 ;
;
2) предварительно заменив второй столбец
вектором - столбцом
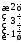 ;
;
3) предварительно заменив третий столбец
вектором- столбцом
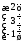 ;
;
4. Проверьте, как изменится
определитель
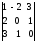 если:
если:
ко второй строке прибавить третью строку умноженную на (-2);
к первой строке прибавить вторую строку умноженную на 3;
Какое предложение можно сформулировать относительно полученных результатов?
Вычислить определители
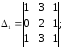

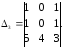
Какое предложение можно сформулировать относительно полученных результатов?
Матрицы.
Укажите размерность матриц и определите, чему равны элементы
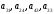

Определить параметры
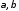 из
условий
из
условий

8. Можно ли вычислить линейную комбинацию
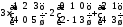 .
Ответ поясните.
.
Ответ поясните.
9. Вычислить линейную комбинацию матриц
1)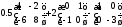 ;
2)
;
2)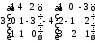 .
.
3)
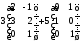 ;
4)
;
4)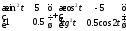 .
.
10. Вычислить линейную комбинацию
матриц
 ,
где Е- единичная матрица
,
где Е- единичная матрица
размером
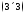 и
и
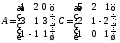
11. Решить уравнение
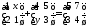
12. Вычислить произведение матриц
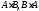

Если это невозможно, то объясните почему.
13. Вычислить произведения матриц

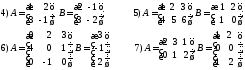
14.
Вычислить:
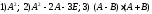 ,
где
,
где
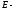 единичная
матрица;
единичная
матрица;
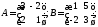
15. Найти миноры всех элементов
матрицы
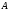
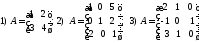
16. Вычислить данные определители
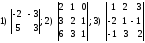
Найти матрицу
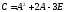 ,
если 1)
,
если 1)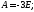 2)
2)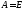 ,
где
,
где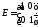 .
.Используя решение квадратного уравнения
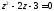 ,
найдите матрицу
,
найдите матрицу второго
порядка, которая является решением
матричного уравнения
второго
порядка, которая является решением
матричного уравнения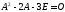 .
.Найти матрицу
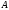 из
уравнения
из
уравнения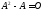 ,
где
,
где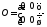 нулевая
матрица.
нулевая
матрица.Проверьте, являются ли матрицы
 взаимно обратными?
взаимно обратными?Какая из двух матриц имеет обратную
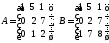 .
.
Ответ пояснить.
Вычислить матрицу
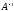 обратную
к данной матрице
обратную
к данной матрице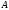
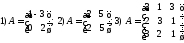 .
.
и сделать проверку полученного результата.
23. Используя элементарные преобразования , привести матрицу А к ступенчатому виду
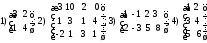 ;
;
24. Перемножить матрицы

25. Решить матричное уравнение ,
где
,
где
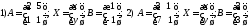
Указание. Используйте обратную
матрицу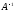 .
.
Системы линейных алгебраических уравнений
26. Проверить являются ли числа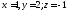 решением данной системы
решением данной системы
линейных уравнений
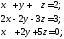
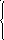
27. Проверить является ли
множество чисел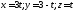 ,
зависящее от параметра
,
зависящее от параметра
t, решением данной системы линейных уравнений

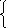
28. К какой из данных систем можно применить метод Крамера
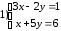

Определив эту систему, решите её.
29. Решить данные системы методом Крамера
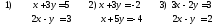


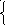
Сделать проверку полученных результатов.
30. Записать данные системы уравнений в матричном виде
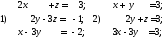
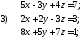
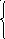
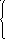
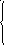
31. Решить системы матричным методом
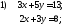
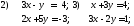
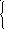

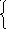
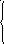
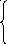
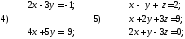
Сделать проверку полученных результатов. 
32. Решить системы линейных алгебраических уравнений матричным методом и методом
Крамера
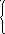

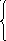
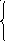
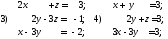
Если количество уравнений в системе не совпадает с числом неизвестных или определитель главной матрицы равен нулю, то решить такую систему методом Крамера или матричным методом невозможно. В этом случае система либо несовместна, ( не имеет решения), либо неопределенна ( имеет бесконечно много решений). Для решения таких систем используют метод Гаусса или его модификацию.
33. Решить систему линейных уравнений ступенчатого вида
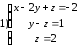
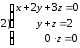
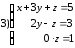
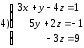
Метод Гаусса заключается в приведении системы линейных уравнений к ступенчатому виду и затем её решение.
Решение систем линейных алгебраических уравнений методом Гаусса.
34. Для данных систем уравнений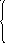
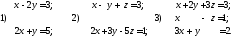


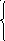
написать расширенные матрицы.
35. По данным расширенным матрицам


написать задающие их системы уравнений.
36. Доказать, что данные системы уравнений равносильны
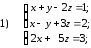
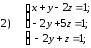
37. Решить данные системы уравнений методом Гаусса
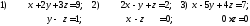
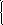
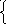

38. Решить
данные системы методом Гаусса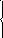

1)
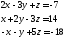 2)
2)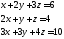
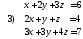
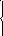
39. Решить данные системы методом Гаусса
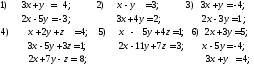

Элементы векторной алгебры и аналитической геометрии
Прямая линия на плоскости.
40.
Написать уравнение
горизонтальной прямой линии проходящей
через точку
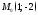 .
.
41. Написать уравнение
вертикальной прямой проходящей через
точку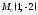 .
.
Написать уравненияпрямой линии:
проходящей через точку
 и имеющей угловой коэффициент
и имеющей угловой коэффициент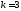 ;
;
2) проходящей через точку
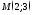 и
имеющей угловой коэффициент
и
имеющей угловой коэффициент
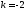 ;
;
3) проходящей
через точку
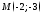 параллельно оси
ОХ;
параллельно оси
ОХ;
4) проходящей через точку
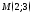 параллельно оси
ОУ;
параллельно оси
ОУ;
5) проходящей
через точки
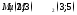 ;
;
6) переписать уравнение прямой
линии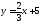 в общем виде;
в общем виде;
7) переписать
общее уравнение прямой линии
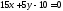 в виде уравнения
в виде уравнения
с угловым коэффициентом.
На прямой линии
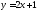 найти точки: 1) у которой абсцисса
найти точки: 1) у которой абсцисса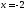 ;
2) у которой ордината
;
2) у которой ордината ;
3) Лежат ли точки
;
3) Лежат ли точки на
прямой
на
прямой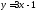 .
.Написать уравнение прямой линии проходящей через точку
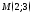 параллельно
параллельно
прямой линии
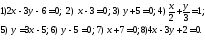
Написать уравнение прямой линии проходящей через точку
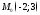 и
и
перпендикулярно прямой линии:
1)
 2)
2)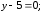 3)
3)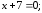 4)
4)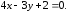
Дать эскизы графиков прямых
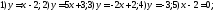
Используя калькулятор вычислить угол наклона прямых линий
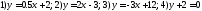
Найти точки пересечения прямой линии
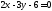 с осями ОХ, ОУ.
с осями ОХ, ОУ.Найти точки пересечения прямых линий. Сделать чертёж.
 ;
;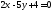 ,
, ;
;
3)
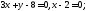
НАЙТИ КООРДИНАТЫ ВЕРШИН ТРЕУГОЛЬНИКА
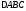 СО
СТОРОНАМИ ОПРЕДЕЛЯЕМЫМИ УРАВНЕНИЯМИ
СО
СТОРОНАМИ ОПРЕДЕЛЯЕМЫМИ УРАВНЕНИЯМИ
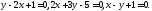
Найти уравнения прямых, на которых лежат стороны
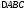 ,
имеющего вершины
,
имеющего вершины
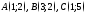 .
.
Найти острый угол между прямыми линиями:
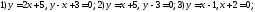
Определить какие из точек
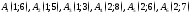
лежат выше прямой, на прямой и ниже
прямой, проходящей через точки
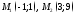 .
.
Напомним, что если точка лежит на прямой линии, то координаты точки являются решением уравнения прямой.
Даны уравнения сторон четырёхугольника
 Найти
уравнения его диагоналей.
Найти
уравнения его диагоналей.Найти абсциссу
 ,
чтобы четырёхугольник с вершинами
,
чтобы четырёхугольник с вершинами
 был
параллелограммом.
был
параллелограммом.Доказать, что диагонали четырёхугольника с вершинами
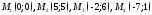 взаимно перпендикулярны.
взаимно перпендикулярны.Используя калькулятор вычислить расстояние от начала координат до прямой
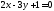 .
.Используя калькулятор вычислить расстояние от точки
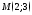 до прямой
до прямой
 .
.Даны вершины
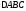 :
: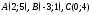 .Найти
: 1) уравнение стороны
.Найти
: 1) уравнение стороны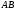 ;
2) уравнение высоты
;
2) уравнение высоты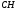 ;
3) уравнение медианы
;
3) уравнение медианы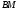 ;
4)точку пересечения высоты
;
4)точку пересечения высоты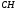 и
медианы
и
медианы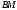 ;
5) уравнение прямой, проходящей через
вершину
;
5) уравнение прямой, проходящей через
вершину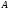 параллельно стороне
параллельно стороне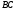 ;
6) длину высоты
;
6) длину высоты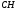 ;
7) величины углов
;
7) величины углов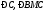 .
.Найти точку
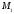 симметричную
точке
симметричную
точке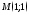 относительно
прямой
относительно
прямой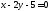 .
.
Кривые второго порядка
Парабола.
Написать уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена в правой полуплоскости симметрично относительно оси ОХ и её параметр равен 3.
Определить величину параметра и дать эскизы парабол
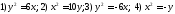
Определить величину параметра, фокус, директрису и дать эскиз.
1)
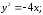 2)
2)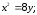 3)
3)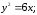 4)
4)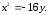
Написать уравнение параболы, которая имеет фокус
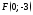 и
вершину в начале координат.
и
вершину в начале координат.
Написать уравнение параболы, которая имеет фокус
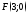 и
вершину в начале координат.
и
вершину в начале координат.Написать уравнение параболы, у которой фокус
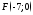 и
уравнение директрисы
и
уравнение директрисы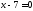 .
.Написать уравнение параболы с вершиной
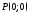 и осью симметрии
и осью симметрии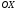 .
Парабола проходит через точку
.
Парабола проходит через точку
1) 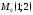 ;
2)
;
2)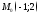 .
.
Написать уравнение параболы с вершиной
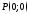 и осью симметрии
и осью симметрии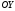 .
Парабола проходит через точку
.
Парабола проходит через точку
1)  ;
2)
;
2)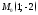 .
.
69. Найти точки пересечения прямой и параболы:
1)
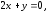
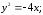 2)
2)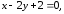
Окружность
70. Написать уравнение окружности, зная
её центр О
 и
радиус
и
радиус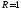 ;
2) её центр О
;
2) её центр О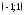 и
радиус
и
радиус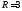 ;
;
71.
Найти точки пересечения окружности
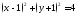 с
осями координат.
с
осями координат.
Эллипс.
72. Написать канонические уравнение эллипса, фокусы которого лежат на оси
абсцисс симметрично относительно начала координат, зная, что
его полуоси равны
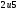 ;
;его большая полуось равна 5, а расстояние между фокусами
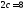 ;
;расстояние между его фокусами
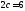 ,
а эксцентриситет
,
а эксцентриситет ;
;расстояние между его директрисами равно 5 и расстояние между
фокусами
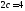 .
.
73. Написать канонические уравнение эллипса, фокусы которого лежат на оси ординат симметрично относительно начала координат, зная, что
1) его полуоси равны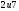 ;
;
его большая полуось равна 10, а расстояние между фокусами
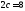 ;
;расстояние между его фокусами
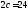 ,
а эксцентриситет
,
а эксцентриситет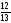 ;
;расстояние между его директрисами равно
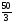 и расстояние между
и расстояние между
фокусами
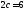 ;
;
74. Дан эллипс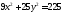 .
Найти его
.
Найти его
полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис.
Дать эскиз.
75. Дать эскиз графика кривой и указать, что это за кривая
1)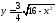 ;
2)
;
2)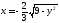
76. Ординату каждой точки окружности с центром в начале координат и радиусом равным 1.
уменьшили в 3 раза. Назвать полученную кривую, определить её параметры и сделать
эскиз её графика.
77. Абсциссу каждой точки окружности с центром в начале координат и радиусом равным 1.
уменьшили в 2 раза. Назвать полученную кривую, определить её параметры и сделать
эскиз её графика.
78. Даны фокусы эллипса
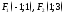 .
Написать уравнения осей его симметрии.
.
Написать уравнения осей его симметрии.
79. Даны: уравнение директрисы
параболы
 и её фокус
и её фокус
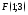 .
Написать уравнения
.
Написать уравнения
осей симметрии параболы.
Гипербола.
80. Написать уравнение гиперболы, фокусы которой расположены на оси абсцисс симметрично относительно начала координат, зная, что
её полуоси
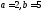 ;
;её горизонтальная ось 8 , а расстояние между фокусами
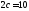 ;
;расстояние между её фокусами
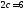 ,
а эксцентриситет
,
а эксцентриситет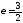 ;
;расстояние между её директрисами равно
 и расстояние между
и расстояние между
фокусами 2с=26;
81. Написать уравнение гиперболы, фокусы которой расположены на оси ординат симметрично относительно начала координат, зная, что
её полуоси равны
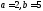 ;
;её действительная полуось равна 4, а расстояние между фокусами
 ;
;расстояние между её фокусами
 ,
а эксцентриситет
,
а эксцентриситет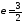 ;
;расстояние между её директрисами равно
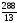 и расстояние между
и расстояние между
фокусами2с=26;
82. Дано уравнение гиперболы
 .
Найти её
.
Найти её
полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис; 5) уравнение асимптот.
83. Пусть задано уравнение кривой второго
порядка:
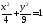 .
Если у кривой есть асимптоты, то написать
их уравнения. Определить:
.
Если у кривой есть асимптоты, то написать
их уравнения. Определить: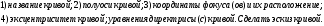
84. Пусть задано уравнение кривой второго
порядка: .
Если у кривой есть асимптоты, то написать
их уравнения. Определить:
.
Если у кривой есть асимптоты, то написать
их уравнения. Определить: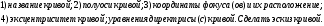
85. Пусть задано уравнение кривой второго
порядка: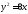 .
Если у кривой есть асимптоты, то написать
их уравнения. Определить:
.
Если у кривой есть асимптоты, то написать
их уравнения. Определить:
86. Определить тип кривой и дать эскиз её графика :
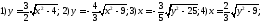
87. Определить, на какой из координатных осей лежат фокусы данных кривых второго
порядка
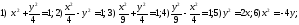
Кривые в полярной системе координат.
89. Построить точки, если заданы их полярные координаты
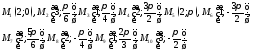
90. Пусть точки заданы в полярной системе координат. Используя калькулятор вычислить, декартовы координаты этих точек
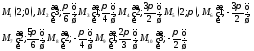
91. Пусть точки заданы в декартовой системе координат. Используя калькулятор вычислить, полярные координаты точек
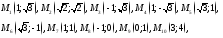
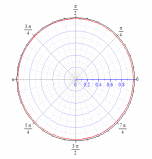
92. Построить кривые в полярной системе координат
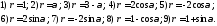
93. Записать уравнения кривых в полярной системе координат
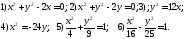
94. Определить точки пересечения кривых
1)
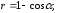
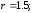 2)
2)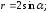
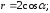
3)
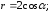
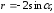 4)
4)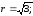
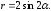
Элементы векторной алгебры
95. Написать координаты двух единичных векторов, которые лежат в плоскости
ОХУ и параллельны прямой линии:
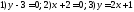 .
.
96. Написать координаты двух единичных векторов, которые лежат в плоскости
ОХУ и перпендикулярны прямой
линии: 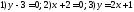 .
.
97. Изобразить на чертеже линейные
комбинации векторов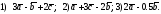
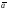
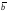
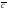

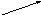

98.
Вычислить линейные комбинации
векторов
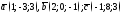
1)
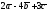 ;
2)
;
2)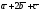 ;
3)
;
3)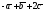
99. Среди указанных пар векторов выбрать коллинеарные векторы
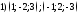 ;
;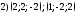 ;
;
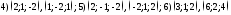
100. Даны три вершины параллелограмма
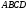 :
:
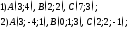
Найти вершину D.
101. Найти четвёртую вершину каждого из трёх параллелограммов, имеющих вершины
 .
.
102. Вычислить:
Единичный вектор в направлении вектора

Вектор длины 3 в направлении вектора
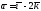
Вектор длины 2 в направлении противоположном направлению
вектора
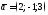
103. Проверить лежат ли точки
 на одной прямой
на одной прямой
104. Решить уравнения
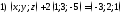 ; 2)
; 2)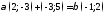
105. Используя калькулятор, вычислить
расстояние от точки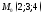 до
до

106. В треугольнике
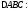
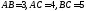 .
Найти
.
Найти
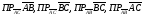
107. В
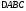 угол С прямой. ВМ- медиана треугольника.
АС=6.
угол С прямой. ВМ- медиана треугольника.
АС=6.
Найти
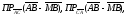
108. В
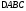 ,
,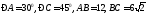 . Используя калькулятор вычислить:
. Используя калькулятор вычислить: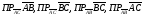 .
.
109. Концы отрезка
 заданы
координатами
заданы
координатами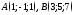 .
На отрезке
.
На отрезке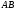
взята точка
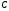 так,
что отрезок
так,
что отрезок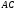 короче
отрезка
короче
отрезка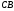 в два раза. Найти
в два раза. Найти
координаты точки
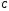 .
.
110. Найти координаты конца отрезка
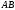 ,
если известны координаты его начала
,
если известны координаты его начала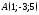 и
его середины
и
его середины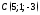 .
.
111. Даны две точки
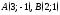 .
Найти координаты точки
.
Найти координаты точки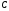 ,
симметричной точке
,
симметричной точке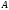 относительно точки
относительно точки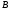 .
.
112. Даны две точки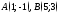 .
Найти координаты точки
.
Найти координаты точки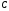 ,
симметричной точке
,
симметричной точке
 относительно точки
относительно точки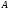 .
.
113 . Найти проекции вектора силы на направление, если заданы: величина силы и угол
между вектором силы и направлением

114. Найти проекции вектора силы на оси координат, если заданы: величина силы
и угол между
вектором силы и осями координат
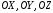
1)

2)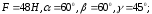
3)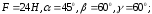
Чему равны координаты вектор
силы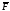 ?
?
115. Найти проекции вектора силы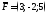 на оси координат.
на оси координат.
116. Точки
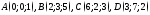 являются вершинами пирамиды
являются вершинами пирамиды
найти: 1)
середину рёбер
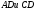 ;
2) расстояние между этими серединами;
;
2) расстояние между этими серединами;
3) проекцию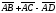 на
оси координат; 4) длину вектора
на
оси координат; 4) длину вектора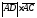 ;
;
Скалярное произведение векторов
Контрольные вопросы
1)Что можно сказать о векторах,
если
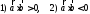
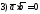 ;
;
2) Что можно сказать о не нулевых
векторах, если
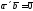 ;
;
3) Что можно сказать о не нулевых
векторах, если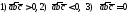
117. Вычислить скалярное произведение
векторов
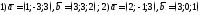 .
3)
.
3)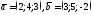
118. Среди векторов

определить взаимно перпендикулярные векторы.
119. При каком параметре
 ,
векторы
,
векторы
взаимно перпендикулярны.
120. Пусть даны два вектора
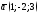 ,
,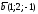
требуется вычислить
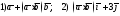 .
.
121. Используя скалярное произведение, вычислить:
1) проекцию вектора на вектор
на вектор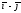 ;
;
2) угол между векторами
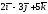 И
И ;
;
122. Пусть
задан вектор силы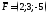 .
Определить величину усилия от действия
.
Определить величину усилия от действия
силы
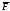 в
заданных направлениях : 1)
в
заданных направлениях : 1)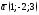 ;
2)
;
2)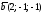 ;
3)
;
3)
123. Какие
углы образует вектор
 с осями координат.
с осями координат.
124. Постоянная сила
 приложена
к телу и перемещает его вдоль отрезка
приложена
к телу и перемещает его вдоль отрезка
прямой из точки
 .
Вычислить работу силы.
.
Вычислить работу силы.
125. Вычислить работу постоянной
вектор-силы
 действующей
вдоль
действующей
вдоль
отрезка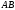 от
от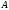 к
к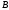 ,
где 1)
,
где 1) 2)
2)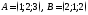 .
.
Векторное произведение векторов
126. Вычислить определители:

127. Для векторов
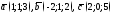 вычислить векторные произведения:
вычислить векторные произведения:

128. Найти вектор перпендикулярный
двум векторам
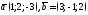 ;
;
129.
Вычислить площадь
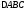 ,
где:
,
где:
1)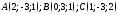
2)

130. Вычислить момент силы
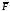 ,
приложенной в точке
,
приложенной в точке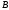 ,
относительно точки
,
относительно точки
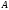
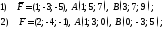
131. Найти все единичные вектора
перпендикулярные векторам
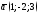 ,
,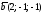 .
.
132. Найти все векторы перпендикулярные
векторам
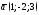 ,
,
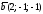 .
.
133. Для векторов:
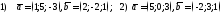
проверить равенство
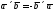 .
.
134. Найти вектор перпендикулярный
плоскости
 ,
где
,
где
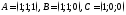
135. Вычислить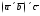 ,
где
,
где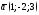 ,
,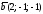 ,
,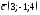
Смешанное произведение векторов.
136. Для векторов
 вычислить смешанное произведение
вычислить смешанное произведение
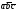 .
.
137. Вычислить объём пирамиды, если известны координаты её вершин
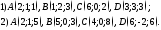
138. Проверить являются ли данные векторы компланарными:
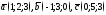
139. Лежат ли точки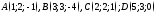 в одной и той же плоскости?
в одной и той же плоскости?
Плоскости и прямые в пространстве
Контрольные вопросы
Среди данных утверждений найти верные утверждения:
1) Прямая и плоскость только параллельны либо перпендикулярны;
2) Две прямые в пространстве либо параллельны, либо пересекаются;
3) Две плоскости перпендикулярные к данной прямой перпендикулярны;
4) Две плоскости перпендикулярные к данной прямой параллельны;
5) Две прямые параллельные к плоскости параллельны между собой;
6) Две прямые параллельные к плоскости перпендикулярны между собой;
7) Две плоскости параллельные к третьей параллельны между собой;
8) Две плоскости параллельные к третьей перпендикулярны между собой;
9) Существует прямая, пересекающая плоскость ровно в двух точках.
140. Написать уравнения плоскостей, удовлетворяющих условиям:
1) плоскость проходит через точку
 перпендикулярно
нормальному вектору
перпендикулярно
нормальному вектору
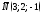 ;
;
2) плоскость проходит через точку
 параллельно
плоскости
параллельно
плоскости ;
;
3) плоскость проходит через точку
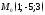 параллельно
векторам
параллельно
векторам
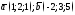 ;
;
4) плоскость проходит через точки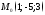 ,
,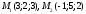 ;
;
141. Написать уравнения плоскостей, удовлетворяющих условиям:
1) плоскость проходит через точку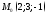 перпендикулярно нормальному
перпендикулярно нормальному
вектору
 ;
;
2) плоскость проходит через точку
 параллельно
плоскости
параллельно
плоскости
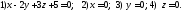
3) плоскость проходит через
точку
 параллельно
векторам
параллельно
векторам
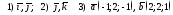
4) плоскость проходит через
точки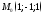 ,
,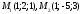 .
.
5) плоскость проходит через
начало координат и точку
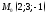 параллельно
параллельно
вектору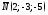 .
.
142. Среди указанных плоскостей выделить:
1. параллельные плоскости:
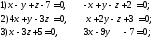
2. перпендикулярные плоскости:
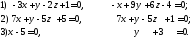
143. Определить углы между
нормальным вектором к плоскости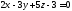
и осями координат.
144. Определить углы между плоскостями
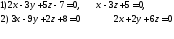
145. Найти расстояние от точки
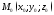 до
плоскости
до
плоскости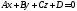
1) Найти расстояние от точки
 до
плоскости
до
плоскости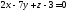 ;
;
2) Найти расстояние от точки
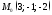 до плоскости
до плоскости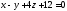 ;
;
146. Определить точку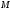 симметричную
точке
симметричную
точке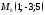 относительно
относительно
плоскости
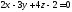 .
.
147. Составить параметрические уравнения прямой линии, проходящей через точку
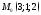 и
и
параллельно вектору
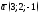 ,
2) параллельно прямой линии
,
2) параллельно прямой линии
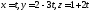 ,
3) параллельно оси ОУ, 4) перпендикулярно
плоскости
,
3) параллельно оси ОУ, 4) перпендикулярно
плоскости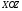 ,
5) перпендикулярно плоскости
,
5) перпендикулярно плоскости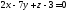 ,6)
точку
,6)
точку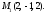
148. Среди указанных прямых выделить:
1. параллельные прямые:
1)
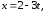

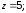 2)
2)
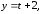
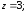
3)
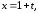
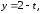
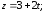 4)
4)
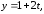
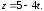
2. перпендикулярные прямые:

149. Вычислить угол между прямыми
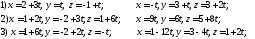
150. Составить параметрические уравнения прямой, являющейся пересечением двух
плоскостей:
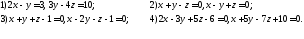
151. Вычислить угол между прямыми 1) и 2), 3) и 4) заданными общими уравнениями
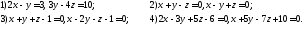
152. Определить точку М симметричную
точке
 относительно
прямой линии
относительно
прямой линии

153. Определить взаимное расположение прямой и плоскости и если они
пересекаются найти координаты точки пересечения
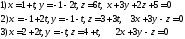

154. Вычислить угол между прямой и плоскостью

155. Написать уравнение
плоскости проходящей через точку
перпендикулярно прямой:

156. Написать параметрические уравнения прямых линий являющихся
пересечениями плоскости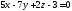 с координатными плоскостями.
с координатными плоскостями.
Введение в математический анализ
157. Используя калькулятор,
вычислить значения функции
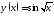 в
точках:
в
точках:
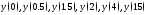
158.
Используя калькулятор, вычислить
значения функции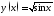 в
точках:
в
точках:
 .
.
159. Вычислить
 ,если
:
,если
: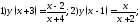
160. Найти области задания функций

161. Найти области задания функций
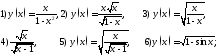
162. Найти
область значений функций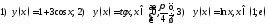
163. Найти область значений функций
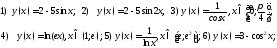
164. Какое утверждение из двух следующих верно
1) каждой абсциссе графика соответствует одна ордината
2) каждой ординате графика соответствует одна абсцисса
165.
1. По данному графику найти ординаты
точек, если их абсциссы равны
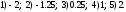
2. По данному графику найти абсциссы точек, если их ординаты равны


166.
По
таблицам построить графики функций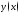
|
Х |
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
|
У |
0,2 |
0,31 |
0,5 |
0,8 |
1 |
0,8 |
0,5 |
0,31 |
0,2 |
0,16 |
|
Х |
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
|
У |
2,24 |
2,12 |
2,0 |
1,87 |
1,73 |
1.58 |
1,41 |
1,22 |
1 |
0,7 |
167. Используя калькулятор, заполнить таблицу и по ней построить график
функции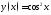
|
Ххх х |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1. |
1.1 |
1.2 |
1.3 |
1.4 |
1.5 |
1.6 |
1.7 |
|
у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
168. Среди предложенных функций указать равные функции
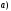
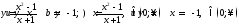
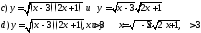
169. Среди предложенных функций указать равные функции
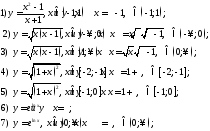
170. Функции
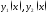 определены
на множестве
определены
на множестве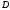 ,
симметричном
относительно начала координат. Будет
ли чётной функция:
,
симметричном
относительно начала координат. Будет
ли чётной функция:

171. Функции
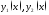 определены
на множестве
определены
на множестве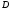 ,
симметричном относительно
начала координат. Будет ли нечётной
функция:
,
симметричном относительно
начала координат. Будет ли нечётной
функция:

172. Среди заданных функций выделить чётные и нечётные функции
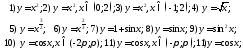
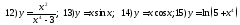 ;
;
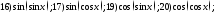
173. Вычислить нули данных функций

174.
Доказать, что функция
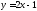 возрастает,
а функция
возрастает,
а функция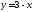 убывает.
убывает.
175. Среди данных функций указать возрастающие и убывающие функции
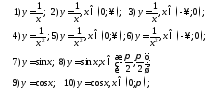
176. Проверить по определению, что данная функция
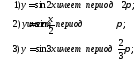
177. Выделяя полный квадрат, вычислить экстремумы функций
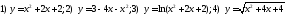
178. Используя калькулятор вычислить значения функций
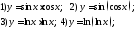
в точках
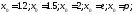
179. Используя
графики функций
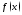 (рис.1)
и
(рис.1)
и
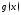 (рис.2),
приближённо вычислить
(рис.2),
приближённо вычислить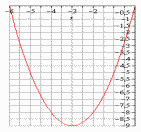
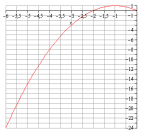
рис.1 рис.2
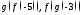 .
.
180. Пусть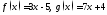 ..
Написать выражения для функций
..
Написать выражения для функций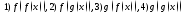 .
.
181. Пусть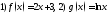 .
Написать выражения для функций
.
Написать выражения для функций
 .
.
182. Пусть
 .
Написать выражения для функций
.
Написать выражения для функций
 .
.
183. Проверить, является ли функция
 обратной
относительно функции
обратной
относительно функции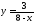 .
.
184. Проверить, является ли функция
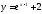 обратной
относительно функции
обратной
относительно функции
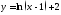 .
.
185. Написать формулы для функций обратных к данным
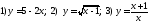 ;
; .
.
Предельные значения функции
186. Пусть переменная
 удовлетворяет неравенству
удовлетворяет неравенству
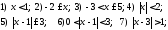
На числовой прямой укажите
интервалы, которым принадлежит
переменная .
.
187. Пусть
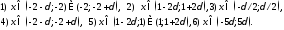
а) К какому числовому значению
стремится переменная
 ,
если параметр
,
если параметр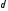
неограниченно уменьшается до нуля.
б) В каком из случаев1)-6)
 может
принимать это предельное значение.
может
принимать это предельное значение.
188. Пусть абсцисса графика
функции
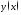 стремится:
1) к
стремится:
1) к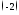 слева,
2) к
слева,
2) к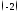 справа
справа
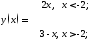
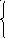
Определить по графику
 .
Существует ли
.
Существует ли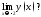
Пусть аргумент
 функции
функции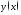 стремится
слева к точке
стремится
слева к точке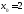 ,
принимая значения:
,
принимая значения:
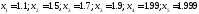 .
Используя калькулятор, спрогнозируйте,
к чему стремятся соответствующие
значения функции
.
Используя калькулятор, спрогнозируйте,
к чему стремятся соответствующие
значения функции
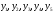 , если
, если
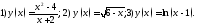
Пусть аргумент
 функции
функции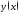 стремится
справа к точке
стремится
справа к точке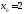 ,
принимая значения:
,
принимая значения:
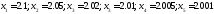 .
Используя калькулятор, спрогнозируйте,
к чему стремятся соответствующие
значения функции
.
Используя калькулятор, спрогнозируйте,
к чему стремятся соответствующие
значения функции
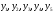 , если
, если
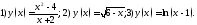
Проверить, используя график, функции: существует ли предельные значения данных функций
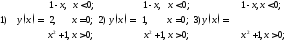
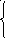
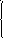
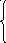
при стремлении аргумента к 0.
к 0.
192.
Пусть 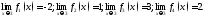
Вычислить
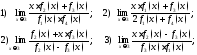
193. Пусть 
Вычислить
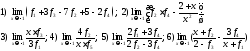
194. Пусть
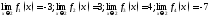 .
.
Вычислить
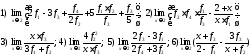
195. Используя график функции вычислить приближенно значения функций, левые и
правые предельные значения
функций в точке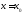
1)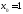 2)
2)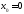 3)
3)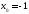
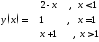
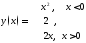
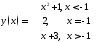
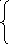
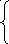
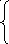
196. Пусть
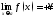 .
Вычислить предельные значения
.
Вычислить предельные значения
 .
.
197. Пусть
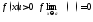 .
Вычислить предельные значения
.
Вычислить предельные значения
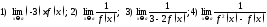 .
.
198. Пусть
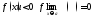 .
Вычислить предельные значения
.
Вычислить предельные значения
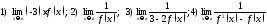 .
.
Вычислить левые и правые предельные значения следующих функций.
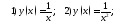
Написать уравнения их горизонтальных и вертикальных асимптот.
При вычисления следующих пределов используйте правило
Правило 1. Для любой элементарной
функции
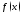 справедлива
формула если
справедлива
формула если ,то
,то
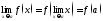 ;
;
200. Вычислить указанные пределы и значения функции в предельных точках
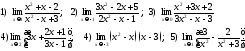

201. Вычислить указанные пределы

202. Вычислить указанные пределы
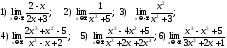
203.
Вычислить указанные пределы
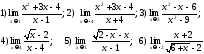

204. Дайте определение горизонтальной асимптоты графика и найдите уравнения горизонтальных асимптот графиков данных функций.

205. Дайте определение вертикальной асимптоты графика и найдите уравнения вертикальных асимптот графиков данных функций

Непрерывность и разрывы функций
206. Пусть функции
 определены на интервале
определены на интервале и их сумма
и их сумма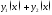 и их разность
и их разность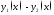 являются
непрерывными функциями. Доказать, что
тогда функции
являются
непрерывными функциями. Доказать, что
тогда функции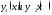 являются
непрерывными.
являются
непрерывными.
207. Указать интервалы на оси ОХ, в которых данные функции непрерывны

208. При каком значении параметра
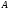 данные функции
данные функции непрерывны
непрерывны
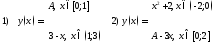
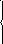

209. Исследовать данные функции на непрерывность
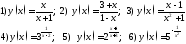
210. Исследовать данные функции на непрерывность и дать эскизы графиков
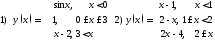
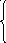
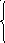
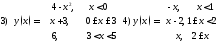

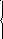
211. Среди данных интервалов 
указать интервалы, в которых
функция
 достигает
своих
достигает
своих
наибольшего и наименьшего значений.
212. Доказать что данные функции непрерывны, дать эскизы графиков и по ним
найти наибольшее и наименьшее значения функций

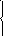
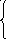

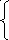
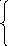
213. Исследовать данную функцию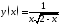 на непрерывность
на непрерывность
на множествах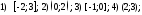
214. Доказать, что любой кубический многочлен имеет по крайней мере
один ноль.
Замечательные пределы
215. Используя замечательные пределы найти предельные значения выражений
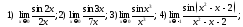
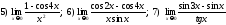 ;
;
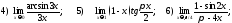
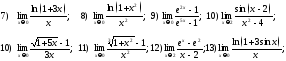
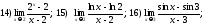
216. Используя второй замечательный предел найти предельные значения выражений

217. Вычислить указанные пределы
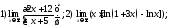
218. Вычислить указанные пределы:
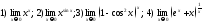
Дифференцирование. Определения. Основные правила.
219. Вычислить приращение функции
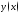 в
точке
в
точке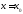

Используя определение производной функции и соответствующие замечательные пределы, вычислить производные данных функций
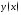 :
: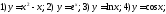
Написать уравнение касательной и нормальной прямой к функции
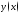
в точке
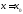 :
:
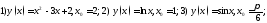
Найти точки пересечения полученных касательных с осями координат.
222.
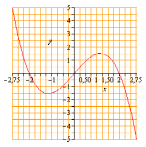
По данному графику функции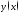 написать
приближённо уравнения касательных к
графику в точках заданных координатами
написать
приближённо уравнения касательных к
графику в точках заданных координатами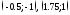 .
.
223. Найти угол между касательными,
проведенными в точках
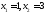
к графику функции
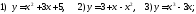
224. Найти угол между графиками функций и осью ОХ в указанных точках
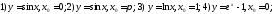
225 . Найти острый угол между
графиками функций
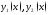 в
точке
в
точке
их пересечения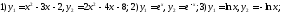
226. По оси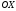 движется
точка, абсцисса которой с течением
движется
точка, абсцисса которой с течением
времени изменяется по
закону
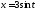 +2.
Определим абсциссу точки и её
+2.
Определим абсциссу точки и её
скорость и ускорение в
моменты времени: 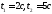 .
Определить
.
Определить
моменты времени, когда усилие, действующее на точку равно: 1) нулю,
2) максимально.
227. Пусть материальная точка движется
вдоль оси ОХ по закону
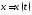 ,
где
,
где
 -
время:
-
время:
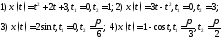
А. Вычислить среднюю
скорость за промежуток времени
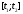 .
.
В.вычислить мгновенную
скорость точки в моменты времени
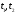
228. Найти координаты материальных точек, движущихся по закону
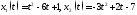 ,
в момент времени когда
,
в момент времени когда
их скорости совпадают.
229. Вычислить производные функций
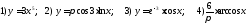
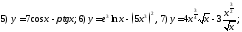
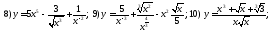
230. Вычислить производные функций
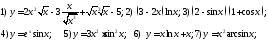

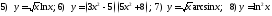
231. Вычислить производные функций
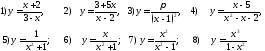
232 .
Используя калькулятор, вычислить
производные функций в точке
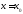
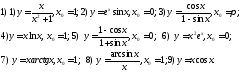
233. Найти функцию по заданной производной. Сделать проверку
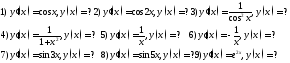
234. Доказать, что данная
функция: 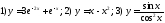
обращает соответствующее уравнение в тождество:
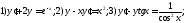
235. Найти вторые производные заданных функций
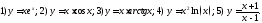
236. Доказать, что функция
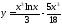 превращает
уравнение
превращает
уравнение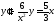
в тождество.
Дифференцирование функции от функции.
237. Применив цепное правило вычислить производные функций
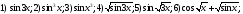
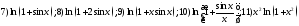 ;
;
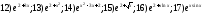 ;
;
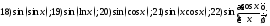
23)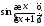
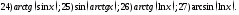
238. Используя калькулятор, вычислить производные функций в заданной точке
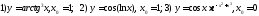
239. Вычислить угол между
касательными к функции
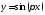 , проведёнными в
, проведёнными в
точках:
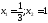
240. Используя равенства
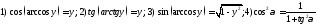
доказать формулы 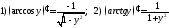
Логарифмическое дифференцирование
241. Вычислить производные заданных функций
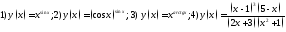
Формулы неявного дифференцирования
242. Доказать, что данные формулы задают одну и туже кривую линию

243. Применяя правило неявного дифференцирования, вычислить
производные от функций заданных неявно (уравнениями)

244. Найти вторую производную
функции заданной
заданной
неявно (уравнениями)
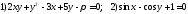 ;
;
Формулы параметрического дифференцирования
245. Вычислить и записать в
параметрическом виде производные
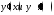 от
от
функции
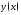 заданной
в параметрическом виде
заданной
в параметрическом виде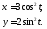

Вычислить и записать в параметрическом виде первую и вторую производные
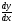 и
и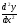 от
функций
от
функций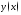 заданных
в параметрическом виде
заданных
в параметрическом виде
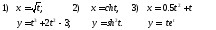 4)
4)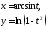


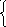

Написать уравнение касательной и нормали к кривым заданным
неявно (уравнениями) в точке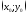
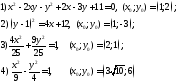
Написать уравнение касательной и нормали к кривым заданным
параметрическими уравнениями
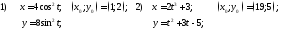
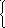

Дифференциал функции
249. Используя таблицу найти
дифференциалы следующих функций
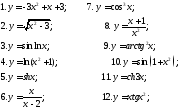
Вычислить дифференциал дуги графиков функций

251. Изобразить геометрически приращение функции и дифференциал функции
при заданных величинах
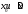 .
Оценить погрешность по графику
.
Оценить погрешность по графику
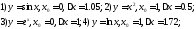
252. Используя понятие дифференциала получите приближённые формулы,
справедливые для малых

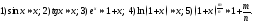
253. Используя формулу линейного
приближения функции , оценить максимальную
погрешность при вычислении
значения выражения
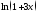 ,
при
,
при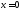 ,если
аргумент
,если
аргумент задан
приближённо
задан
приближённо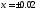 .
.
254. Используя формулу линейного приближения функции , оценить максимальную
погрешность при вычислении
значения выражения ,
при
,
при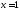 ,если
,если
аргумент
 задан
приближённо
задан
приближённо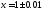 .
.
255. Вычислить значение данного выражения двумя способами: а) используя
калькулятор и в) используя формулу линейного приближения функции
1)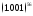 (взять
(взять )
3)
)
3)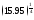 (взять
(взять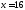 )
)
2)
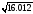 (взять
(взять );
4)
);
4)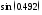 (взять
(взять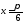 ;
;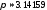 ;
;
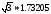 ).
).
256. Приближенно измеренный радиус
круга оказался равным 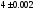 м.
м.
Используя формулу линейного приближения , оценить какова будет максимальная ошибка при вычислении
1) площади круга, 2) длины окружности.
257. Приближенно измеренный
радиус шара оказался равным 1 м.
м.
используя формулу линейного приближения , оценить какова будет
максимальная ошибка при
вычислении площади поверхности (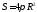 )
)
этого шара. Для расчётов
взять
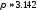 .
.
258. Приближенно измеренное
ребро куба оказался равным
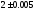 м.
Используя
м.
Используя
формулу линейного приближения, оценить какова будет максимальная ошибка при
вычислении объёма куба и площади поверхности куба.
Правило Лопиталя
259. Написать формулу Лагранжа (о среднем в дифференцировании) для функций
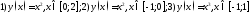
260. Используя правило
Лопиталя, вычислить указанные пределы
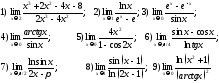
261. Используя правило Лопиталя, вычислить указанные пределы
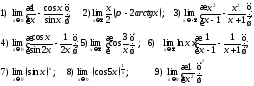
262. Написать уравнения горизонтальных асимптот
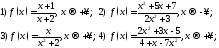
263. Написать уравнения горизонтальных и вертикальных асимптот и дать эскиз
графика функции
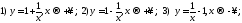
Приложение дифференцирования к задачам геометрии и механики
264. Найти острый угол между касательными
прямыми к параболе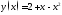 проведёнными в точках графика
проведёнными в точках графика .
.
Найти две касательных к параболе:
 ,
проходящих через начало координат.
,
проходящих через начало координат.Найти точку пересечения касательных прямых проведенных к параболе
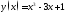 в
точках
в
точках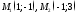 .
.Найти уравнение касательной прямой, проведённой к параболе
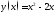 ,
,
параллельной к прямой
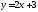 .
.
Найти уравнение касательной прямой, проведённой к параболе
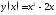 ,
,
перпендикулярной к прямой
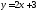 .
.
Найти расстояние от точки
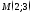 до
касательной прямой, проведённой
до
касательной прямой, проведённой
к параболе
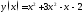 в
точке касания
в
точке касания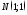 .
.
Найти угол между графиками функций
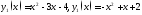
в точке их пересечения.
Под каким углом пересекают ось ОХ синусоиды:
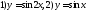
в точках:
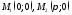
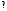
Под каким углом, и в какой точке касательная к кривой
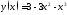 ,
проведённая в точке
,
проведённая в точке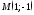 пересекает
ось ОХ
пересекает
ось ОХ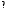
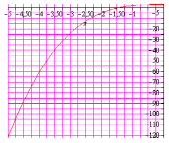
К какому классу монотонных функций принадлежит производная функции. Функция представлена на графике.
274.

К какому классу монотонных функций принадлежит производная функции. Функция представлена на графике.
275. Дать эскиз графика любой функции
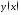 заданной на интервале
заданной на интервале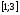 ,
для
,
для
которой
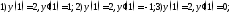
276. Изобразить на графике любую пару
дифференцируемых функций
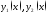 ,
,
для которых 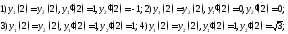
Cколько таких пар функций существует?
277. Секущая графика параболы
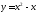 проходит
через точку
проходит
через точку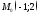 параллельно
касательной, проведённой к параболе в
точке
параллельно
касательной, проведённой к параболе в
точке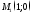 .
Найти
.
Найти
точку пересечения секущей и параболы.
278. Материальная точка движется по
параболе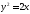 так,
что скорость изменения ординаты
так,
что скорость изменения ординаты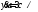 .
Найти мгновенную скорость изменения
абсциссы в точках
.
Найти мгновенную скорость изменения
абсциссы в точках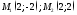 .
.
279. Найти на гиперболе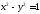 точку, в которой мгновенная скорость
точку, в которой мгновенная скорость
ординаты в два раза больше скорости абсциссы ;
ординаты равна скорости абсциссы ;
ординаты в два раза меньше скорости абсциссы ;
Материальная точка движется по эллипсу
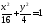 так,
что скорость изменения абсциссы
так,
что скорость изменения абсциссы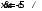 ..
Найти мгновенную скорость изменения
ординаты в
..
Найти мгновенную скорость изменения
ординаты в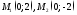 .
.
281. Материальная точка движется вдоль
оси ОХ по закону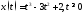 .
.
Найти моменты времени, в которые
скорость точки равна нулю;
сила действующая на точку равна нулю;
точка меняет направление движения;
определить направление движения в
моменты времени
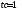 ,
,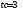 .
.
Исследование функций и построение её графиков
282. Определить интервалы возрастания
и убывания функций 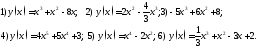
Определить интервалы возрастания и убывания функций

Определить локальные экстремумы функций

Доказать, что функция
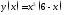 имеет локальный максимум в
имеет локальный максимум в
точке 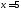 и
не имеет экстремума в точке
и
не имеет экстремума в точке .
.
Доказать, что функция
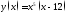 имеет локальный минимум в
имеет локальный минимум в
точке
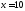 и
не имеет экстремума в точке
и
не имеет экстремума в точке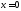 .
.
Определить локальные экстремумы функций
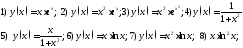
Доказать, что график функции
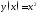 лежит
выше любой своей касательной
лежит
выше любой своей касательной
прямой.
Найти точки перегиба графиков и интервалы выпуклости данных функций
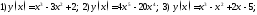
Найти точки перегиба графиков и интервалы выпуклости данных функций
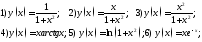
Доказать, что для графика функции
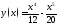 точка
точка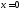 не
является
не
является
точкой перегиба, а точка
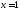 есть
точка перегиба.
есть
точка перегиба.
Найти асимптоты графиков данных функций
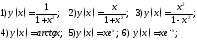
Исследовать данные функции и построить их графики
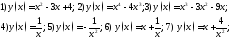
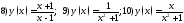
Задачи на нахождение наибольших и наименьших значений функций
Число 8 разбить на два слагаемых так, чтобы их произведение было
наибольшим.
Найти на оси
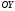 точку,
для которой сумма квадратов расстояний
от точек
точку,
для которой сумма квадратов расстояний
от точек
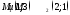 была
бы наименьшей.
была
бы наименьшей.
Среди прямоугольников, имеющих периметр 8м, найти прямоугольник
с наибольшей площадью.
Среди прямоугольных треугольников, имеющих одинаковую гипотенузу
 =10м,
найти треугольник наибольшей площади.
=10м,
найти треугольник наибольшей площади.
Прочность балки прямоугольного сечения прямо пропорциональна ширине
балки и квадрату её высоты. Определить параметры балки наибольшей
прочности, которую можно вырезать из бревна, диаметр которого 0.5м.
Пусть требуется построить цилиндрический бак объёмом
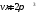 .
Какими
.
Какими
должны быть размеры бака, чтобы на его изготовление ушло как можно
меньше листовой стали. Для расчётов
принять
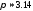 .
.
Из стального листа площадью
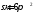 требуется
изготовить цилиндр
требуется
изготовить цилиндр
наибольшего объёма. Определить радиус и высоту такого цилиндра.
Для расчётов принять
 .
.
Среди всех прямых круговых конусов, у которых образующая равна
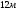 ,
,
найти радиус основания конуса наибольшего объёма.
Кривизна дуги кривой.
Найдите кривизну следующих линий в точке
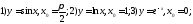
Вычислите кривизну линий в точке
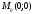
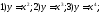
Найдите кривизну параболы в точке
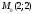
Найдите кривизну равнобочной гиперболы
 в
точке
в
точке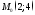
Найдите кривизну циклоиды при значении параметра


ОТВЕТЫ И РЕШЕНИЯ.
1.1
17 1.2 01.3 1 2.1 -12.2 12.3 13.1 93.2 -263.3 -214.0
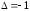
4.1
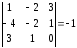 4.2
4.2 5.
5.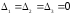 так как в каждом определителе есть
одинаковые строки.
так как в каждом определителе есть
одинаковые строки.
6.1 ;
6.2
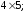
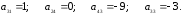

7.1
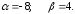 7.2
7.2  7.3
7.3 
8.Нельзя. Матрицы разных размерностей.
9.
1
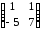 9.2
9.2
 9.3
9.3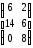 9.4
9.4
10.
 11.
11.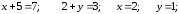
12.
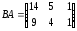 ;
;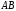 -не существует.
-не существует.
13.1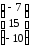 13.2
13.2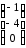 13.3
13.3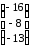 13.4
13.4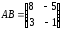 13.5
13.5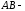 не
существует.
не
существует.
13.6
 13.7
13.7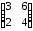 14.1
14.1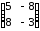 14.2
14.2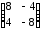 14.3
14.3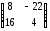
15.1

15.2

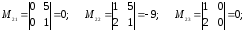

15.3
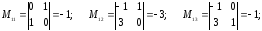


16.1 9 16.2 116.30
17.1
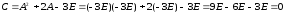
17.2
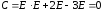
18.
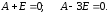 19.
19. 20.Не являются.
20.Не являются.
21. Матрица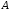 имеет обратную матрицу.
имеет обратную матрицу.
22.1
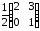 22.2
22.2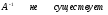 22.3
22.3
23.1
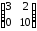 23.2
23.2 23.3
23.3 23.4
23.4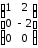
23.5
 24.1
24.1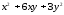 24.2
24.2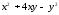
25.1
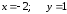 25.2
25.2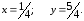 26.Не являются.27. Не являются.
26.Не являются.27. Не являются.
28.1
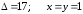 29.1
29.1 29.2
29.2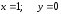
30.1


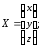
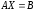
30.2
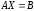 где
где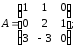
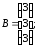
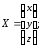
30.3
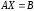 где
где
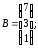
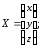
31.1
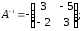
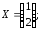 31.2
31.2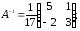
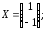
31.3

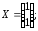 31.4
31.4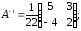
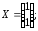
31.5

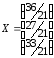 32.1
32.1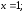
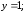
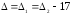
 32.2
32.2
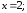
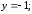


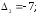
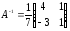
32.3
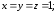
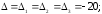

32.4
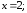
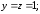
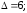
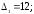
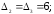
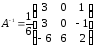
33.1
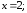

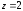 33.2
33.2
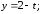
 33.3Система не совместна33.4
33.3Система не совместна33.4
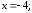
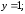
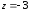
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ МЕТОДОМ ГАУССА.
34.1
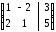 34.2
34.2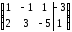
34.3
 35.1
35.1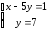 35.2
35.2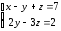 35.3
35.3
35.4
 36
36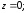
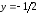 ;
;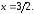 Решения одинаковы.
Решения одинаковы.
37.1
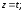
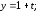
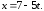 37.2
37.2
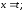
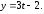 37.3
37.3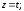
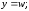
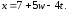
38.1
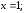
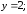
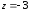 38.2
38.2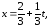
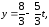
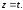 38.3Система не совместна.
38.3Система не совместна.
39.1
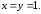 39.2
39.2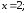
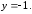 39.3
39.3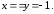 39.4
39.4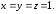
39.5

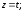
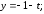
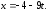 39.6
39.6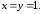
Элементы векторной алгебры и аналитической геометрии.
Прямая линия на плоскости.
40.
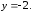 41.
41.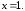 42.1
42.1 42.2
42.2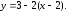 42.3
42.3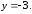
42.4
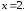 42.5
42.5 42.6
42.6
42.7
 43.1
43.1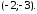 43.2
43.2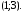 43.3Обе точки принадлежат прямой.
43.3Обе точки принадлежат прямой.
44.1
 44.2
44.2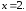 44.3
44.3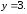 44.4
44.4
44.5
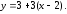 44.6
44.6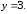 44.7
44.7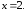 44.8
44.8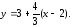
45.1
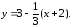 45.2
45.2 45.3
45.3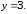 45.4
45.4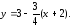
46.1 46.2
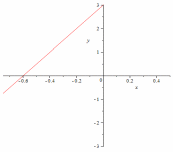
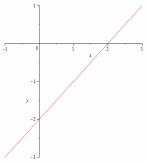
46.4
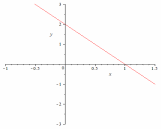

46.5
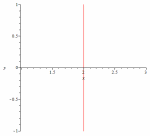
47.1
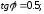
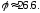 47.2
47.2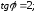
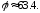 47.3
47.3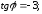
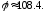
47.4
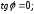
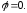 48.
48.
49.1
 49.2(0.5; 1).
49.2(0.5; 1).
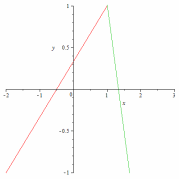
49.3
(2; 2).50.
51.


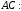
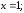
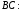
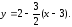
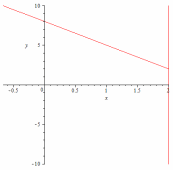
52.1
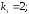
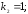
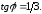
52.2
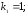
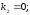
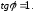
52.3
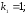

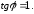
53.
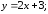 А1 –выше; А2 –на
прямой;
А1 –выше; А2 –на
прямой;
А3 – ниже; А4 –выше; А5 –ниже;
А6 – на прямой.
54.

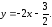
55.
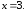 56
56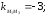
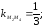
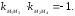

57
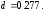 58.
58. 59.1
59.1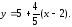 59.2
59.2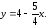
59.3
 59.4
59.4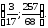 59.5
59.5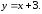 59.6
59.6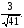
59.7
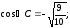
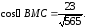 60.
60.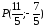 -точка
пересечения перпендикуляра, проходящего
через точку М, с заданной прямой.
-точка
пересечения перпендикуляра, проходящего
через точку М, с заданной прямой.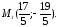
Кривые второго порядка.
Парабола.
61.
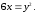
62.1
 62.2
62.2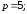
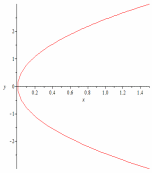
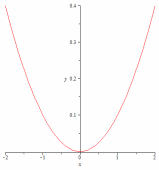
62.3
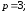 62.4
62.4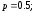
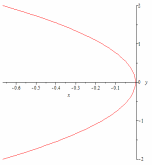
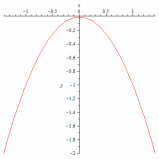
63.1
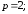

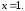 63.2
63.2
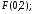
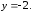

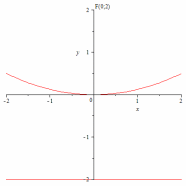
63.3

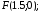
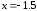 63.4
63.4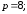
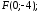
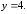
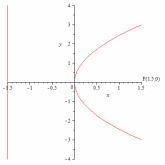
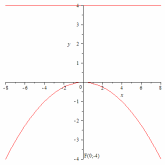
64.
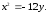 65.
65.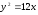 66.
66.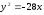 .
67.1
.
67.1 67.2
67.2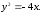
68.1
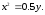 68.2
68.2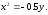 69.1
69.1 69.2Точек нет.
69.2Точек нет.
Окружность.
70.1
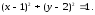 70.2
70.2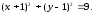 71.
71.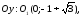
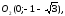
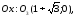

Эллипс.
72.1
 72.2
72.2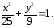 72.3
72.3 72.4
72.4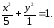
73.1
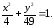 73.2
73.2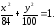 73.3
73.3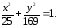 73.4
73.4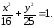
74.
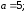
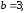
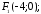
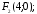
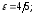

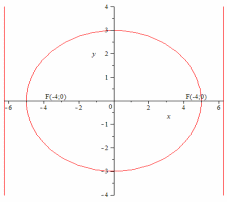
75.2
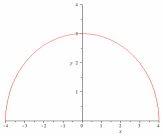
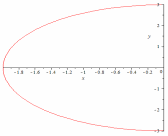
Эллипс.
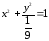 77. Эллипс
77. Эллипс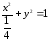
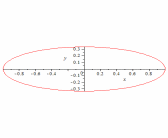
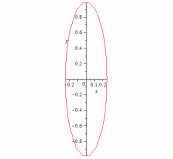
78.
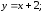
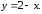 79.
79.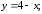
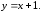
Гипербола.
80.1
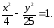 80.2
80.2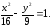 80.3
80.3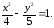 80.4
80.4
81.1
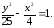 81.2
81.2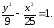 81.3
81.3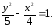 81.4
81.4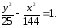
82.


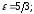
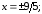
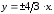
83. Эллипс.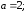
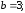
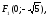 84. Гипербола.
84. Гипербола.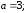
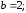
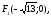
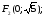
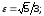
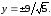

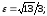
 .
асимптоты:
.
асимптоты: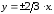
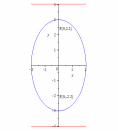

85.
Парабола.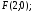
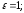 директриса:
директриса: 86.1Гипербола.
86.1Гипербола.
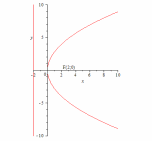
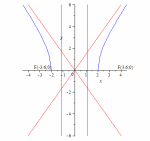
86.2Гипербола86.3Гипербола
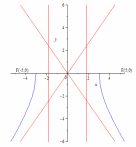
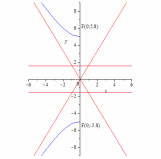
86.4 Гипербола.
 87.1 На оси
Оу.87.2 На оси Ох. 87.3 На оси Ох.87.4 На оси Оу. 87.5 На оси Ох.
87.6 На оси Оу.
87.1 На оси
Оу.87.2 На оси Ох. 87.3 На оси Ох.87.4 На оси Оу. 87.5 На оси Ох.
87.6 На оси Оу.
Кривые в полярной системе координат
89.
90.1 х=2,у=0.90.2
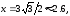
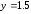 90.3
90.3
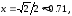
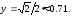 90.4
90.4 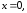
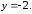 90.5
90.5
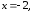
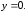 90.6
90.6


90.7 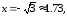
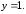 90.8
90.8
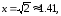
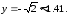
90.9
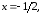
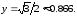 90.10
90.10
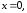
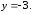 91
91
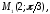
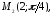
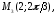

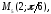
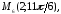
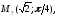
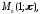
92.1 92.2
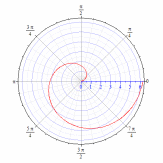
92.4
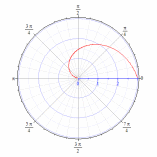
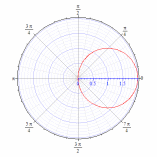
92.5 92.6
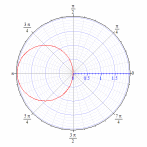
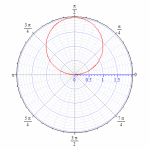
92.7 92.8
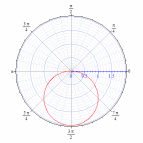
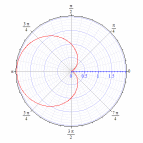
92.9
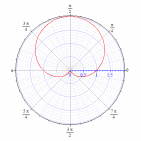
93.1 При замене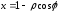 ,
,
 уравнение
уравнение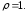
93.2 1 При замене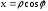 ,
,
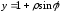 уравнение
уравнение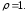
93.3 Парабола.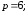
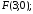
 Формулы перехода:
Формулы перехода:
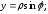 полярная ось направлена вдоль оси Ох;
полюс совпадает с фокусом. При подстановке
в уравнение получаем
полярная ось направлена вдоль оси Ох;
полюс совпадает с фокусом. При подстановке
в уравнение получаем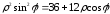 или
или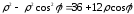 ,
или
,
или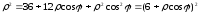 .
Разрешая это уравнение относительно
.
Разрешая это уравнение относительно получаем
получаем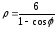 каноническое уравнение параболы в
полярной системе координат.
каноническое уравнение параболы в
полярной системе координат.
93.4 Парабола.
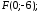
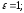 Формулы перехода:
Формулы перехода: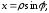
 полярная ось направлена вдоль оси Оу в
противоположную сторону. При подстановке
в уравнение получаем
полярная ось направлена вдоль оси Оу в
противоположную сторону. При подстановке
в уравнение получаем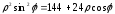 или
или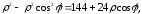 или
или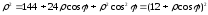 .
Решая это уравнение относительно
.
Решая это уравнение относительно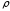 получим
получим каноническое уравнение параболы в
полярной системе координат.
каноническое уравнение параболы в
полярной системе координат.
93.5 Эллипс, вытянут вдоль оси
Оу.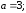
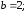
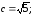
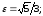
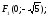
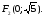 Формулы перехода:
Формулы перехода: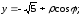
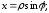 полярная ось направлена вдоль оси Оу
и совпадает по направлению. Полюс в
фокусе
полярная ось направлена вдоль оси Оу
и совпадает по направлению. Полюс в
фокусе . При подстановке в уравнение получаем
. При подстановке в уравнение получаем
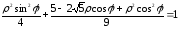 Приводим к общему знаменателю и
освобождаемся от
Приводим к общему знаменателю и
освобождаемся от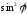 ,
получаем
,
получаем или
или .
Решая это уравнение относительно
.
Решая это уравнение относительно
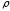 получим
получим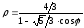 - каноническое уравнение эллипса в
полярной системе координат . 93.6
Гипербола.
- каноническое уравнение эллипса в
полярной системе координат . 93.6
Гипербола.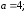
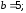
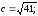
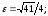
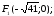
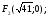 Формулы перехода:
Формулы перехода: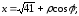
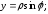 полярная ось направлена вдоль оси Ох
и совпадает с ней по направлению. При
подстановке в уравнение получаем:
полярная ось направлена вдоль оси Ох
и совпадает с ней по направлению. При
подстановке в уравнение получаем: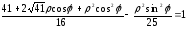 Приводим к общему знаменателю
и освобождаемся от
Приводим к общему знаменателю
и освобождаемся от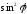 ,
получаем
,
получаем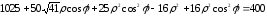 или
или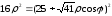 . Решая это уравнение относительно
. Решая это уравнение относительно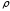 получим
получим
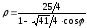 -каноническое уравнение гиперболы
в полярной системе координат.
-каноническое уравнение гиперболы
в полярной системе координат.
