
- •3.1.1.1. Определение числа степеней свободы масс
- •3.1.1.2. Расчётная схема рамы
- •3.1.1.3. Динамический расчёт по уравнениям в форме метода сил ( в амплитудах инерционных силовых факторов )
- •3.1.1.4. Динамический расчёт по уравнениям в форме
- •3.1.2. Расчёт рамы на статические нагрузки
- •3.1.3. Определение полных расчётных усилий
- •3.1.3. О приближённом учёте инерции вращения масс
- •Приложение к задаче 3.1
- •1 2 3 5 4 1 Перемещения узлов и узловые нагрузки Узел
- •Задача 3.2. Динамический расчёт симметричной системы
- •Задача 3.3. Динамический расчёт системы с взаимозависимыми перемещениями сосредоточенных масс
- •Задача 3.4. Приближённое определение частоты собственных колебаний
- •Задача 3.5. Расчёт системы с конечным числом степеней свободы масс на кинематические воздействия
- •3.5.2. Негармоническое кинематическое воздействие
- •Задача 3.6. Расчёт стержневой системы с гасителем колебаний на вибрационную нагрузку
- •4. Контрольные вопросы
3.1.1.1. Определение числа степеней свободы масс
2
3


п










 еремещения.
Пренебрегая
для стер-
еремещения.
Пренебрегая
для стер-
ж ней
рамы,
работающих
преимуще-
ней
рамы,
работающих
преимуще-
с










 твенно
на изгиб, сближениями их
твенно
на изгиб, сближениями их
к
1

м

 и
деформациями
и
искривлениями,
и
деформациями
и
искривлениями,
п

 олучаем
n
= 3 ( рис.
3.2 ).
олучаем
n
= 3 ( рис.
3.2 ).
Рис. 3.2
видно, что двумя степенями свободы
масс являются их линейные перемещения, а третья степень сво-боды – угол поворота неточечной массы.
3.1.1.2. Расчётная схема рамы
для решения кинетостатическим методом задачи о собственных колебаниях представлена на рис. 3.3, причём на рис. 3.3, а амп-литудные инерционные силовые факторы приложены к массам в их центрах тяжести, а на рис. 3.3, б – к раме с удалёнными мас-сами в местах прикрепления последних к узлам и элементам*) .
![]()
![]()
y3
y2
ur
=
y2 m
y2
Om
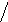



![]()
![]()
 а)
б)
а)
б)
J2(1)
J2(2)
em
=
lm
/2
m
/2
J2(r)





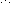












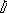

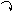










































J1
J1
J3






y1
y1 m





Рис. 3.3
 В расчёте на
гармонические
вынужденные колебания
в схему будут добавлены амплитуды
динамических воздействий.
В расчёте на
гармонические
вынужденные колебания
в схему будут добавлены амплитуды
динамических воздействий.
*) В этом случае их следует понимать ( см. с. 17 – 20 ) как реакции линейных и угловых связей, прикрепляющих массы к безынерционной (безмассовой) деформируемой системе, выраженные через инерционные силы и моменты. С учётом этого в дальнейшем на большинстве схем массы не изображаются.
Последовательно рассмотрим оба представленных в главе 1 возможных варианта решения – по основным уравнениям гар-монических (собственных или вынужденных) колебаний, в кото-рых за основные неизвестные принимаются либо амплитуды инерционных силовых факторов, либо амплитуды динамических перемещений масс ( см. п. 1.5.4 и 1.5.5 ).
3.1.1.3. Динамический расчёт по уравнениям в форме метода сил ( в амплитудах инерционных силовых факторов )
По любой из
схем
рис. 3.3 общее число инерционных сил и
моментов
равно
4.
Но
количество
основных
неизвестных должно совпадать с числом
степеней свободы масс,
т.е. 3. Кажущееся несоответствие
устраняется, если учесть, что не все
компоненты перемещений масс являются
независимыми: точки прикрепле-ния к
раме двух масс, расположенных по концам
верхнего риге-ля рамы, имеют одинаковые
горизонтальные перемещения ur
=
y2
(
см.
рис.
3.3,
б
).
Вследствие
этого силы
J2(1)
и J2(2)
,
порождаемые
общим
перемещением
y2
,
–
взаимозависимые,
пропорциональ-ные
массам; их
отношение J2(1)
:
J2(2)
=
m
:
(m/2)
=
2. В качестве
одного из трёх
основных неизвестных можно принять
любую из сил J2(1)
или J2(2)
либо, что
удобнее, их
сумму:
J2
= J2(1)
+ J2(2)
.
Два остальных
– вертикальная
сила
инерции
J1
и
инерционный
мо-мент
J3
.
Силе
J1
, независимой
от J2
и J3
, соответствуют
порож-дающие её масса m1
= m
и перемещение y1
. Инерционные
фак-торы J2(1)
и J3
, связанные
с линейным y2
и угловым y3
пере-мещениями
неточечной массы m,
эксцентрично
прикреплённой к узлу рамы, следует
рассматривать как обобщённые
(
групппо-вые
).
Для
определения
отвечающих им
приведённых
масс
![]() используем
методику и
формулы, представленные
в
п.
1.6. Сопоставляя
рис. 3.3,
б с
рис. 1.43,
оцениваем
J2(1)
и J3
в данной
задаче
как
аналоги
используем
методику и
формулы, представленные
в
п.
1.6. Сопоставляя
рис. 3.3,
б с
рис. 1.43,
оцениваем
J2(1)
и J3
в данной
задаче
как
аналоги
![]() и
и
![]() ,
тогда по формуле (
1.135
):
,
тогда по формуле (
1.135
):
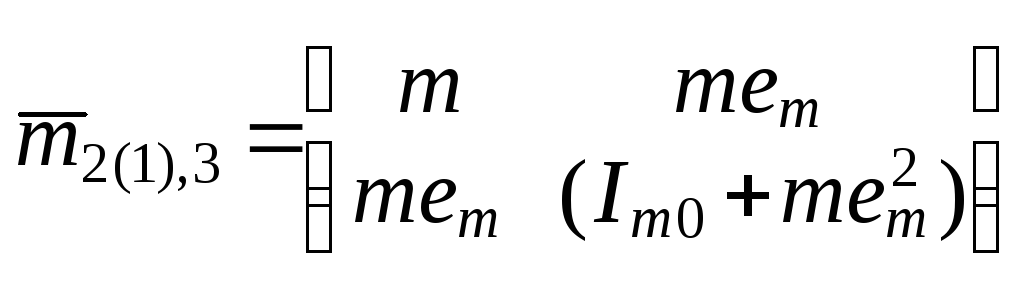 .
.

![]()
и
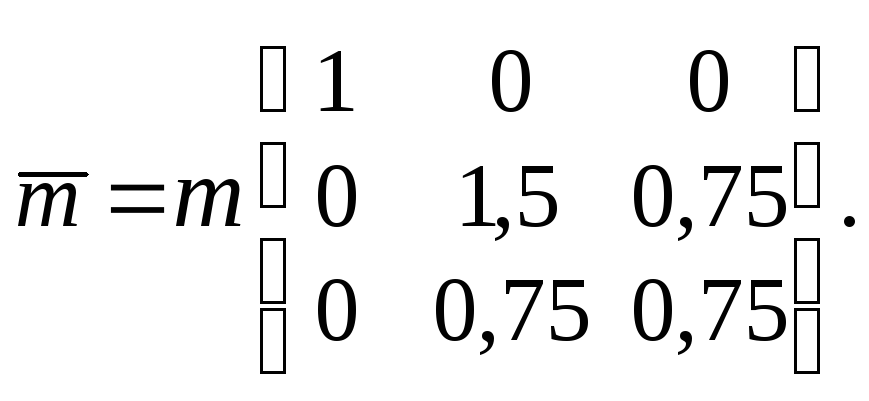
![]() /12
= = (0,1875 м2)
m:
/12
= = (0,1875 м2)
m:
Р а с ч ё т н а с о б с т в е н н ы е к о л е б а н и я
А. Уравнения собственных колебаний
в амплитудах инерционных силовых факторов
В соответствии с расчётной схемой рис. 3.3, б система уравне-ний ( 1.51 ) записывается как
 (
3.1
)
(
3.1
)
Если принять
в качестве параметра массы m0
= m,
то матри-ца, входящая в вычитаемое в
скобках развёрнутого выражения матрицы
динамической
податливости![]() ,
принимает
смысл
матри-цы
a
относительных масс (см. с. 54). Выполняем
её обращение:
,
принимает
смысл
матри-цы
a
относительных масс (см. с. 54). Выполняем
её обращение:

Введём параметр
0
=
1/(m0
2),
после чего систему уравне-ний представим
в виде
![]() :
:
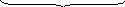
 (
3.2
)
(
3.2
)
J
![]()
Для определения
единичных перемещений ik
(![]() ),
являющихся компонентами матрицы
упругой
податливости
),
являющихся компонентами матрицы
упругой
податливости
рассчитываемой системы по направлениям основных неизвест-ных J, далее потребуется рассмотреть единичные состояния заданной рамы от действия Jk = 1 ( k = 1, 2, 3 ).
Б. Формирование матрицы упругой податливости системы
Компоненты матрицы определяются методом Максвелла – Мора по любому из равносильных вариантов формулы этого метода для перемещений в статически неопределимых системах от силовых воздействий ( в рамах – с учётом только деформаций изгиба элементов ):
![]() (
3.3
)
(
3.3
)
где Mi , Mk – изгибающие моменты в заданной статически неоп-
ределимой системе от единичных основных неиз-
вестных Ji = 1 и Jk = 1 cоответственно;
![]() –
изгибающие
моменты
от
Ji
=
1
и
Jk
=
1 в любой
вспо-
–
изгибающие
моменты
от
Ji
=
1
и
Jk
=
1 в любой
вспо-
могательной статически определимой системе, по-
лученной из заданной СНС удалением лишних свя-
зей.
В любом случае необходимо рассмотреть три единичных состояния заданной рамы ( рис. 3.4, а, б, в ). Расчёт рамы, степень статической неопределимости которой nst = 3, степень кинемати-ческой неопределимости nk = 3, на единичные воздействия J1 = 1, J2 = 1 и J3 = 1 выполняется рациональным методом ( сил, переме-щений, смешанным или конечных элементов ), «вручную» или с использованием компьютерных программ. Поскольку эта часть динамического расчёта играет в решаемой задаче «служебную» роль и сводится к использованию знаний из предыдущего курса строительной механики, то подробное изложение этого этапа вынесено в Приложение к задаче 3.1 (см. с. 163), а на рис. 3.5 представлены сразу его результаты в виде единичных эпюр изги-бающих моментов.
Замечание к рис. 3.4, б: любую из сил J2(1) = 2/3 или J2(2) = 1/3 можно перенести по линии действия в точку приложения другой и просуммиро-вать с ней, получая в результате J2 = 1 в соответствующей точке (на ле-вом или правом конце верхнего ригеля рамы). Это не изменит изгибаю-щие моменты М2; неправильно будут описаны только продольные силы в ригеле, но они не учитываются на этом этапе расчёта.
21
31
0,0608
0,4257
0,6993



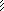
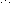





























11
0,2128






k =
1
k =
3
M3
M1





J1
=
1
1,1502
22
J2(1)
=
2/3
J2(2)
=
1/3
0,8649


























32
1,8378





12
2,1622






k =
2
0,4324
0,8649
M2

23
33
J3
=
1


0,1351






















0,8649
0,0540







13


0,0540
0,0270





Рис. 3.4
4
J3
=
1
J2
=
1
J1
=
1











1
4


 а) б)
в) г)
а) б)
в) г)
1,5










![]()
![]()
![]()
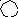






Рис. 3.5
Все
эпюры
изгибающих
моментов
![]() в
этой
системе –
достаточно простые и компактные, поэтому
нет необходимости использовать другие
вспомогательные СОС для упрощения
единичных эпюр.
в
этой
системе –
достаточно простые и компактные, поэтому
нет необходимости использовать другие
вспомогательные СОС для упрощения
единичных эпюр.
Используя для определения каждого из перемещений ik наиболее выигрышный по трудоёмкости вариант, находим:
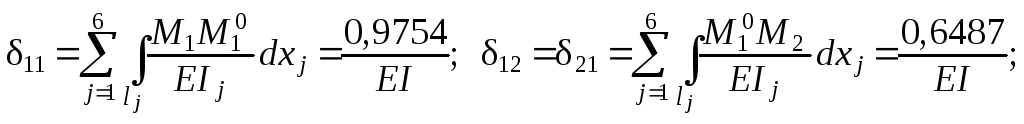

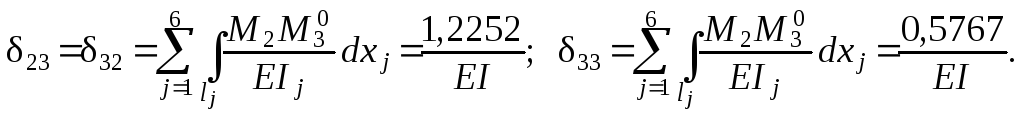
Заметим, что
можно было бы обойтись и без дополнитель-ных
эпюр
![]() ,
вычисляя ik
по
первой
из
формул (
3.3
)
через моменты
Mk
в
заданной
СНС
(
по рис.
3.4, г –
е
).
Этот
вариант
,
вычисляя ik
по
первой
из
формул (
3.3
)
через моменты
Mk
в
заданной
СНС
(
по рис.
3.4, г –
е
).
Этот
вариант
рационален в случае компьютерного расчёта ( см. Приложение к задаче 3.1 ).
В. Уравнение частот собственных колебаний
получается из
нетривиального
решения
J![]() системы
уравнений (
3.2
), т.е. из
условия
существования
движения, и
имеет вид
системы
уравнений (
3.2
), т.е. из
условия
существования
движения, и
имеет вид
![]() .
(
3.4
)
.
(
3.4
)
Компоненты матрицы упругой податливости содержат характеристику изгибной жёсткости EI: ik = dik /EI ( здесь dik – числитель выражения ik ). Её целесообразно включить в собст-венное число: = EI /(m02) = EI0 ( заметим, что размерность – [длина]3). Подстановка0 =/EI в ( 3.4 ) даёт частотное уравнение
 (
3.5
)
(
3.5
)
позволяющее найти величины j ( j = 1, 2, 3 ) с помощью стан-дартных процедур решения задачи линейной алгебры о собствен-ных значениях матричного линейного оператора. Существуют реализующие их компьютерные программы, в частности, такие, как LOVEK и DINAM, разработанные на кафедре строительной механики НГАСУ (Сибстрин). В программе LOVEK задача пред-
ставлена в виде
![]() При EI
При EI
![]() 0
из ( 3.5
) получаем
0
из ( 3.5
) получаем

Введя в компьютер матрицы А и В, в результате расчёта по программе LOVEK получаем запись характеристического ( в рас-сматриваемой задаче – частотного ) уравнения, его корни ( собст-венные значения 1, 2 и 3 ) и соответствующие им собственные векторы J (j) основных неизвестных ( инерционных силовых фак-
т оров
):
оров
):
1,7778 3 + 29,6024 2 – 29,6412 + 3,3700 = 0;


 1 =
15,5892; 2
= 0,93111;
3
= 0,13059;
1 =
15,5892; 2
= 0,93111;
3
= 0,13059;
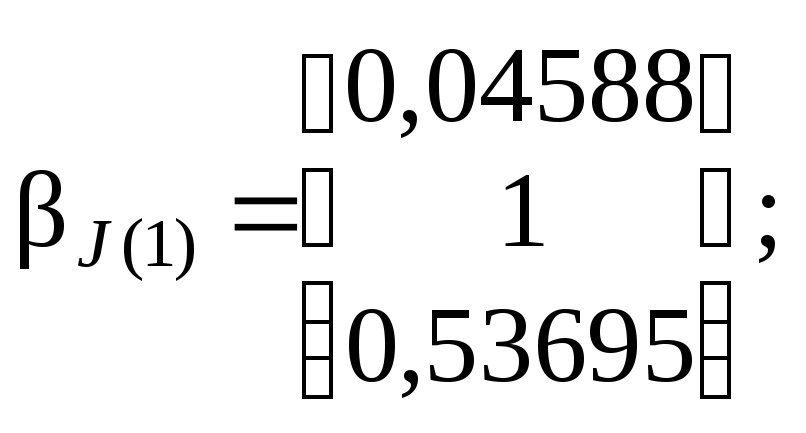
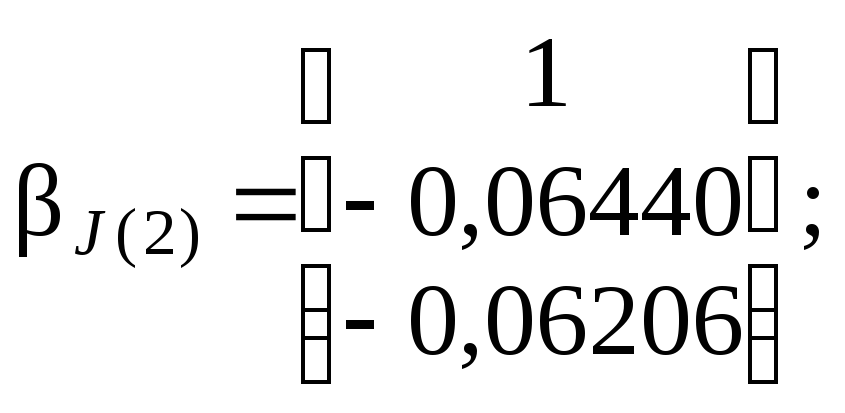
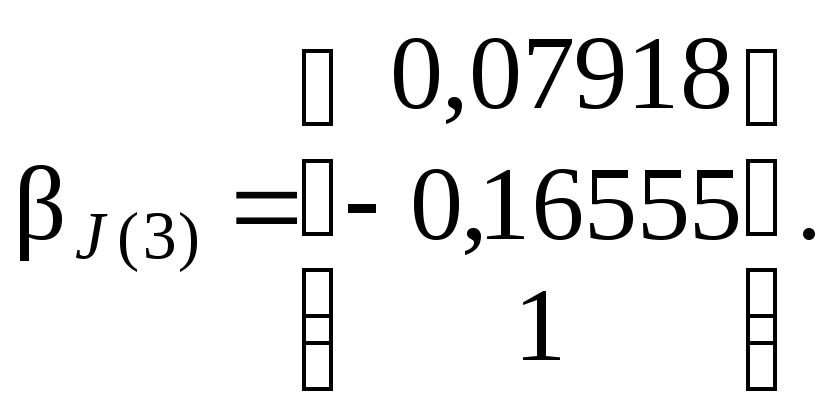
Если
не учитывать инерцию вращения неточечной
массы, т.е. принять lm
= 0, то число степеней свободы
уменьшается
на
1
(
n
=
2
),
из расчётной схемы (рис. 3.3) ис-ключается
инерционный
момент
J3,
число уравнений сокращается до двух,
и частотное уравнение принимает вид
1 =
13,455
м3;
2
=
0,92482
м3.
Им
соответствуют собственные векторы
J(1)
=
[ 0,05198
1 ]т
и
J(2)
=
[
1
–
0,07796
]т
.
Эти
результаты отличаются от полученных
при n
=
3
–
объясне-ние
дано в п. 1.5.4.3.
![]() Корни
этого уравнения:
Корни
этого уравнения:
венных колебаний
![]() :
:
![]() =
=
![]()
= 35,818 c –1 ;
![]() =
=
![]()
= 146,56 c –1 ;
![]() =
=
![]()
= 391,35 c –1 ;
технические частоты fj = j /(2):
f1 = 1 /(2) = 5,70 Гц; f2 = 2 /(2) = 23,33 Гц; f3 = 3 /(2) = 62,29 Гц.
Г. Определение собственных векторов перемещений,
построение главных форм колебаний и проверка их ортогональности
Главные формы колебаний характеризуются собственными векторами перемещений масс y (j) , которые вычисляются через найденные выше соответствующие векторы J(j) по соотноше-нию ( 1.58 ):

аналогично
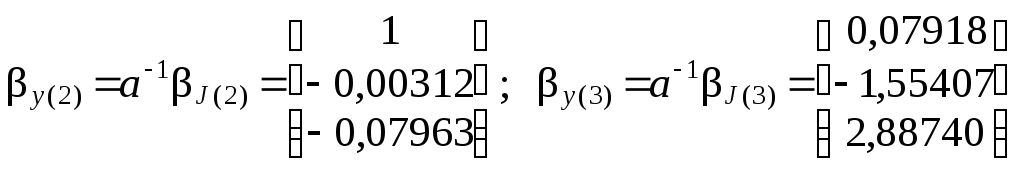 .
.
Компоненты каждого вектора для удобства делим на наи-больший из них по абсолютной величине:
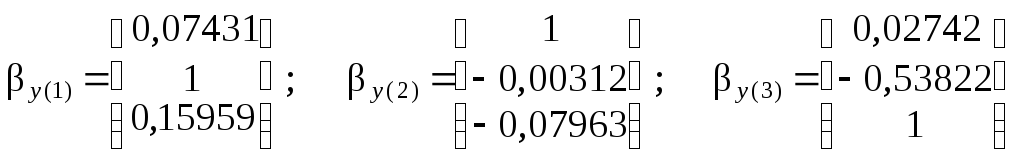 .
.
С помощью векторов y (j) ( j = 1, 2, 3 ) строим схемы главных форм собственных колебаний ( рис. 3.6, а – в ), учитывая, что компоненты y3 (1) и y3 (2) не безразмерные – они измеряются в м –1
из-за того, что у3 – угловое перемещение, а у1 и у2 – линейные. По той же причине y1 (3) и y2 (3) измеряются в метрах. Обратные величинам y3 (1) и y3 (2) отрезки by3 (1) = 1/y3 (1) = 6,27 м и by3 (2) = = 1/ |y3 (2)| = 12,56 м, а также y1 (3) и y2 (3) в графических построе-ниях на рис. 3.6 изображаются в том же масштабе, что и сама рама. Уточнению схем деформаций в главных формах могут способствовать эпюры изгибающих моментов ( рис. 3.6, г – е ), вычисленных на основании формулы ( 1.64 ):
![]()
Выполняем проверку ортогональности главных форм, ис-пользуя разные варианты условий ( 1.60 ):
![]()
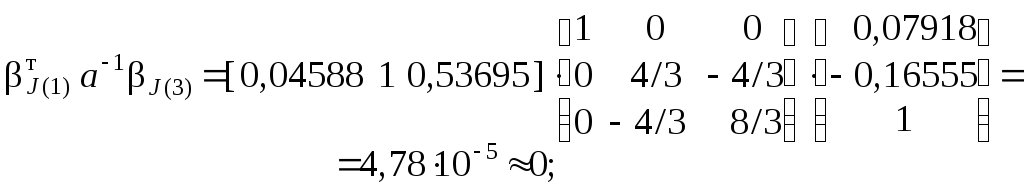
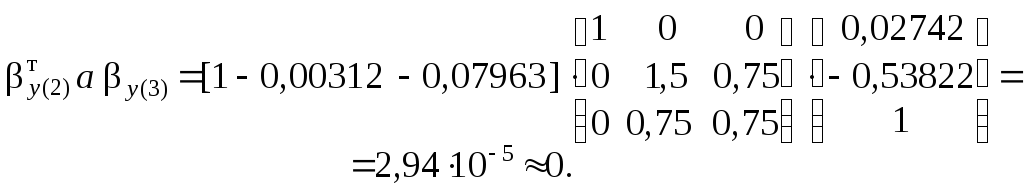
y3(1)
=
y2(1)
y3(1)
=
=
y2(1)
/
by3(1)
1,7681

y2(1)

 а) г)
а) г)
0,9134


























y1(1)
=
y2(1)
y1(1)
2,3051




2,2318








j =
1
(1)
0,4567
=
y3(1)
0,4998



![]()

0,8618



y3(2)
=
y1(2)
y3(2)
=
=
y1(2)
/
by3(2)
0,1113

0,0492
j =
2
(2)




0,7584
y2(2)
=
=
y1(2)
y2(2)



















 д)
д)
0,3666
0,2084





0,1834
y1(2)












k =
3
M 3
2
=
|
y3(2)|




![]()

1,1206
by3(2)
=
12,56
м
y3(3)


y2(3)
=
y3(3)
y2(3)
0,4344
y2(3)


























 е)
е)
0,5656
0,1446
y1(3)
=
y3(3)
y1(3)










0,2278
0,0555
j =
3
(3)
0,0465![]()










0,0278
Рис. 3.6
Д. Статическая и кинематическая проверки
0,5370
1/3




м
2/3

 ы
колебаний схема для
провер-
ы
колебаний схема для
провер-
к
0,0459
0,1522
0,3842 и
условного равновесия рамы
в
и
условного равновесия рамы
в
ц
O

п
1,1142


 риведена
на рис.
3.7. В качестве
риведена
на рис.
3.7. В качестве
и
0,1666
к
0,1142
0,3526
с
y


J2(1)
=
2/3
6
м
3
3 и
J2(2)
= 1/3
( см. с.
137).
и
J2(2)
= 1/3
( см. с.
137).
x



н
Рис. 3.7
найдены по
эпюре
![]() ,
а
про-
,
а
про-
дольные силы – из условий равновесия узлов и элементов рамы.
Выполняем статическую проверку:
x = –1,1142 + 2/3 + 1/3 + 0,1142 = 0 ;
y
= –0,1522
–
0,3526
–
0,0459
+
0,1666
+
0,3842
=
0,0001![]() 0;
0;
mO
=![]()
![]()
Дополнительно можно контролировать выполнение усло-вий равновесия по Д’Аламберу для отсечённых частей рамы.
Аналогично производится статическая проверка и для дру-гих главных форм.
Кинематическая проверка
осуществляется по формуле ( 1.63 ), преобразованной с учётом того, что 0 =/C0 , к следующему виду:
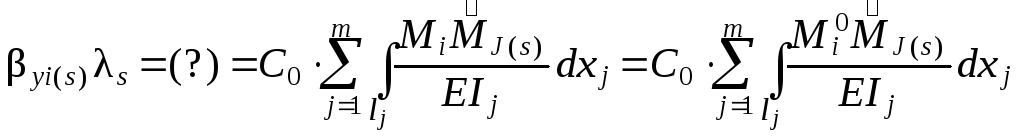 (
3.6
)
(
3.6
)
(
здесь s
– номер главной формы
). Особо
отметим, что
величи-на yi(s)
берётся из собственного вектора
перемещений, получен-ного
непосредственно
из
выражения
![]() ,
без
деления
на его наибольший компонент
(
выше
этот приём
использован для удобства построения
главных форм
).
,
без
деления
на его наибольший компонент
(
выше
этот приём
использован для удобства построения
главных форм
).
Для
i
=
2,
s
=
1
(
проверка
перемещения y2
в первой
главной форме): y2(1)
1
=
0,6174![]() =
9,6248; учтём,
что
С0
=
EI,
тогда
=
9,6248; учтём,
что
С0
=
EI,
тогда
правая часть проверяемого равенства ( 3.6 ) будет
 расхождение
в
четвёртой
значащей
цифре
(
погрешность
0,005
%).
расхождение
в
четвёртой
значащей
цифре
(
погрешность
0,005
%).
Таким же образом проверяются и все остальные перемеще-ния.
Расчёт на установившиеся вынужденные колебания
Согласно условию задачи, частоту вибрационной нагрузки с компонентами F(t) и q(t) вычисляем через найденную мини-мальную частоту собственных колебаний min = 1 = 35,818 с –1 :
соответствующая
характеристика F
=![]() =
=![]() =
=![]() = 32,236
с –1
;
= 32,236
с –1
;
= 19,246
м3.
А
F
lm
y3
п
J3
J2
/3
F
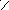


![]()
к
 а
F
приведена к узлу.
а
F
приведена к узлу.
y2
q























г

 армонических
вынужденных
ко-
армонических
вынужденных
ко-
л










 ебаний
в амплитудах инерцион-
ебаний
в амплитудах инерцион-
н
y1
J1

 ых
силовых факторов:
ых
силовых факторов:
![]() =
=
Рис. 3.8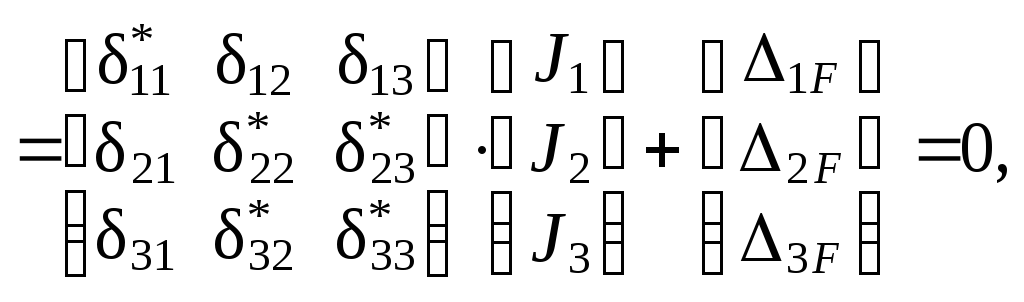
![]()
Б. Формирование матрицы * динамической податливости системы
Вычисляем матрицу динамической податливости *, ис-пользуя полученную ранее матрицу упругой податливости :


Б. Определение перемещений F
8,9189
F
lm
=
4,5![]()
4,4189
F
=
3
кН
3F
8,4325








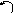









q
=
2
кН/м
2F
7,5811
0,5676























1F
0,2838







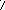
F
MF
4,6419
0,4257![]()


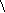

4,7838
Рис. 3.9
Вызванные этим воздействием изгибающие моменты MF , эпюра которых дана на рис. 3.8, б *), используем в расчёте пере-мещений по формуле Максвелла – Мора:
![]()
где Mi
и
![]() –
то же, что в формуле (
3.3
).
–
то же, что в формуле (
3.3
).
Очевидно,
что
предпочтителен
второй
вариант
(
с
![]() и
MF
).
Вариант
с
моментами
и
MF
).
Вариант
с
моментами![]() не
актуален,
так
как
без
определения
MF
не
актуален,
так
как
без
определения
MF
обойтись невозможно – они необходимы для вычисления динами-ческих моментов.

*) Расчёт на амплитудные значения динамических нагрузок приведён
в Приложении к задаче 3.1.
«Перемножением»
эпюры MF
c
эпюрами
![]() по
рис.3.5 на-ходим:
по
рис.3.5 на-ходим:
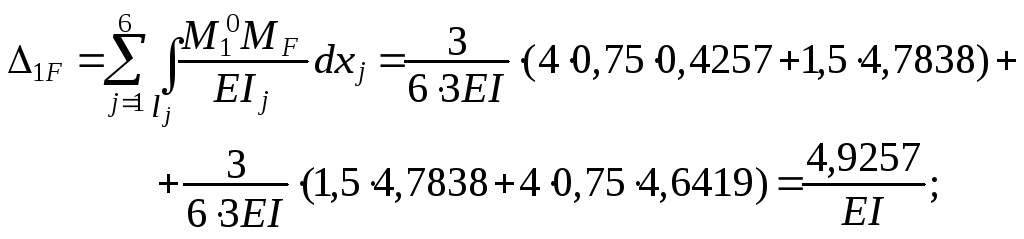


В. Определение основных неизвестных и динамических усилий
Система уравнений для определения амплитуд инерцион-ных силовых факторов при вычисленных * и F :

37,201
Mdyn
![]()
 Решение её
с помощью
программы LINS
даёт J1
= –0,181
кН; J2
= –12,269
кН ;
J3
= –6,618
кН
Решение её
с помощью
программы LINS
даёт J1
= –0,181
кН; J2
= –12,269
кН ;
J3
= –6,618
кН![]() .
.
С удя
по знакам, все три инерци-
удя
по знакам, все три инерци-
о
26,084
л
19,275






н
0,909
7,842 ым
на рис. 3.8.
ым
на рис. 3.8.

 Используя
найденные J1
,
J2
Используя
найденные J1
,
J2
и
10,478
1,796



н
34,992
5,239
Qdyn
Ndyn
![]()

![]()
 Mdyn
= M1
J1
+ M2
J2
+ M3
J3
+ MF
.
Mdyn
= M1
J1
+ M2
J2
+ M3
J3
+ MF
.
6,200


4,090










15,269
1,746
9,122
6,200







2,697








13,576


1,310
16,579
Рис. 3.10

По Mdyn обычными приёмами определяем соответствующие
им амплитуды поперечных и продольных сил Qdyn и Ndyn .
На рис. 3.10 приведены эпюры Mdyn , Qdyn и Ndyn ( сплошны-ми линиями – для направлений амплитудных нагрузок, принятых по схеме рис. 3.9, а, пунктиром – в противоположной фазе ).
Г. Проверки результатов расчёта на вынужденные колебания
Статическая проверка –
в
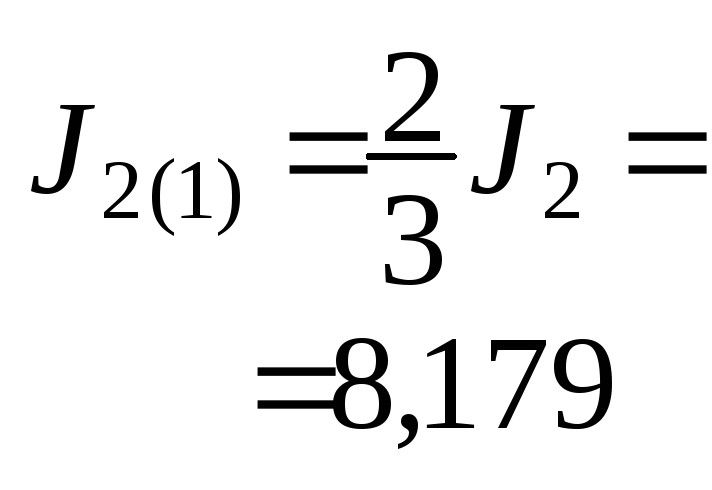
J3
=
6,618
.
37,201
dy dx



F
=
3
4,090

dy
Flm
=
4,5
6,200


15,269



6,200
26,084 y
1,746
2,697
6,200
q
=
2
34,992 K











16,579
15,269


x 3 3













J1
=
0,181

1,310
6
м
13,576
Рис. 3.12
Можно также проверять равновесие других узлов, отсечён-ных частей и рамы в целом.
Кинематическая проверка –
контроль амплитуд перемещений масс – выполняется по форму-ле ( 1.87 ) с изменением левой части с учётом зависимости ( 1.121 ):
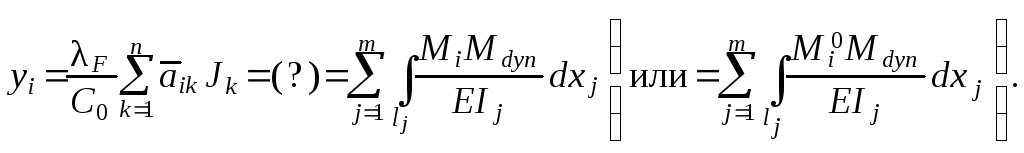
расхож-
дение
0,17
%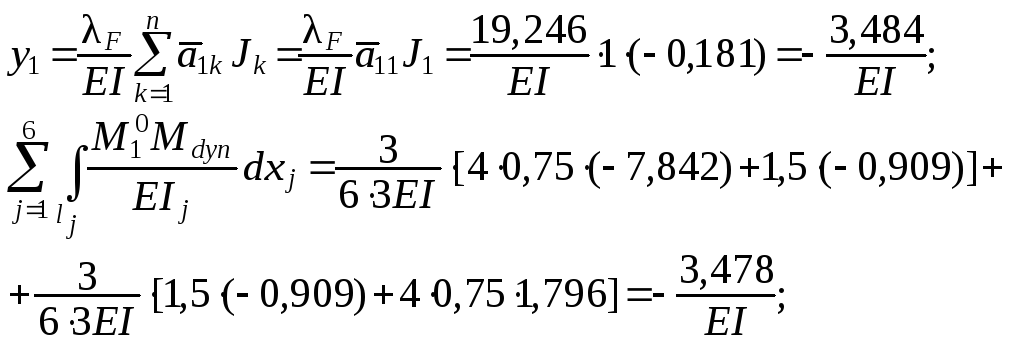

расхожде-
ние 0,005
%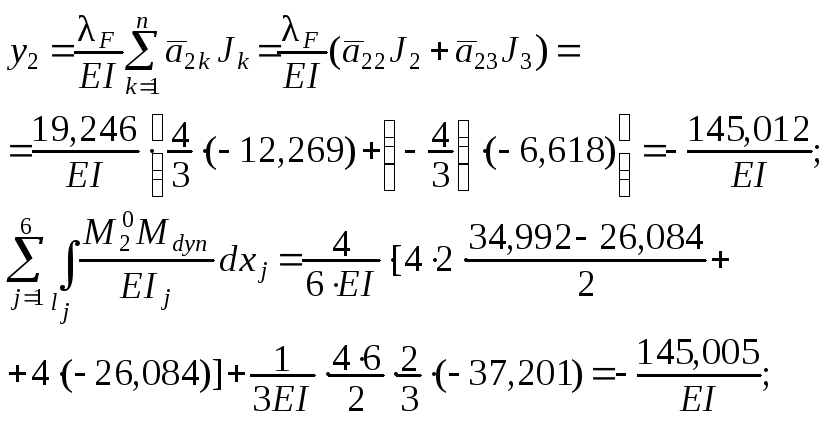
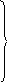
расхожде-
ние 0,06
%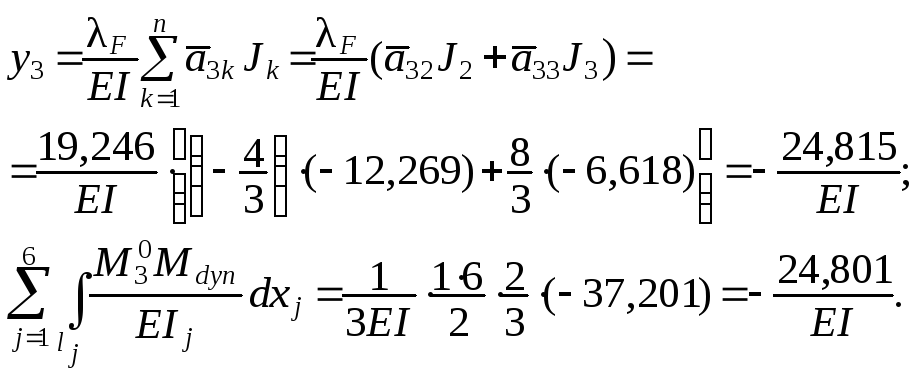
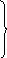
Г. Вычисление динамических коэффициентов
а) по наибольшему из компонентов перемещений масс
Наибольшее по абсолютной величине динамическое пере-мещение – у2 = – 145,04/EI ( найдено выше в кинематической про-верке ); соответствующее статическое значение ( от амплитуды динамической нагрузки ) – 2F = –27,13/EI , тогда
y2 = y2 /2F = 145,01/27,13 = 5,345;
б) по наибольшему ( по абсолютной величине )
изгибающему моменту в раме
По эпюре Mdyn
находим, что |
Mdyn
|
max
= 37,201
![]() – в ле-вом концевом сечении верхнего
ригеля;
статическое
значение (
с эпюры MF
) –
|
MF
|
= 8,919
– в ле-вом концевом сечении верхнего
ригеля;
статическое
значение (
с эпюры MF
) –
|
MF
|
= 8,919
![]() ;
;
Mmax = | Mdyn | max / | MF | = 37,201/8,919 = 4,171.
Для сравнения: в нижнем сечении стойки верхнего яруса рамы: Mс = Mdyn, c / MF, c = 34,992 / 7,581 = 4,616.
