
- •3.1.1.1. Определение числа степеней свободы масс
- •3.1.1.2. Расчётная схема рамы
- •3.1.1.3. Динамический расчёт по уравнениям в форме метода сил ( в амплитудах инерционных силовых факторов )
- •3.1.1.4. Динамический расчёт по уравнениям в форме
- •3.1.2. Расчёт рамы на статические нагрузки
- •3.1.3. Определение полных расчётных усилий
- •3.1.3. О приближённом учёте инерции вращения масс
- •Приложение к задаче 3.1
- •1 2 3 5 4 1 Перемещения узлов и узловые нагрузки Узел
- •Задача 3.2. Динамический расчёт симметричной системы
- •Задача 3.3. Динамический расчёт системы с взаимозависимыми перемещениями сосредоточенных масс
- •Задача 3.4. Приближённое определение частоты собственных колебаний
- •Задача 3.5. Расчёт системы с конечным числом степеней свободы масс на кинематические воздействия
- •3.5.2. Негармоническое кинематическое воздействие
- •Задача 3.6. Расчёт стержневой системы с гасителем колебаний на вибрационную нагрузку
- •4. Контрольные вопросы
3.1.3. О приближённом учёте инерции вращения масс
В дополнение к решению основной задачи рассмотрим во-прос приближённого учёта инерции вращения сосредоточенной неточечной массы.
m/2
о
J2(1)
lm
m/2
J2(2)

![]()

m/2
J1





 Матрица приведённых масс
а)
Матрица приведённых масс
а)
![]()







 =
m
m
m/2
,
тогда
при
=
=
m
m
m/2
,
тогда
при
=
= m










 EI
/(m2)
получается
EI
/(m2)
получается
![]() =
1 1
2 .
=
1 1
2 .
![]() =
1
=
1![]()
я



 ния
и эпюры М1
и М2
остаются та-
ния
и эпюры М1
и М2
остаются та-
к

 ими
же, как в выполненном выше
ими
же, как в выполненном выше
р
Рис. 3.19
вующем
![]() =
1
(рис.
3.19,
б), момен-
=
1
(рис.
3.19,
б), момен-
ты
![]() =
М2
+
М3
=
М2
+
М3![]() (
здесь М2
и М3
– по рис.3.4
), тогда
компонен-ты
матрицы
упругой
податливости
с
учётом
изменения
смысла
(
здесь М2
и М3
– по рис.3.4
), тогда
компонен-ты
матрицы
упругой
податливости
с
учётом
изменения
смысла
![]() будут:
будут:
![]()
![]() ,
где
ik
(
i,
k
=
1,
2,
3)
–
из
основного
расчёта.
,
где
ik
(
i,
k
=
1,
2,
3)
–
из
основного
расчёта.
Решив для
определения частот собственных колебаний
за-дачу Det
(![]() )
=
0,
)
=
0,
где
 ;
;
 ,
,
п
Обратим
внимание
на
то,
что
игнорирование
инерции
вращения
неточеч-ной
массы для рассматриваемой системы
приводит к существенной
ошибке
в определении
минимальной
частоты собственных колебаний
–
7,7
%
(
см.
с.
139
).
Приложение к задаче 3.1
Рассматриваются вопросы, относящиеся к технике вычис-ления силовых факторов в заданной статически неопределимой системе от единичных основных неизвестных динамического расчёта ( амплитуд инерционных силовых факторов ) и всех за-данных нагрузок.
Z2

















н
X1
л енной
на рис. 3.20.
енной
на рис. 3.20.



 Канонические
уравнения:
Канонические
уравнения:



Рис. 3.20
свободных членах уравнений указы-
вает на то, что соответствующие величины определяются в ос-новной системе и от иных, чем в динамическом расчёте, единич-ных воздействий – основных неизвестных X1 = 1 и Z2 = 1.
Рама рассчитывается на следующие варианты силовых воз-действий:
– единичные инерционные силовые факторы J1 = 1, J2 = 1, J3 = 1 ( отдельно ), рассматриваемые здесь формально как нагрузки;
– одновременно действующие амплитудные динамические на-грузки F и q, далее обозначаемые символом Fd ;
– постоянная нагрузка от весов масс ( G );
– снеговые нагрузки р(1) и р(2) – отдельно на двух участках.
 Соответственно
индекс F
в свободных членах 0,1F
и R0,2F
канонических уравнений в разных вариантах
истолковывается как
F
Соответственно
индекс F
в свободных членах 0,1F
и R0,2F
канонических уравнений в разных вариантах
истолковывается как
F
![]() (
J1
J1
J1
Fd
G
р(1)
р(2)
).
(
J1
J1
J1
Fd
G
р(1)
р(2)
).
2
=
0
0,11
=
1
+
1
![]() =
–2
=
–2
![]() ,
,![]() и r0,22
рас-сматриваем единичные состояния
ОССМ ( рис.
3.21 ).
и r0,22
рас-сматриваем единичные состояния
ОССМ ( рис.
3.21 ).
Z2
=
1
X1
=
1

1
3EI































































![]()
2
(<0)
1
r0,22
EI







3EI
3EI




EI



l
=
6
м
l

1







![]()



![]()
![]()

1


1



![]()
Рис. 3.21
Вычислив
«перемножением» эпюр
способом вырезания
узла – r0,22
=
3,75EI,
![]() =
1 и по теореме
Рэлея
=
1 и по теореме
Рэлея
![]() ,
затем аналогично определяем свободные
члены канонических
уравнений
для
вышеперечисленных
вариан-
,
затем аналогично определяем свободные
члены канонических
уравнений
для
вышеперечисленных
вариан-
т
0,1J1
J2(1)
=
2/3
J2(2)
=
1/3
J3
=
1
R0,2J1
R0,2J2

J1
=
1
0,1J2
0,1J2






































































R0,2J3
=
0
























1
1,125 4

0,9375
![]()

![]()

![]()

Рис. 3.22
p(2)
=
8
кН
/м
0,1p(1)
=
0
Flm
=
4,5
кНм
F
=
3
кН
R0,
2p(1)
R0,
2
p(2)
=
0













R0,
2F
0,
1p(2)

































































p(1)
=
8
кН
/м
























q
=
2
кН
/м



4,5
36









9 36 12



18
![]()

![]()

![]()

(![]() )
(
)
(![]() )
(
)
(![]() )
)
Рис. 3.23
Матрица
перемещений
0,
1F
= и реакций
R0,
2F
по шести вариантам нагрузок:
и реакций
R0,
2F
по шести вариантам нагрузок:
 .
.
Основные неизвестные:
 По найденным
значениям Х1
и Z2
вычисляем изгибающие моменты
По найденным
значениям Х1
и Z2
вычисляем изгибающие моменты
![]() .
.
По
вариантам F
![]() (
J1
J2
J3
) эпюры M1
, M2
и M3
приведены на
рис.
3.4,
от
амплитудных
динамических
нагрузок
–
на
рис.
3.10,
(
J1
J2
J3
) эпюры M1
, M2
и M3
приведены на
рис.
3.4,
от
амплитудных
динамических
нагрузок
–
на
рис.
3.10,
от временных нагрузок р(1) и р(2) – на рис. 3.17.
Далее рассмотрим применение двух других классических методов – сил и перемещений – для решения той же задачи опре-деления усилий в заданной СНС, с использованием матричной формы расчёта и соответствующих компьютерных программ.
b5
c5
e5
e4



5

























X1
X3
b4 1 4


 а) б)
а) б)
b2
c2
e2
b3
c3
e3




X2
b1
c1
e1



























b6 2 3 6






e6
Р


 ис.
3.24
ис.
3.24
Схема расчётных участков и сечений дана на рис. 3.24, б. При её формировании учтены границы грузовых участков и ха-рактер воздействий во всех единичных и «грузовых» состояни-ях, представленных на рис. 3.25 ( от единичных основных неиз-вестных метода сил Xk = 1, k = 1, 2, 3 ) и на рис. 3.26 ( от амплитуд динамических нагрузок и от снеговых нагрузок*) ). Эпюры M0, k от
Jk
=
1
(
k
= 1,
2,
3
)
–
такие
же,
как
![]() на
рис. 3.5.
на
рис. 3.5.


























X1
=
1
X2
=
1
X3
=
1

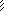


































![]() =
1
=
1
![]() =
2
=
2
![]() =
3
=
3
1

1






1
1
1
1




1
![]()

![]()

![]()
Рис. 3.25
* )
Об учёте
весов масс объяснения даны на с. 158.
)
Об учёте
весов масс объяснения даны на с. 158.
F
=
3
кН
Flm
=
4,5
кНм
p(1)
=
8
кН
/м
p(2)
=
8
кН
/м


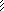




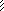









































































q
=
2
кН
/м
Fd
p(1)
p(1)



16,5
36
12

![]()




![]()






9



![]()


36
(![]() )
(
)
(![]() )
(
)
(![]() )
)
Рис.3.26
Единичные инерционные воздействия, динамические и ста-тические нагрузки рассматриваются как шесть вариантов загру-жения рамы, усилия от которых включаются в матрицу LF ис-ходных данных для расчёта рамы по программе MEFOR, разрабо-танной в НГАСУ ( Сибстрин ). В матрицу L входят усилия ( мо-менты ) от единичных основных неизвестных Xk = 1 ( k = 1, 2, 3 ).
1 2 3 5 6
4![]()
![]()




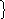








Остальные данные для ввода в компьютер:
– длины расчётных участков: l1 = l5 = 6 м; l2 = l3 = 3 м; l4 = l6 = 3 м;
– относительные жёсткости сечений участков cj = EIj /EI:
c1 = c2 =c3 = c5 = 3; c4 = c6 = 1.
Результаты расчёта:
усилия в заданной системе по вариантам загружений
от J1 = 1 J2 = 1 J3 = 1 F, q p(1) p(2)

![]()
По первым трём столбцам матрицы S строятся эпюры М1 , М2 и М3 ( рис. 3.4 ), а остальные дают соответственно MF ( рис. 3.10 ), Mр(1) и Mр(2) ( рис. 3.17 ). Моменты MG от сил тяжести
масс определяются через единичные М1 ( см. с. 159 ). Найденные М1 , М2 , М3 и MF далее можно использовать в динамическом рас-чёте для вычисления единичных перемещений – компонентов матрицы упругой податливости , а также перемещений F от амплитуд динамических нагрузок. Но эти величины могут быть найдены и с помощью программы MEFOR – для этого следует в дополнение к исходным матрицам L и LF ввести матрицу уси-лий от единичных воздействий по направлениям искомых пере-мещений, т.е. от J1 = 1, J2 = 1 и J3 = 1 – эта матрица совпадает с первыми тремя столбцами LF . В результате расчёта кроме усилий S выдается также матрица перемещений в заданной системе по направлениям J1 , J2 и J3 по вариантам загружений:

Первые три столбца – матрица упругой податливости , четвёртый – вектор свободных членов F уравнений *J + F = 0. Эти перемещения используются в динамическом расчёте. Они полностью совпадают с найденными в основном решении «пере-множением» соответствующих эпюр ( см. с. 138 и 145 ).
Z1 1
Z3 Погонные изгибные
Погонные изгибные
ж
3EI 1



 ёсткости
ij
= EIj
/ lj
эле-
ёсткости
ij
= EIj
/ lj
эле-
м
3
b3
e3
e4











 ентов
ОСМП:
ентов
ОСМП:
i
Z2 EI
3
Тип
2 1
=
1
=





i
Тип
1
2
4



3EI
3EI
b4
2

 На рис. 3.28
пока-
На рис. 3.28
пока-
з
b1 1
2
e1
e2
b2
b5















 аны
состояния ОСМП
аны
состояния ОСМП
п
Тип
2
Тип
2



 ри
единичных смеще-
ри
единичных смеще-
н
5 EI
Тип
2
в
e5
рис.
3.29 – 



 от единич-
от единич-
н
6
м
6



ловых факторов Jk = 1
( k = 1, 2, 3 ), а от ампли- Рис. 3.27
туд динамических на-
грузок и от снеговых нагрузок – на рис. 3.30. Там же даны соот-ветствующие эпюры изгибающих моментов.
Используя данные рис. 3.28 – 3.30, формируем исходные матрицы для расчёта рамы по программе METDEF кафедры стро-ительной механики НГАСУ ( Сибстрин ). При этом единичные инерционные воздействия, динамические и статические нагруз-ки ( кроме весов масс, учитываемых так, как описано на с. 158 ) рассматриваются как шесть вариантов загружения.
Z1
=
1
r11
r12
Z3
=
1
r13
r31
r32
r33










































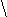


































r21
r23


Z2
=
1
r22























![]() =
1
=
1
![]() =
2
=
2
![]() =
3
=
3







4i4
=
4i
2i
3i3
=
6i
3i1
=
6i
6i1/l4
=
1,5i









4i4
=
4i



2i


3i2
=
6i
![]()

![]()

![]()
Рис. 3.28
![]()
![]()
![]()



![]()



















![]()
![]()























![]()





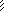



![]()





J1
=
1





![]() =
1
=
1
![]() =
2
=
2
![]()















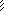













![]()





![]()
![]()

![]()
J3
=
1![]()

![]() =
3
=
3
![]()

Рис. 3.29
Flm
=
4,5
кНм
q
=
2
кН
/м
R3F
R1F
p(2)
=
8
кН
/м
R1p(1)
R1p(2)
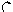



F
=
3
кН
R2p(1)
R3p(1)























































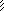





































R2F
p(1)
=
8
кН
/м
R2p(2)
R3p(2)







Fd
p(1)
p(1)

















![]()



![]()


![]()
![]()





![]()

![]()


(![]() )
(
)
(![]() )
(
)
(![]() )
)
Рис. 3.30
Исходные матрицы для расчёта по программе METDEF :
Элементы
от Z1=1 Z2=1 Z3=1 от Z1=1 Z2=1 Z3=1 от J1=1 J2=1 J3=1 F, q p(1) p(2)
