Задача 3.2. Динамический расчёт симметричной системы
F(t)
=
F
sin
F
t m m
2m
Требуется:
Составить с
учётом симметрии рамы
( рис.
3.32 )
основные уравнения для её динамических
расчётов при гармо-нических колебаниях.
3EI
п
q(t)
=
q
sin
F
t
м
EI EI
с
3EI m m
3EI
3EI
осредоточенные
мас-
с
EI EI
степени
свободы, из 
к l l
l
/
2
l
/
2
l
/
2
l
/
2
к
альные
перемещения
трех точечных
масс, а
Рис. 3.32
четвёртая – это общее
д
F
J3
y4
оженных
на верхнем ригеле рамы, их го-ризонтальное
перемещение. Следовательно,
при произвольных
( асимметричных
) воздействиях
число основных
неизвестных – перемещений
масс или инерционных силовых факторов
– равно четырём. Расчётная
схема
д m m
к
J4(1)
J4(3)
y3
р
2m q
J1
J4(2)
ис.
3.33 при амплитудных
н
J2
агрузках
и соответствую-
щ
y1 m m
р
y2
y4 и силах инерции J1 , J2 ,
J
3
, J4(1)
,
J4(2)
,
J4(3)
.
Учитывая,
что J4(1): J4(2): J4(3) = m :2m:m = Рис. 3.33
= 1 : 2 : 1 ), принимаем J4 = J4(1) +J4(2) + J4(3).
Рассмотрим описанные в п. 1.6 два варианта решения зада-чи с учётом симметрии системы.
Вариант А. Использование групповых неизвестных
При решении задачи в амплитудах инерционных сил две ис-ходные вертикальные силы инерции пары точечных масс m, сим-
метрично расположенных на нижнем ригеле рамы, заменяем дву-
м
m m F
и обратносимметричной
(
рис. 3.34
). В
качестве не-
и
2m
принимает-
с q
я
действующая
вдоль ли-
н m m
ии
симметрии
вертикаль-
н
исходной J3 . Четвёртое
о
сновное
неизвестное
–
с
Рис. 3.34
одной линии горизонталь-
ных сил инерции
трёх масс:
,
где
,
совершающих
одинаковые
горизонтальные
пе-
ремещения. Новые
( групповые
) неизвестные
связаны
с исход-ными
J
следующими
зависимостями:
или
тогда
матрица пре-
образования
неизвестных
,
матрица приве-
дённых масс (
см. п. 1.6
)
diag
[
m/2
m/2
2m
4m
].
Из четырёх
групповых неизвестных два – симметричные
(
и
),
два
–
обратносимметричные
(
и
).
Вследствие
этого
полная система основных уравнений вынужденных колебаний
распадается
на две
независимые
подсистемы
и
( см.
п. 1.6
), которые
для рас-
сматриваемой рамы записываются так:
и
где
В расчете на
собственные колебания
основные уравнения также распадаются
на две независимые системы
и
,
а общее
частотное
уравнение Det
(
)
=
0 порождает
уравнения Det
(
)
= 0 и Det
(
)
= 0, которые
принимают
следующий вид:
где
=
1/(
m2
).
Из первого уравнения определяются частоты симметричных главных форм собственных колебаний, а из второго – обратно-симметричных.
При использовании в расчёте на гармонические колебания уравнений в амплитудах перемещений масс группировке подвер-
гаются величины
y:
,
откуда
,
из
них
и
–
симметричные
перемещения
масс (
–
групповое,
–
одиночное
),
и
–
обратносимметричные.
Уравнения вынужденных
колебаний
распадаются
на две группы:
и
,
а в расчёте на собственные колебания получаются два независи-мых частотных уравнения
где
=
m
2
.
Вариант Б. Расчет половины системы
y
F(t)
/2
F(t)
/2
F(t)
/2
m m m
q(t)
/2
= 0
u
=
0
2m
q(t)
/2 m
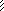
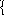
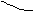
m m m
=
0
x
F(t)
/2
F(t)
/2 m m
v
=
0 m m
2m
q(t)
/2
F(t)
/2 m
q(t)
/2
б)
г)
q(t)
/2 m m
v
=
0
Рис. 3.35
В каждом случае сечением по оси симметрии система раз-деляется на две половины, одна из которых ( здесь – правая ) от-брасывается. Её влияние на оставшуюся ( левую ) половину моде-лируется связями, обеспечивающими выполнение кинематичес-ких условий в местах разреза стержней ( эти условия для сред-них сечений ригелей записаны на схемах рис. 3.35, а, б ). Усло-виям = 0 и u = 0 отвечает вертикально подвижное защемление ( рис. 3.35, в ), а v = 0 – вертикальная линейная связь ( рис. 3.35, г ).
Таким образом приходим к двум разным по опорным устройствам расчётным схемам половины заданной рамы ( рис. 3.35, в, г ), эквивалентным по НДС соответствующей части полной рамы в случаях симметричного и обратносимметричного движений. Далее выполняются независимые расчёты двух полу-ченных полурам, каждая с двумя степенями свободы масс.
Д о п о л н е н и е
Если массы в верхних узлах рамы не точечные ( рис. 3.36, а ),
т
y5
y6
степени
свободы, кото-рым
соответствуют
инерционные
моменты
J5
и
J6.
Заменив
их
груп-повыми
–
симметрич-
ными
обратносимметричны-
ми
мируем
расчётную
схе-му
(
рис.
3.36,
б
).
Ос-тальные
неизвестные связаны
зависимостями
и
,
фор-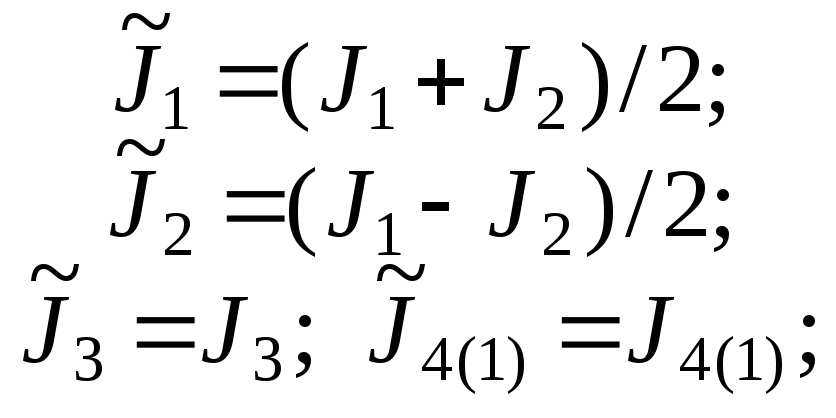
F
J3
y4 m m
J4(1)
J4(3)
J4(2)
y3
J5
J6
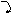
J2
2m q
y3
m
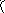
y2 m
J1
F
m m
2m
q
m m
Рис. 3.36
Матрица преобразования
восьми исходных неизвестных J
в
восемь
групповых
(
пока без
объединения
компонентов J4
и
):
Матрицу
приведённых масс определяем как
где
–
массы,
соответствующие исходным неизвестным.
Фор-мируя
,
учитываем,
что
инерционный
момент
J5
связан
с
силой инерции
J4(1)
, а J6
– с J4(3)
(
см. п. 1.0
):
неточечная
масса; Im0
– её собственный
момент инер-
ции; em
–
эксцентриситет
прикрепления к
узлу ).
(здесь
m
–
Выполнив умножение матриц, получаем:
Объединение
сил инерции
в
одну
матрично описывается как
,
где 4
= [
1 1 1
], тогда
матрица преобразования восьми группо-вых
неизвестных в окончательные шесть
:
4
Используем
её
для
вычисления
матрицы
приведённых
масс, порождающих
шесть групповых неизвестных:
.
Ту же матрицу
можно
получить, используя вместо квад-ратной
0
прямоугольную
матрицу
размерами 6 x
8:
этом, выполнив
матрич-
ную процедуру
–
предлагается убедиться в
Далее обращаем матрицу масс:
(
здесь Im
=
Im0
+
)
и, учитывая разделение групповых
неиз-вестных
на
симметричные
,
,
и обратносимметричные
,
,
,
составляем
уравнения для расчёта на гармонические
вынужденные колебания в
амплитудах инерционных сил:
и
где
;
=
Im
/(4Im0)
;
=
m
(2
–
)/Im0
;
=
– mem
/(2Im0)
(
определяются
компонентами
).
Для случая собственных колебаний получаются частотные уравнения
В динамическом расчёте по уравнениям в амплитудах пе-ремещений масс имеем для вынужденных колебаний:
,
;
уравнения частот собственных колебаний:
где = m 2 .