Задача 3.3. Динамический расчёт системы с взаимозависимыми перемещениями сосредоточенных масс

m₍₃₎

m₍₄₎

J₆

y₈

Требуется сформировать уравнения для расчёта на соб-ственные и гармонические вынужденные колебания системы с сосредоточенными массами, схема которой изображена на рис. 3.37, а.

l₁

l₂ /2

l₂ /2

J₈

J₇

y₆

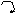
y₃

y₇

l_m

y₁

y₅

m₍₁₎

m₍₂₎

J₅

J₃

J₁

y₂

y₄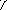

J₄

J₂



Рис.3.37

На рис. 3.37, б обозначены компоненты перемещений масс и инерционных силовых факторов, без учёта их возможной взаи-мозависимости, но в предположении отсутствия вертикального перемещения массы m₍₄₎. Используя обозначения, введённые в п. 1.6, вектор исходных перемещений масс формируем как вось-микомпонентный: y = [ y₁ y₂ y₃ y₄ y₅ y₆ y₇ y₈]^т , соответ-ствующий вектор исходных инерционных силовых факторов –

J = [ J₁ J₂ J₃ J₄ J₅ J₆ J₇ J₈]^т .

Их компоненты в случае собственных колебаний связаны

зависимостью J =(при гармонических вынужденных коле-

баниях  заменяется на _F ),

г

де .

Определяем число степеней свободы

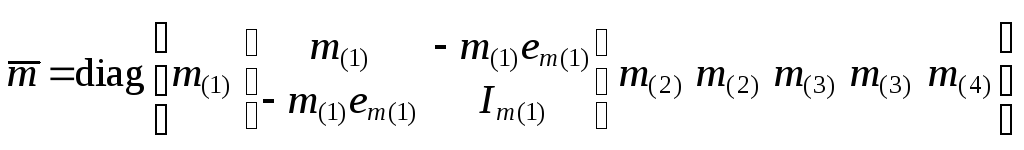масс как минимальное количество связей,

н

еобходимых для устранения возможных

перемещений масс ( рис. 3.38 ). Пренебре-

г

Рис. 3.38

ая продольными деформациями стерж-

н

ей, получаем n = 4. Следовательно, из 8 исходных компонентов перемещений четыре зависят от остальных. Приняв в качестве независимых перемещения, по направлениям которых постав-лены связи на рис. 3.38 и проанализировав взаимозависимости между перемещениями y, обозначенными на рис. 3.37, выражаем последние через : y₁ = y₂ = y₆ = y₃ = y₄ =

y₅ = y₇ = y₈ =

Матрица связи между векто-

рами исходных y и групповых ( об-

общённых ) перемещений масс:

Используем её для определе-

ния групповых инерционных сило-

вых факторов соответствующих

обобщённым перемещениям , и

для формирования матрицы приведённых масс порождающих

групповые По формулам ( 1.108 ) и ( 1.107 ):

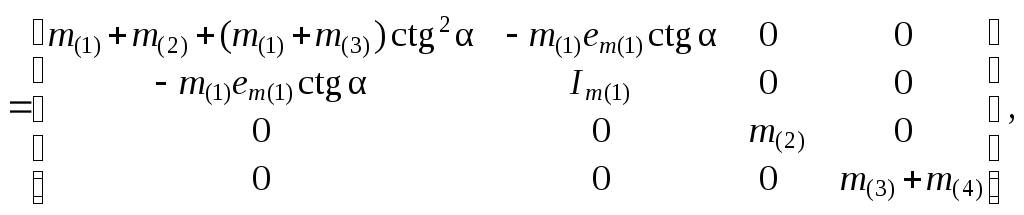
где I_m(1) = I_m0(1) + m₍₁₎ ( здесь I_m0(1) =e_m = l_m / 2 ).

Для контроля: при  = /2 ( левая нижняя стойка – вертикальная ) из вышепри-ведённых матриц получается = [ J₁+J₅ J₃ J₄ J₇ +J₈ ]^т – исчезают J₂ и J₆ , так как

становятся невозможными вертикальные перемещения масс m₍₁₎ и m₍₂₎ ( см. рис. 3.37 );

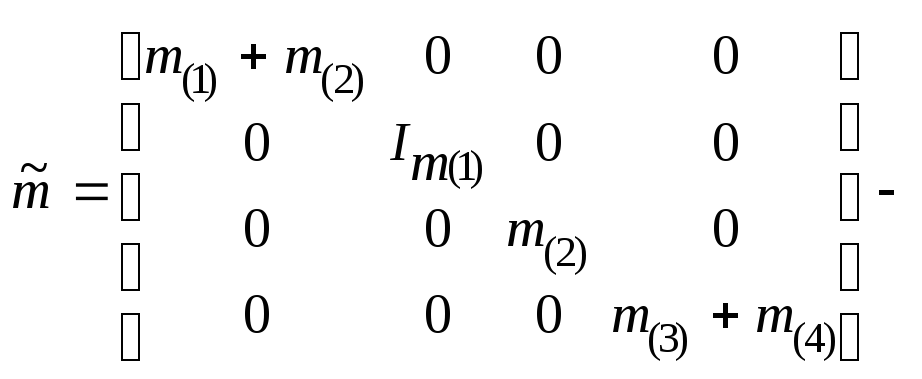смысл этих матриц очевиден.

Динамические расчёты рассматриваемой системы проще

выполнять по уравнениям в амплитудах перемещений:

для случая собственных колебаний и при вынуж-

денных колебаниях – с использованием основной системы МП,

п

Z₁ , Z₂ , Z₃ и Z₄ – это амплиту-ды независимых перемещений масс. Остальные – дополни-тельные ( угловые ) перемеще-ния расчётных узлов ОСМП.

Обратим внимание на то, что присутствующие в расчёт-ной схеме инерционные сило-вые факторы в явном виде в уравнения не входят, так как отражены в динамических по-правках в компонентах матриц

динамической жёсткости и ( см. п. 1.5.4.4 и п.1.5.5 ).

оказанной на рис. 3.39 ( без нагрузки ). Основные неизвестные

Z₅

Z₆

Z₁ =

Z₂ =

Z₃ =

Z₄ =

Z₇

Z₈

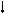
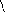
Рис. 3.39

Далее решение строится так, как описано в задаче 3.1,

в том числе с возможным переходом к уравнениям и

, относящимся к рассчитываемой системе, – путём

исключения дополнительных неизвестных Z_d = [ Z₅ Z₆ Z₇ Z₈ ]^т .

Единичные состояния ОСМП, необходимые для построения матрицы её жёсткости r₀ , изображены на рис. 3.40.

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

Z₂= 1

k₄₁

k₄₁

k₄₁

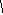
Z₁= 1

Z₃= 1

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

Z₄= 1

Z₆= 1

Z₅= 1

k₄₁

k₄₁

k₄₁

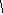
k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

k₄₁

Z₈= 1

k₄₁

k₄₁

k₄₁

k₄₁

Z₇= 1

k₄₁

k₄₁

k₄₁

Рис. 3.40

Матрицу динамической жёсткости системы при собствен-ных колебаниях формируем, используя матрицу жёсткости ОСМП r₀ и полученную ранее матрицу масс :

С и м м е т р и ч н о

где

Матрица динамической жёсткости при вынужденных гар-монических колебаниях отличается от частотой _F вместо .

Ненулевые единичные реакции r_{0, ik} определяются обычным по-рядком при конкретных числовых значениях геометрических и жесткостных параметров системы.

В варианте динамического расчёта по уравнениям в амп-литудах инерционных силовых факторов и

используется расчётная схема

по рис. 3.41. Весовые коэффи-

циенты k₁₁ , k₁₂ , …, k₄₂ компо-

нентов групповых сил инерции

и определяются из усло-

вия пропорциональности сил

инерции массам и перемеще-

ниям ( при гармонических коле-

баниях ): k₁₁ : k₁₂ : k₁₃ : k₁₄ =

Рис. 3.41

= m₍₁₎ y₁ : m₍₁₎ y₂ : m₍₂₎ y₅ : m₍₃₎ y₆ .

Учитывая, что y₁ = y₅ ( см.

рис. 3.37 ), y₂ = y₆ = y₁ctg  , получаем k₁₁ : k₁₂ : k₁₃ : k₁₄ =

= 1 : ctg  : m₍₂₎/m₍₁₎ : (m₍₃₎/m₍₁₎) ctg  . Значения k_1j находим из ус-ловия k₁₁ + k₁₂ + k₁₃ + k₁₄ = 1. Например, при  = /3 , m₍₂₎ = m₍₁₎ , m₍₃₎ = 0,5 m₍₁₎ : k₁₁ = k₁₃ = 0,3489; k₁₂ = 0,2015; k₁₄ = 0,1007. Осталь-ные коэффициенты: k₄₁ = m₍₃₎ / (m₍₃₎ + m₍₄₎); k₄₂ = m₍₄₎ / (m₍₃₎ + m₍₄₎).

k₁₄

Для определения компонентов

_ik матрицы упругой податливости  а)

р

k₁₁

k₁₃

ассчитываемой системы рассматри-

ваем её единичные состояния, изо-

б

k = 2

ражённые на рис. 3.42.

k₁₂

k₄₂

k₄₁

б) в) г)

k = 2

k = 2

k = 2

Рис. 3.42

После нахождения единичных силовых факторов от ( рис. 3.43 ) и вычисления по ним перемещений _ik подоб-

но тому, как это сделано в задаче 3.1, формируем матрицы дина-

Рис. 3.43

мической податливости для случаев собственных и гармоничес-ких вынужденных колебаний: и , где