Вопросы для самопроверки

1. Как определяется функция распределения случайной величины?

2. Какие другие названия используют для функции распределения?

3. Как с помощью функции распределения вычислить вероятность того, что случайная величина примет значение из полуинтервала ?

4. Какую случайную величину называют непрерывной?

5. Какими свойствами обладает функция распределения?

6. Какой вид имеет график функции распределения?

7. Чему равна вероятность того, что непрерывная случайная величина примет одно, заданное определенное значение?

8. Можно ли утверждать, что событие А является невозможным, если

9. Как определяется функция распределения для дискретной случайной величины?

10. Является ли непрерывной функция распределения для дискретной случайной величины?

11. Чему равны наименьшее и наибольшее значения функции распределения?

12. Что определяет величина скачка функции распределения дискретной случайной величины?

Упражнения

1. Даны функции

а) б) .

Являются ли эти функции функциями распределения некоторых случайных величин?

2. Закон распределения дискретной случайной величины задан таблицей

хi	0	1	2	3
рi	0,2	0,4	0,3	0,1

Найти функцию распределения этой случайной величины.

3. В партии из 10 деталей имеется 8 стандартных. Из этой партии наугад взято 2 детали. Найти функцию распределения дискретной случайной величины, равной числу стандартных деталей.

4. Случайная величина Х задана функцией распределения

Найти вероятность того, что в результате испытания величина Х примет значения из интервала (2, 3).

5. Трижды подбрасывается симметричная монета. Найти функцию распределения случайной величины Х, равной числу выпавших гербов.

6. Из 25 контрольных работ, среди которых 5 оценены на «отлично». наугад извлекают 3 работы. Найти функцию распределения дискретной случайной величины Х, равной числу оцененных на «отлично» работ среди извлеченных. Используя функцию распределения, найти вероятность события .

7. Непрерывная случайная величина Х задана функцией распределения :

Требуется найти значение параметра С, построить график функции, вычислить вероятность того, что в результате испытания случайная величина Х примет значение из интервала (0,3).

3. Плотность распределения вероятностей непрерывной случайной величины

Ранее непрерывная случайная величина задавалась с помощью функции распределения. Этот способ задания не является единственным. Непрерывную случайную величину можно также задать, использую другую функцию, которую называют плотностью распределения или плотностью вероятности (иногда ее называют дифференциальной функцией).

Плотностью распределения вероятностей непрерывной случайной величины Х называют функцию – первую производную от функции распределения .

Из этого определения следует, что функция распределения является первообразной для плотности распределения. Заметим, что для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима.

Можно показать, что вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b:

.

В частности, если – четная функция и концы интервала симметричны относительно начала координат, то

.

Геометрически этот результат можно истолковать так: вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу , равна площади криволинейной трапеции, ограниченной осью Ох, кривой распределения и прямыми и .

Пример 3.1. Задана плотность вероятности случайной величины Х

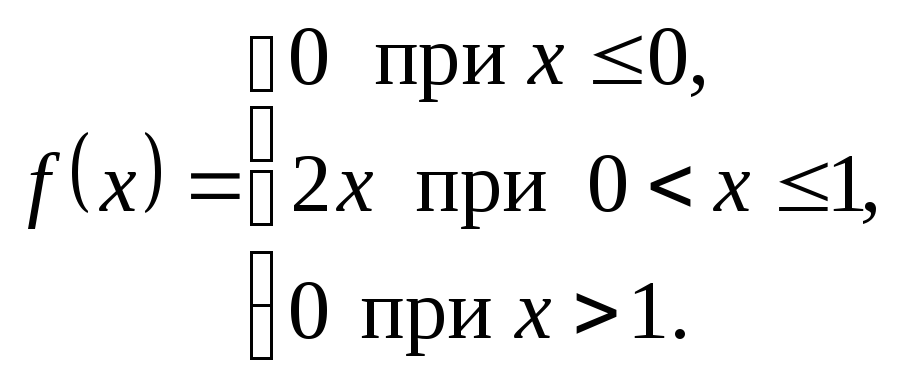
Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).

Искомая вероятность равна

.

Зная плотность распределения , можно найти функцию распределения по формуле

.

Пример 3.2. Найти функцию распределения по данной плотности распределения

Если , то и значит . Если , то , следовательно

.

Если , то

.

Итак, искомая функция распределения

Свойства плотности распределения:

1. Плотность распределения – неотрицательная функция, т. е.

Геометрически это свойство означает, что точки, принадлежащие графику плотности распределения, расположены либо над осью Ох, либо на этой оси. График плотности распределения называют кривой распределения.

2. Несобственный интеграл от плотности распределения в пределах от до равен единице:

.

Геометрически это означает, что вся площадь криволинейной трапеции, ограниченной осью Ох и кривой распределения, равна единице. В частности, если все возможные значения случайной величины принадлежат интервалу , то

.

Пример 3.3. Плотность вероятности случайной величины Х задана функцией

Найти постоянный параметр С.

Из свойства 2

.

Итак: .

Пусть – функция распределения непрерывной случайной величины Х. По определению плотности распределения , или в иной форме

.

Как известно, разность определяет вероятность того, что Х примет значение, принадлежащее интервалу . Таким образом, предел отношения вероятности того, что непрерывная случайная величина примет значение, принадлежащее интервалу , к длине этого интервала равен значению плотности распределения в точке х.

Итак, функция определяет плотность распределения вероятности для каждой точки х.

Из дифференциального исчисления известно, что приращение функции приближенно равно дифференциалу функции, т. е.

,

или .

Так как и ,

то .

Вероятностный смысл этого равенства таков: вероятность того, что случайная величина примет значение, принадлежащее интервалу , приближенно равна (с точностью до бесконечно малых высшего порядка относительно ) произведению плотности вероятности в точке х на длину интервала .

Геометрически этот результат можно истолковать так: вероятность того, что случайная величина примет значение, принадлежащее интервалу , приближенно равна площади прямоугольника с основанием и высотой .

Рис. 3.1

На рис. 3.1 видно, что площадь заштрихованного прямоугольни- ка, равная произведению , лишь приближенно равна площади криволинейной трапеции истинной вероятности, определяемой интегралом . Допущенная при этом погрешность равна площади криволинейного треугольника АВС.