3. Система Поста. Обчислюваність за Постом

Канонiчною системою Поста над алфавiтом T назвемо формальну систему (T*, A, P), у якій множина аксiом A є скiнченною підмножиною множини T*, а множина правил виведення P складається зі слiв вигляду ₀S₁₁..._m-1S_m_m. Тут T, усі _k та _і  фiксованi слова iз T* , усі символи S_kT, причому всi j_i{1,...,m}.

Символи S_k призначенi для позначення довiльних слiв iз T*.

Системи Поста звичайно позначають у вигляді P =(T, A, P).

Множина правил P визначає на словах iз T* вiдношення безпосереднього виведення таким чином: _Р , якщо iснує правило

₀S₁₁..._m-1S_m_mP,

таке, що для деяких слiв ₁, ..., _mT* маємо

=₀₁₁..._m_m , =.

Рефлексивно-транзитивне замикання вiдношення _Р позначаємо . Інакше кажучи,  означає, що слово  отримане зі слова  за допомогою скiнченної кiлькостi застосувань правил iз P.

Слово  породжується системою Поста P, якщо  для деякої A. Цей факт записуємо _P | та називаємо таке слово  теоремою системи Поста P.

Множину Th(P)={T*| _P |} називатимемо множиною теорем системи Поста P.

Для завдання системи Поста достатньо вказати множину правил та множину аксiом. У випадку необхiдностi вказуємо й алфавiт T.

Приклад 1. Система Поста iз A={a,b,} та P={SaSa, SbSb} породжує всi слова-палiндроми в алфавiтi {a,b}, тобто слова, якi читаються однаково злiва направо i справа налiво.

Множина X T* породжувана за Постом, якщо iснують алфавiт T'  T та система Поста P=(T', A, P), такi, що Th(P)(T*)=X.

Обчислюванiсть функцiй за Постом  це породжуванiсть за Постом графiкiв таких функцiй.

Часткова функцiя f : N^k→N обчислювана за Постом, якщо породжуваною за Постом є множина {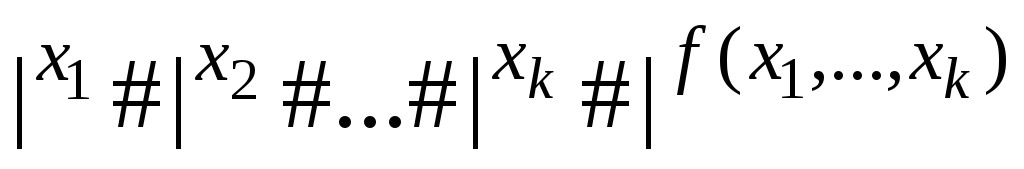(x₁,...,x_k)D_f }.

Наведемо приклади функцій і предикатів, обчислюваних за Постом.

Приклад 2. Система Поста для функцiї f(x, y)=x+y :

A ={##};

P ={X#Y#RX|#Y#R|,

X#Y#RX#Y|#R| }.

Приклад 3. Система Поста для функцiї f(x, y)=xy :

A ={##};

P ={X#Y#RX|#Y#R|,

X#Y#R|X#Y|#R }.

Приклад 4. Ще одна система Поста для функцiї f(x, y)=xy :

A ={##};

P ={X#Y#RX|#Y|#R,

X##RX|##R| }.

Приклад 5. Система Поста для предиката "x=y":

A ={## |};

P ={X#Y#RX|#Y|#R|,

X##RX|##,

#Y#R#Y|# }.

ЛЕКЦІЯ 4

ПЛАН

1. Поняття примітивно рекурсивної, рекурсивної й частково рекурсивної функцій (ПРФ, РФ і ЧРФ).

2. Алгебри ЧРФ та ПРФ.

1. Поняття примітивно рекурсивної, рекурсивної й частково рекурсивної функцій (ПРФ, РФ і ЧРФ)

Основними обчислюваними операцiями для п-арних функцiй на множині N є наступні операції: операція суперпозицiї Sⁿ⁺¹, операція примiтивної рекурсiї R, операція мiнiмiзацiї M.

Операцiя Sⁿ⁺¹ n-арнiй функцiї g(x₁,...,x_n) та n функцiям g₁(x₁,...,x_т), ..., g_n(x₁,...,x_m) одної i тої ж арностi ставить у вiдповiднiсть функцiю

f(x₁,...,x_m) = g(g₁(x₁,...,x_т), ..., g_n(x₁,...,x_m)).

Таку функцiю будемо позначати Sⁿ⁺¹ (g, g₁, ..., g_n), її арність збігається з арнiстю функцiй g₁, ..., g_n.

Операцiя примiтивної рекурсiї R n-арнiй функцiї g та (n+2)-арнiй функцiї h ставить у вiдповiднiсть (n+1)-арну функцiю f, яку позначають R(g,h), що задається рекурсивним визначенням

f(x₁,...,x_n,0) = g(x₁,...,x_n),

f(x₁,...,x_n,y+1) = h(x₁,...,x_n,y, f(x₁,...,x_n,y)).

Це означає, що для всiх значень a₁,..., a_n, b значення f(a₁,...,b_n ,b) обчислюється так:

f(a₁,...,a_n,0) = g(a₁,...,a_n),

f(a₁,...,a_n,1) = h(a₁,...,a_n,0, f(a₁,...,a_n,0)),

... ... ... ... ... ... ... ... ... ... ...

f(a₁,...,a_n ,b) = h(a₁,...,a_n ,b-1, f(a₁,...,a_n ,b-1)).

При n=0 вважаємо, що функцiя g  1-арна константа.

Операцiя мiнiмiзацiї M кожній (n+1)-арнiй функцiї g ставить у вiдповiднiсть n-арну функцiю f, яку позначають M(g), що задається спiввiдношенням

f(x₁,...,x_n) = _y(g(x₁,...,x_n,y)=0).

Це означає, що для всiх значень x₁, ..., x_n значення функцiї f(x₁,...,x_n) обчислюється так. Послiдовно обчислюємо значення g(x₁,...,x_n , y) для y=0, 1, 2, ... Перше таке значення y, для якого g(x₁,...,x_n , y)=0, буде шуканим значенням f(x₁,...,x_n). При цьому для всiх t<y значення g(x₁,...,x_n , t) мусять бути визначені та 0.

Із визначення випливає, що процес обчислення значення

_y(g(x₁,...,x_n , y)=0)

нiколи не закiнчиться в таких випадках:

значення g(x₁, ...,x_n , 0) не визначене;

для всiх значень у значення g(x₁,...,x_n , y) визначене та 0;

для всiх t<y значення g(x₁,...,x_n , t) визначене і 0, а значення g(x₁,...,x_n , y) не визначене.

Зрозуміло, що функцiя g може бути тотальною, а функцiя f=M(g)  навiть всюди не визначеною. Наприклад, f(x)=_y(x+y+1=0).

Базовими функцiями називаються найпростiшi функцiї о(x)=0, s(x)=x+1 та функцiї-селектори I(x₁,...,x_n)=x_m , де nm1.

Усi базовi функцiї тотальнi й алгоритмiчно обчислюванi.

Функцiю, яку можна отримати iз базових функцiй за допомогою скiнченної кiлькостi застосувань операцiй суперпозицiї та примiтивної рекурсiї, називають примiтивно рекурсивною функцiєю (скорочено ПРФ).

Функцiю, яку можна отримати iз базових функцiй за допомогою скiнченної кiлькостi застосувань операцiй суперпозицiї, примiтивної рекурсiї та мiнiмiзацiї, називають частково рекурсивною функцiєю (скорочено ЧРФ).

Тотальну ЧРФ називають рекурсивною функцiєю (скорочено РФ).

Iз наведених визначень випливають наступні твердження:

1. Якщо функцiї g, g₁, ..., g_n тотальнi та алгоритмiчно обчислюванi, то функцiя Sⁿ⁺¹(g, g₁, ..., g_n) тотальна й алгоритмiчно обчислювана.

2. Якщо функцiї g і h тотальнi та алгоритмiчно обчислюванi, то функцiя R(g, h) тотальна й алгоритмiчно обчислювана.

3. Якщо функцiя g алгоритмiчно обчислювана, то функцiя M(g) алгоритмiчно обчислювана.

4. Кожна ПРФ  тотальна алгоритмiчно обчислювана функцiя.

5. Кожна ЧРФ  алгоритмiчно обчислювана функцiя.

6. Кожна РФ  тотальна алгоритмiчно обчислювана функцiя.

7. Для відповідних класів функцій мають місце спiввiдношення ПРФРФЧРФ.