2. Геделеві нумерації чрф

Поняття геделевої нумерації для випадку нумерацій n-арних ЧРФ уточнимо таким чином.

Нумерація  геделева, якщо існують рекурсивні функції f і g, такі:

 для кожного тN = _f(m);

 для кожного kN _k = .

Це означає, що існує пара алгоритмів, перший із яких за стандартним індексом функції знаходить її -індекс, а другий за -індексом функції знаходить її стандартний індекс.

Твердження 2. Кожна геделева нумерація ефективна.

Справді, нехай нумерація  геделева. Тоді за ЧРФ, заданою стандартним індексом (кодом МНР-програми) т як , ефективно (використовуючи РФ f ) знаходимо її -індекс f(m); за -індексом k ефективно (використовуючи РФ g) знаходимо ЧРФ, задану кодом МНР-програми (стандартним індексом) g(m).

Нехай F  деякий клас функцій вигляду Х→Y, для якого задана нумерація :N→F. Із такою нумерацією  зв’язана функція и: N×Х→Y, що визначається умовою и(п,х) = _п(х). Зазначену функцію и називають спряженою з нумерацією .

Нумерація називається обчислюваною, якщо спряжена з нею функція є ЧРФ.

Твердження 3. Кожна геделева нумерація обчислювана.

Нехай нумерація  геделева, нехай g  РФ із визначення геделевої нумерації. Тоді спряжена до нумерації  функція и(п,х) = _п(х) =  є ЧРФ за тезою Чорча.

Зворотне твердження, взагалі кажучи, неправильне. Кожна обчислювана нумерація в певному смислі зводиться до геделевої, в той же час існують приклади негеделевих обчислюваних нумерацій. Проте такі приклади досить неприродні, вони використовують дуже штучні конструкції.

ЛЕКЦІЯ 9

ПЛАН

1. Поняття універсальної функції. Теорема про універсальні функції. Існування універсальної ЧРФ.

2. S-M-N-теорема, приклади її використання.

1. Поняття універсальної функції. Теорема про універсальні функції. Існування універсальної ЧРФ

Функцiя и(y, x₁, ..., x_п) називається унiверсальною функцiєю для класу F^п функцій із F фіксованої арності п, якщо:

 для кожного значення m функцiя и(y, x₁, ..., x_п) F^п;

 для кожної fF^п iснує таке m, що f(x₁, ..., x_n)=и(т, x₁, ..., x_п) для всiх значень x₁, ..., x_п .

Теорема 1. Нехай T  деякий клас тотальних п-арних функцiй на N, який мiстить функцiї о, s, I та замкнений вiдносно суперпозицiї. Нехай функцiя u унiверсальна для T^п. Тодi uT.

Припустимо супротивне: така uT, тобто uT^п+1. Визначимо функцiю g таким чином: g(x₁, ..., x_n)=и(x₁, x₁, ..., x_п)+1. Тодi gT^п. У силу унiверсальностi функцiї u iснує таке m, що g(x₁, ..., x_n)=и(т, x₁, ..., x_п) для всiх значень x₁, ..., x_п . Звiдси g(т, x₂,..., x_n) = =и(т, т, x₂, ..., x_п). Але за визначенням функцiї g g(т, x₂,..., x_n) = и(т, т, x₂, ..., x_п)+1. Дiстали суперечнiсть, бо функцiї g та u тотальнi.

Наслiдок 1. Функцiя, унiверсальна для класу n-арних РФ, не є ЧРФ.

Справдi, така функцiя тотальна i не є РФ.

Наслiдок 2. Функцiя, унiверсальна для класу n-арних ПРФ, не є ПРФ.

Теорема 2. Існує РФ, унiверсальна для класу n-арних ПРФ.

На основi розглянутої вище ефективної нумерацiї ПРФ задамо алгоритм для обчислення функцiї и(у, x₁, ..., x_п), унiверсальної для класу n-арних ПРФ. За п як кодом ОТ алгебри ПРФ побудуємо вiдповiдний ОТ i перевiримо, чи задає вiн n-арну ПРФ. Якщо нi, то видаємо значення 0 (тобто и(у, x₁, ..., x_п) – суть функцiя о^п ). Якщо так, то обчислимо значення заданої цим термом функцiї над x₁, ..., x_п . Отже, функцiя и  тотальна АОФ, тому за тезою Чорча вона рекурсивна.

Наслiдок 1. Існує РФ, яка не є ПРФ.

Наслiдок 2. Для вiдповiдних класiв функцiй маємо строгi включення ПРФРФЧРФ.

Теорема 3. Існує ЧРФ, унiверсальна для класу n-арних ЧРФ.

Розглянемо функцiю и(у, x₁, ..., x_п) = (x₁, ..., x_п). Вона є унiверсальною для класу n-арних ЧРФ. Справді, для кожного m функцiя и(т, x₁, ..., x_п)=(x₁, ..., x_п)  ЧРФ. З іншого боку, кожна n-арна ЧРФ f  суть функцiя  для деякого m, тобто f(x₁, ..., x_п) =(x₁, ..., x_п) = и(т, x₁, ..., x_п) для всiх x₁, ..., x_п .

Задамо алгоритм для обчислення функцiї u. За y як за кодом МНР-програми вiдновимо програму P_y для функцiї . Потiм запустимо P_y над значеннями x₁, ..., x_п . Отримане значення є значенням (x₁, ..., x_п). За тезою Чорча u  n-арна ЧРФ.

МНР-програма, яка обчислює унiверсальну ЧРФ, називається унiверсальною МНР-програмою. Унiверсальнiсть зовсiм не означає, що така програма мiстить у собi всi програми для обчислення n-арних ЧРФ! Унiверсальна програма вмiє декодувати довiльне число y в програму P_y , а далi вона моделює роботу P_y . Тому така унiверсальна програма може бути задана в явному виглядi. Отже, можна конструктивно знайти iндекс k унiверсальної функцiї u в стандартній нумерацiї (n+1)-арних ЧРФ, тобто u – суть функцiя .

Машина Тьюрiнга, яка обчислює унiверсальну ЧРФ, називається унiверсальною МТ. Таку МТ, здатну моделювати роботу довiльної МТ за її кодом, теж можна задати в явному виглядi.

Унiверсальна МНР-програма та унiверсальна МТ є абстрактними моделями сучасних комп’ютерiв. Вони реалiзують в абстрактному виглядi принцип програмного керування: виконання заданої програми над заданими даними.

2. S-M-N-теорема, приклади її використання

Теорема 4 (s-m-n-теорема). Для довiльних m, n>1 iснує (m+1)-арна РФ s(z, x₁,..., x_m), така, що для всiх z, x₁, ..., x_т, у₁, ..., у_п (x₁, ..., x_т, у₁, ..., у_п) =(у₁, ..., у_п).

Приклад 1. Залежнiсть функцiї s вiд n можна зняти, якщо для завдання ЧРФ використати МТ.

Справді, за z визначаємо МТ із кодом z для функцiї . Задамо нову МТ M, яка злiва вiд початкового вмiсту стрiчки дописує слово 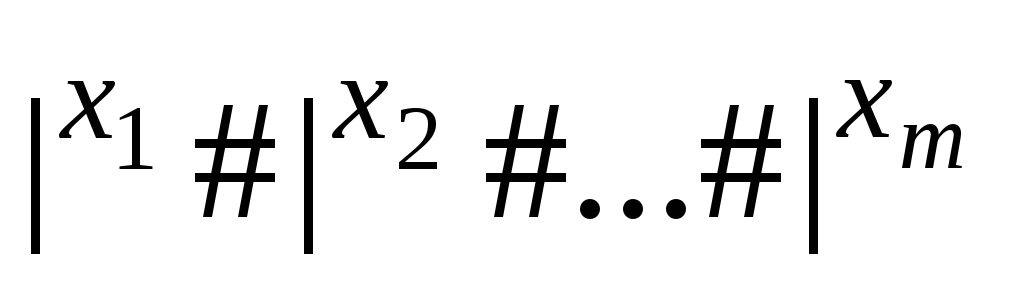, a далi моделює роботу МТ із кодом z. Така МТ M при входi 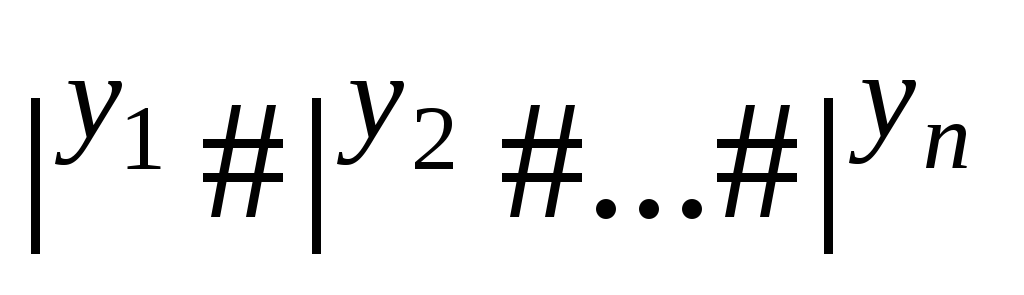обчислює n-арну функцiю , причому k код МТ M  не залежить вiд n .

Теорема 5 (s-m-n-теорема в спрощенiй формi). Для кожної ЧРФ f(x₁, ..., x_т, у₁, ..., у_п) iснує РФ s(x₁, ..., x_m) така, що для всiх x₁, ..., x_т, у₁, ..., у_п маємо f(x₁, ..., x_т, у₁, ..., у_п) = (у₁, ..., у_п).

При т=п=1 спрощена s-m-n-теорема формулюється так:

Теорема 6. Для кожної ЧРФ f(x, y) iснує РФ s(x) така, що для всiх значень x, y маємо f(x, y)= _s(x)(y).

Розглянемо приклади застосування s-m-n-теореми.

Приклад 2. Існує РФ s(x, y) така, що для всіх х, y, zN маємо _s(x,y)(z)=_x(z)+_y(z).

Розглянемо функцію f(x, y, z) = _x(z) + _y(z). Функція f є ЧРФ, тому за s-m-n-теоремою існує РФ s(x, y) така, що для всіх х, y, zN маємо f(x, y, z)=_s(x,y)(z)=_x(z)+_y(z).

Приклад 3. Для кожної 1-арної ЧРФ f існує РФ s(x), така, що для всіх хN маємо D_s(x)= f ^-1(D_x).

Розглянемо функцію g(x, y) = _x(f(y)). Така функція є ЧРФ за ТЧ, тому за s-m-n-теоремою існує РФ s(x) така, що для всіх х, yN g(x, y) = _s(x)(у). Зафіксуємо х. Mаємо

уD_s(x)  _s(x)(у)  g(x, y)  _x(f(y))  f(y)D_x  yf ^-1(D_x).

Звідси D_s(x)= f ^-1(D_x).

Приклад 4. Існує РФ s(x) така, що для всіх хN маємо Е_s(x)=D_x .

Розглянемо функцію f(x, y)=Така функція є ЧРФ за ТЧ, тому за s-m-n-теоремою існує РФ s(x) така, що для всіх х, yN маємо f(x, y)=_s(x)(у). Зафіксуємо х. За побудовою функції f маємо D_s(x)=Е_s(x). Тепер уЕ_s(x)  уD_s(x)  _s(x)(у)  f(x, y)  уD_x .

Звідси Е_s(x)=D_x .

Приклад 5. Існує РФ t(x) така, що для всіх хN маємо D_t(x)=Е_x .

Розглянемо функцію f(x, y)= Така функція є ЧРФ за ТЧ, тому за s-m-n-теоремою існує РФ t(x) така, що для всіх х, yN f(x, y)=_t(x)(у). Зафіксуємо х. Mаємо уD_t(x)  _t(x)(у)  f(x, y)  уE_x . Звідси D_t(x)=E_x .

Приклад 6. Існує РФ s(x) така, що для всіх хN маємо

={(u, v) | x=2u+3v}.

Розглянемо функцію f(x, u, v)=

За ТЧ f є ЧРФ, тому за s-m-n-теоремою існує РФ s(x) така: для всіх х, u, vN f(x, u, v)=(u, v). Зафіксуємо х. Тепер

(u, v)  (u, v)  f(x, u, v)  x=2u+3v.

Звідси ={(u, v) | x=2u+3v}.

Приклад 7. Існує РФ s(x, y) така, що для всіх х, yN маємо D_s(x,y)=D_xD_y .

Розглянемо функцію f(x, y, z)= Така функція є ЧРФ за ТЧ, тому за s-m-n-теоремою існує РФ s(x, y) така, що для всіх х, y, zN маємо f(x, y, z)= =_s(x,y)(z). Зафіксуємо х та y. Маємо

zD_s(x,y)  _s(x,y)(z)  f(x, y, z)  zD_xD_y .

Звідси випливає D_s(x,y)=D_xD_y .

Приклад 8. Існує РФ s(x, y) така, що для всіх х, yN маємо D_s(x,y)=Е_s(x,y)=D_xD_y .

Розглянемо функцію f(x, y, z)= Така функція є ЧРФ за ТЧ, тому за s-m-n-теоремою існує РФ s(x, y) така, що для всіх х, y, zN маємо f(x, y, z)=_s(x,y)(z). Зафіксуємо х та y. За побудовою функції f маємо D_s(x,y)=Е_s(x,y). Тепер

zЕ_s(x,y)  zD_s(x,y)  _s(x,y)(z)  f(x, y, z)  zD_xD_y .

Звідси отримуємо D_s(x,y)=Е_s(x,y)=D_xD_y .

ЛЕКЦІЯ 10

ПЛАН

1. Теореми Кліні про нерухому точку.

1. Теореми Кліні про нерухому точку

Теорема 1. Нехай f  (n+1)-арна РФ. Тодi iснує n-арна РФ g, така, що для всiх значень x₁, ..., x_п маємо = .

За s-m-n-теоремою iснує РФ s(и, x₁, ..., x_п) така, що для всiх u, x₁, ..., x_п, y маємо

= . (1)

Нехай функцiя f(s(x₁,..., x_п), x₁, ..., x_п) має iндекс k у нумерацiї (n+1)-арних ЧРФ, тобто це функцiя (u, x₁, ..., x_п). За тотальнiстю функцiй f та s функцiя  тотальна. Тому при u=k для всiх x₁, ..., x_п маємо

f(s(x₁,..., x_п), x₁, ..., x_п) = (k, x₁, ..., x_п). (2)

Iз (1) при u=k та iз (2) дiстаємо

= = 

для всiх x₁, ..., x_п . Отже, функцiя g(x₁, ..., x_п) = s(k, x₁, ..., x_п)  шукана РФ.

Для випадку n=0 теорема 1 переформульовується так:

Теорема 2. Нехай f(x)  РФ. Тодi iснує nN таке, що _n = _f(n).

Наведену теорему Клiнi про нерухому точку краще називати теоремою про псевдонерухому точку. Справдi, умова _n=_f(n) зовсiм не означає, що n=f(n), a свiдчить тiльки про те, що n i f(n)  iндекси одної i тої ж ЧРФ.

Теорему про нерухому точку називають також теоремою про рекурсiю, бо вона виражає рекурсивне визначення дуже загального вигляду. Наприклад, визначимо функцiю _n через задану РФ f так: _n=_f(n) . Тодi _n ефективно визначена через n  код МНР-програми для її обчислення, бо таке n iснує згiдно з теоремою 2.

Наслiдок 1. Нехай f(x)  РФ. Тодi iснує nN таке, що D_n = D_f(n) та E_n = E_f(n).

Справдi, згiдно з теоремою 2 досить узяти nN таке, що _n = _f(n) .

Наслiдок 2. Нехай h(z, x)  ЧРФ. Тодi iснує nN таке, що для всiх x h(n, x)=_n(x).

За s-m-n-теоремою iснує РФ s(z) така, що h(z, x) = _s(z)(x) для всiх z, x. За теоремою 2 iснує таке n, що _n = _s(n) , тобто h(n, x) = _s(n)(x) = _n(x) для всiх x .

Зауважимо, що формулювання наслідку 2 це первісне формулювання самого С.Кліні теореми про нерухому точку. Покажемо, що наслідок 2 та теорема 2 еквівалентні. Для цього виведемо теорему 2 із наслідку 2.

Нехай f(x)  РФ. Тоді за тезою Чорча функція h(z, x)=_g(z)(x) є ЧРФ. За наслідком 2 існує nN таке, що для всiх x h(n, x)=_n(x), тобто для всiх x h(п, x) = _g(п)(x) = _n(x).

МНР-програма P самотворна, якщо для довiльного xN маємо P(x)(P), де (P)  код програми P. На перший погляд, таких програм бути не може, бо для побудови P треба знати (P), тобто саму програму P. Проте самотворнi програми таки iснують!

Теорема 3. Існує МНР-програма P така, що P(x)(P) для всiх значень x.

Вiзьмемо функцiю h(z, x) = z. За наслiдком 2 iснує таке n, що для всiх x h(n, x)=_n(x). Отже, _n(x) = h(n, x) = n для всiх x. Тому програма P із кодом n  шукана.

Покажемо тепер, що нерухома точка кожної РФ _n ефективно залежить вiд її iндексу n. Це посилює твердження теореми 2.

Теорема 4. Існує РФ (x) така: для кожного nN, якщо _n є РФ, то _(n)=.

За s-m-n-теоремою iснує РФ s(x) така, що

= _s(x)(y) для всiх x, yN. (1)

Тодi за s-m-n-теоремою iснує РФ (x), для якої

_n(s(x)) = _(n)(x) для всiх n, xN . (2)

Якщо _n є РФ, то кожне значення _n(x) визначене. Взявши x=(n), iз (1) маємо

_s((n)) (3)

та iз (2) маємо _n(s((n))) = _(n)((n)). Звiдси та із (3) дiстаємо _s((n))=. Поклавши (x)= s((x)), маємо _(n) =.

Покажемо, що для кожної РФ можна ефективно знайти монотонно зростаючу послiдовнiсть її нерухомих точок. Звiдси, зокрема, випливає нескiнченнiсть множини нерухомих точок кожної РФ.

Теорема 5. Для кожної РФ f(x) iснує строго монотонна РФ (x), така, що для кожного nN маємо _(n) =_f((n)).

За s-m-n-теоремою iснує РФ s(x) така: _s(x)(y) для всiх x, yN. Нехай m  деякий iндекс функцiї s(x), тобто s(x) – суть _m(x). Звiдси для всiх yN, тобто _m(m)  нерухома точка функцiї f. Згiдно із зауваженням 1 до s-m-n-теореми s(x)x для всiх xN, тому _m(m)m.

Функцiю (x) задамо так:

(0) = , де m₀ – довiльний iндекс функцiї s;

(k+1) = , де m_k+1  такий iндекс функцiї s, що m_k+1>(k)

(у силу твердження 1 такий iндекс знаходиться ефективно).

Кожне значення функцiї  є нерухомою точкою функцiї f. Функцiя  алгоритмiчно обчислювана, вона тотальна в силу тотальностi функцiї s. За ТЧ  є РФ, причому для всiх kN (k+1)= m_k+1>(k). Тому   строго монотонна РФ.

Наслiдок. Для кожних РФ f(x) та kN iснує nN таке, що n>k та _n=_f(n).

Розглянутi нами ефективнi нумерацiї ЧРФ неоднозначнi. Однозначнi ефективні нумерацiї ЧРФ iснують, але немає в певному смислi "природних" однозначних ефективних нумерацiй ЧРФ.

Теорема 6. Нехай f(x)  строго монотонна тотальна функцiя, для якої виконуються умови:

1) якщо mn, то _f(т)_f(n); 2) f(n)  найменший iндекс функцiї _f(n) .

Тодi функцiя f не є ЧРФ.

Функцiя f не може бути тотожною, бо тодi з умови mn випливає _m_n . Тому iснує таке kN, що f(n)>n при nk. Але f(n)  найменший iндекс функцiї _f(n) , тому _f(т)  _f(n) для всіх nk. Якщо f рекурсивна, то за наслiдком теореми 5 iснує nN таке, що n>k і _f(n)=_n . Дiстали суперечнiсть, тому функцiя f не є РФ та не є ЧРФ.

Спiльної нерухомої точки для двох довiльних РФ може не бути. Нехай  і   рiзнi РФ, нехай k і m  iндекси функцiй  і , тобто =_k та =_m . Вiзьмемо функцiї-константи f(x)=k і g(x)=m. Якщо iснує спiльна нерухома точка n для f і g, то _n = _f(n) та _n = _g(n). Звiдси =_k=_f(n)=_n=_{g(n )}= _m= , що суперечить припущенню  .

Проте можна знайти пару ефективно зв’язаних нерухомих точок для пари заданих РФ:

Теорема 7 (про парну рeкурсiю). Для кожної пари РФ f(x) і g(x) iснують m, nN такi, що _m = _f(C(m,n)) та _n = _g(C(m,n)) .

За s-m-n-теоремою iснує РФ s(x, y) така:

_f(C(x,y))(z) = _s(x,y)(z) для всiх x, y, zN . (1)

За теоремою 1 для РФ s(x, y) iснує РФ (y) така, що _(y) = _s((y),y) для всiх yN. Ураховуючи (1), звiдси маємо:

_(y) = _{f(C((y),y))} для всiх yN . (2)

За s-m-n-теоремою iснує РФ k(y) така:

_{g(C((y),y))}(z) = _k(y)(z) для всiх y, zN . (3)

За теоремою 2 для РФ k(y) iснує nN таке, що _n = _k(n). Звiдси, враховуючи (3), маємо _n = _{g(C((п),п))} . Покладемо m=(n). Тодi з _n = =_{g(C((п),п))} при y = n дістаємо _n = _g(C(т,п)) та з (2) при y = n маємо _т=_(т) = _{f(C((п),п))} = _f(C(т,п)) .

ЛЕКЦІЯ 11

ПЛАН

1. Поняття примітивно рекурсивної, рекурсивної та рекурсивно перелічної множини (ПРМ, РМ і РПМ).

2. Еквівалентні визначення РПМ.

3. Властивості ПРМ, РМ та РПМ.

1. Поняття примітивно рекурсивної, рекурсивної і рекурсивно перелічної множини (ПРМ, РМ та РПМ)

Множину MNⁿ називають рекурсивною (скорочено РМ), якщо її характеристична функцiя _M рекурсивна.

Множину MNⁿ називають примiтивно рекурсивною (скорочено ПРМ), якщо її характеристична функцiя _M примiтивно рекурсивна.

Зрозумiло, що кожна ПРМ є рекурсивною множиною.

Множину MN називають рекурсивно перелiчною (скорочено РПМ), якщо M= або M=E_f для деякої рекурсивної функцiї f.

Множину MNⁿ називають РПМ, якщо M= або iснують 1-арнi РФ g₁, ..., g_n такi, що M={(g₁(x), ..., g_n(x)) | xN }.

Як наслiдки тези Чорча дiстаємо такi твердження:

 клас РМ збігається з класом алгоритмiчно розв’язних множин натуральних чисел;

 клас РПМ збігається з класом алгоритмiчно перелiчних множин натуральних чисел.

Для кожної LNⁿ визначимо множину-згортку

Cⁿ(L)={Cⁿ(x₁, ..., x_n) | (x₁, ..., x_n)L}.

Нехай LNⁿ та MNⁿ. Безпосередньо iз визначень випливає:

Cⁿ(LM)=Cⁿ(L)Cⁿ(М), Cⁿ(LM)=Cⁿ(L)Cⁿ(М), Cⁿ(Nⁿ\L)=N\Cⁿ(L).