1. Програмні алгебри. Примітивні програмні алгебри

Програмна алгебра (P, C) задається парою (B, C), де множина функцій P  основа алгебри, C  множина композицiй (операцiй) над функцiями із P, BP  множина базових функцiй. Примiтивні програмні алгебри (ППА) - це програмнi алгебри функцiй із простими типами даних. До таких функцiй належать, зокрема, квазіарні, Х-арні та п-арні функцiї, заданi на неструктурованих множинах (наприклад, на множині N, на множинi R). Kомпозицiями ППА є операцiї суперпозицiї, циклу і розгалуження.

Операцiї суперпозицiї  це описані вище операцiї S.

Для випадку п-арних функцій N операцiї суперпозицiї, циклу й розгалуження дамо наступним чином.

Операцiя циклу ^N☼ n-арним функціям g та  ставить у вiдповiднiсть n-арну функцiю f, значення f(x₁, ..., x_n) якої для кожного набору значень x₁, ..., x_n визначається як перший елемент а_m послідовності

a₀=x₁, a₁=f(a₀, x₂, ..., x_n), a₂=f(a₁, x₂, ..., x_n), ..., a_k=f(a_k-1, x₂, ..., x_n), ...

такий, що (a_m, x₂,..., x_n)=0 та для всiх k<m значення (a_k, x₂, ..., x_n) визначене і 0, якщо такий елемент a_m iснує. Якщо такий елемент a_m не iснує, значення f(x₁, ..., x_n) не визначене.

Операцiя розгалуження ^N n-арним функцiям g, h і  ставить у вiдповiднiсть n-арну функцiю f, значення f(x₁, ..., x_n) якої для кожного набору значень x₁, ..., x_n визначається так:

f(x₁, ..., x_n) =

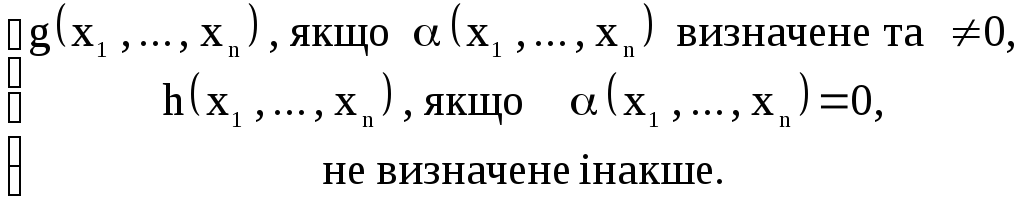
Базовими функцiями для випадку n-арних функцiй, заданих на множинi N, будемо вважати функцiї о, s та I, де nm1, а також бінарні функції +,  .

2. Програмовані функції

Функцiю назвемо програмованою на N, якщо її можна отримати iз указаних вище базових функцiй за допомогою скiнченної кiлькостi застосувань операцiй суперпозицiї Sⁿ⁺¹, розгалуження ^N, циклу ^N☼.

Із наведених визначень випливають наступні твердження:

1. Якщо функцiї , g, h алгоритмiчно обчислюванi, то функцiя ^N(, g, h) алгоритмiчно обчислювана.

2. Якщо функцiї  та g алгоритмiчно обчислюванi, то функцiя ^N☼(, g) алгоритмiчно обчислювана.

3. Кожна програмована на N n-арна функцiя є алгоритмiчно обчислюваною.

Алгебра (_N ; ^N, ^N☼, S², S³, ... ), носiєм _N якої є клас усiх програмованих на N n-арних функцiй, а операцiями  операцiї ^N, ^N☼ та Sⁿ⁺¹, де n1, називається примiтивною програмною алгеброю програмованих на N n-арних функцiй (ППА-Ar-N).

Дамо індуктивне визначення операторного терма ППА-Ar-N (ОТ ППА-Ar-N). Алфавiт складатиметься iз символiв базових функцiй о, s +,  та I, де nm1, символiв операцiй ^N, ^N☼ і Sⁿ⁺¹, де n1, а також допомiжних символiв (, ) та , .

1) кожен символ базової функцiї є ОТ; такі ОТ назвемо атомарними;

2) якщо t₀, t₁, ..., t_n ОТ, то Sⁿ⁺¹(t₀, t₁, ..., t_n)  ОТ;

3) якщо t₀, t₁ і t₂  ОТ, то ^N(t₀, t₁, t₂)  ОТ;

4) якщо t₀ та t₁ ОТ, то ^N☼(t₀, t₁)  ОТ.

Кожна програмована на N п-арна функція є значенням деякого ОТ ППА-Ar-N. Проте, як і у випадку ОТ алгебри п-арних ЧРФ, через порушення умов арності не кожен ОТ ППА-Ar-N має певне значення. Зрозуміло, що подання програмованих на N п-арних функцій операторними термами ППА-Ar-N неоднозначне.

Нехай функції  та  трактуються як предикати. Тоді функції nsg(),  і + можна трактувати як предикати , & та  відповідно. Враховуючи, що  можна подати як ,  можливо подати як ()&(), легко отримати функції, які моделюють указані предикати.

Приклад 1. Функції-константи програмовані.

Такі функції отримуються із базових функцій о, s та I за допомогою операцій Sⁿ⁺¹.

Приклад 2. Функції пsg(x₁) та sg(x₁) програмовані.

Справді, пsg(x₁)=, sg(x₁)=(.

Приклад 3. Функцiя |x₁-x₂| програмована.

Справдi, |x₁-x₂| = ()+().

Приклад 4. Предикати x₁>x₂, x₁x₂, x₁=x₂ та x₁x₂ програмовані.

Предикат x₁>x₂ моделюється функцiєю . Предикат x₁x₂ моделюється функцiєю , предикат x₁=x₂ можна подати у вигляді (x₁x₂)&(x₂x₁), предикат x₁x₂  у вигляді (x₁=x₂).

Приклад 5. Функція mod(x₁, x₂) програмована.

Функцію mod(x₁, x₂) можна подати операторним термом

^N☼(S³(, S²(s, I), I),).

Приклад 6. Функцiю x₁+x₂ можна отримати із базових функцій о, s, I,  за допомогою операцій ^N☼ та Sⁿ⁺¹.

Оскільки x₁<x₂+x₃  nsg(((x₁+1)))=1, предикат x₁<x₂+x₃ моделюється функцією nsg(((x₁+1))), ОТ  якої має вигляд

S³(, 1³, S³(, S³(, S²(s, I), I), I)).

Тому x₁+x₂ можна подати OT S⁴(^N☼(, S²(s, I)), о², I, I). Отже, функцію + можна не включати до базових програмованих на N п-арних функцiй.

Приклад 7. Аналогічно випадку V-квазіарних функцій, функцію f=^N(, g, h) можливо подати у вигляді f=gsg()+hnsg(). Отже, операцiю розгалуження ^N можна промоделювати, використовуючи базові функції о, s, I,  й операції суперпозицiї та циклу.

ЛЕКЦІЯ 6

ПЛАН

1. Поняття нумерації. Канторові нумерації пар та n-ок натуральних чисел.

2. Функція Геделя та її основна властивість.

3. Теорема про представлення операції примітивної рекурсії.