2. Властивості прп, рп та чрп
Тeорeма 1. 1) предикат P є ЧРП (РП, ПРП) IP є РПМ (вiдповiдно РП, ПРМ);
2) класи ПРП та РП замкненi вiдносно логiчних операцiй , &. та ;
3) клас ЧРП замкнений вiдносно операцiй і &;
4) клас ПРП строго включається в клас РП;
5) кожний рекурсивний предикат є ЧРП;
6) якщо P та P ЧРП, то P і P РП.
Твердження 1) безпосередньо випливає із визначень.
Нехай
IP
та IQ
областi iстинностi предикатiв P
і Q.
Тодi IP
IQ
область істинності предиката PQ,
IP
IQ
область iстинностi предиката P&Q,
область iстинностi предиката P.
Ураховуючи твердження 1), дістаємо, що
твердження 2) випливає з теореми 3 лекції
11 , твердження 3) випливає з теореми 11
лекції 11, твердження 4) та 5) випливають
iз теореми 2 лекції 11, твердження 6)
випливає з теореми Поста.
Тeорeма 2. Предикат Q(x1, ..., xn) частково рекурсивний тодi i тiльки тодi, коли iснує рекурсивний предикат R(x1, ..., xn, y) такий, що Q(x1, ..., xn) yR(x1, ..., xn, y).
Нехай
Q
ЧРП, нехай
обчислюється МНР-програмою P.
Уведемо предикат R(x1,
..., xn,
y),
що означає: P(x1,
..., xn)
за k
крокiв. Тодi Q(x1,
..., xn)
yR(x1,
..., xn,
y).
Але
алгоритмiчно обчислювана, тому
є РФ за ТЧ. Звiдси R
є РП.
Нехай
тепер R(x1,
..., xn,
y)
РП, нехай Q(x1,
..., xn)
yR(x1,
..., xn,
y).
Тодi Q(x1,
..., xn)
.
R(x1,
..., xn,
y)=1.
Тому функцiя f(x1,
..., xn)=s(o(y(nsg(R(x1,
..., xn,
y))=0))
частковa характеристичнa функцiя
предиката yR(x1,
..., xn,
y).
Але R
є РФ, тому f
є ЧРФ. Але f=
,
тому Q
є ЧРП .
Тeорeма 3. Нехай Q(x1, ..., xn, y) ЧРП. Тодi yQ(x1, ..., xn, y) теж ЧРП.
Якщо Q(x1, ..., xn, y) є ЧРП, то за теоремою 2 iснує РП R(x1, ..., xn, y, z) такий, що маємо Q(x1, ..., xn, y) zR(x1, ..., xn, y, z). Поклавши u=C(y, z), маємо співвідношення yQ(x1, ..., xn, y) yzR(x1, ..., xn, y, z) uR(x1, ..., xn, l(и), r(и)). Але l та r ПРФ, предикат R(x1, ..., xn, y, z) РП, тому предикат R(x1, ..., xn, l(и), r(и)) теж РП. Тодi предикат uR(x1, ..., xn, l(и), r(и)), а з ним i предикат yQ(x1, ..., xn, y) є ЧРП за теоремою 2.
Наслідок. Якщо предикат Q(x1, ..., xn, y) ЧРП, то предикат y1...ykQ(x1, ..., xn, y1, ..., уk) теж ЧРП.
Тeорeма 4. Функцiя f(x1, ..., xn) частково рекурсивна предикат "y= f(x1, ..., xn)" є ЧРП.
Нехай f(x1, ..., xn) є ЧРФ, нехай P МНР-програма для f. Тодi маємо y= f(x1, ..., xn) k(P(x1, ..., xn)y за k крокiв). Але предикат "P(x1, ..., xn)y за k крокiв" РП. Тому предикат k(P(x1, ..., xn)y за k крокiв), тобто предикат "y= f(x1, ..., xn)" є ЧРП.
Нехай предикат "y= f(x1, ..., xn)" ЧРП. За теоремою 2 iснує РП R : y= f(x1, ..., xn) zR(x1, ..., xn, y, z). Покладемо t= C(y, z), тодi y=f(x1, ..., xn) tR(x1, ..., xn, l(t), r(t)).
Покладемо g(x1, ..., xn, t)=nsg(R(x1, ..., xn, l(t), r(t))). Тодi маємо tR(x1, ..., xn, l(t), r(t)) t(y=l(t) та g(x1, ..., xn, t)=0). Узявши перше таке t, маємо t(y=l(t) та g(x1, ..., xn, t)=0) y=l(t(g(x1, ..., xn, t)=0)). Отже, y= f(x1, ..., xn) y=l(t(g(x1, ..., xn, t)=0)), тому f є ЧРФ.
Тeорeма 5 (теорема Клiнi про нормальну форму). Для кожної n-арної ЧРФ f iснує (n+1)-арна РФ g така, що для всiх x1, ..., xn N f(x1, ..., xn)=l(t(g(x1, ..., xn, t)=0)).
У цьому випадку подання l(t(g(x1, ..., xn, t)=0)) називають нормальною формою (скорочено НФ) функцiї f(x1, ..., xn).
Згiдно з теоремою 4 "y= f(x1, ..., xn)" ЧРП, тому для деякого РП R y= =f(x1, ..., xn) zR(x1, ..., xn, y, z). Покладемо g(x1, ..., xn, t)=nsg(R(x1, ..., xn, l(t), r(t))). Повторюючи доведення теореми 4, маємо
y= f(x1, ..., xn) y=l(t(g(x1, ..., xn, t)=0)).
Отже, f(x1, ..., xn)=l(t(g(x1, ..., xn, t)=0)).
Функцiю g у формулюваннi теореми Клiнi про НФ насправдi можна брати ПРФ. Доведення такого посиленого варiанта теореми. В цьому випадку теорема Клiнi про НФ засвiдчує, що кожну ЧРФ можна отримати iз деякої ПРФ не бiльше нiж одним застосуванням операцiї мiнiмiзацiї, причому певним стандартним чином.
ЛЕКЦІЯ 13
ПЛАН
-
Алгоритмічна розв’язність та нерозв’язність масових проблем.
-
Проблема зупинки та самозастосовності, їх нерозв’язність. Наслідки нерозв’язності.
-
Алгоритмічна розв’язність та нерозв’язність масових проблем
Масову проблему назвемо алгоритмiчно розв’язною, або розв’язною, якщо вiдповiдний предикат рекурсивний, iнакше проблему назвемо алгоритмiчно нерозв’язною, або нерозв’язною. Масову проблему назвемо частково алгоритмiчно розв’язною, або частково розв’язною, або напіврозв’язною, якщо вiдповiдний предикат частково рекурсивний. Наприклад, проблеми "x є квадратом натурального числа" та " P(x1, ..., xn) за k крокiв" алгоритмiчно розв’язнi. Прикладами алгоритмiчно нерозв’язних проблем є проблема зупинки і проблема самозастосовностi.
2. Проблема зупинки та самозастосовності, їх нерозв’язність. Наслідки нерозв’язності
Проблема зупинки формулюється так: за x та y установити, чи є визначеним значення x(y).
Проблема самозастосовностi формулюється так: за x встановити, чи є визначеним значення x(x).
Неформально проблема зупинки означає: встановити за x та y, чи спиниться МНР-програма з кодом x при роботi над y. Проблема самозастосовностi неформально означає: встановити за x, чи спиниться МНР-програма з кодом x при роботi над власним кодом.
Предикат "x(y) визначене" позначимо Q(x, y). Предикат "x(x) визначене" позначимо S(x). Зрозумiло, що S(x) Q(x, х).
Тeорeма 1. Проблема самозастосовностi алгоритмiчно нерозв’язна.
Покажемо, що S(x) нерекурсивний. Припустимо супротивне, тодi функція
S(x)
=
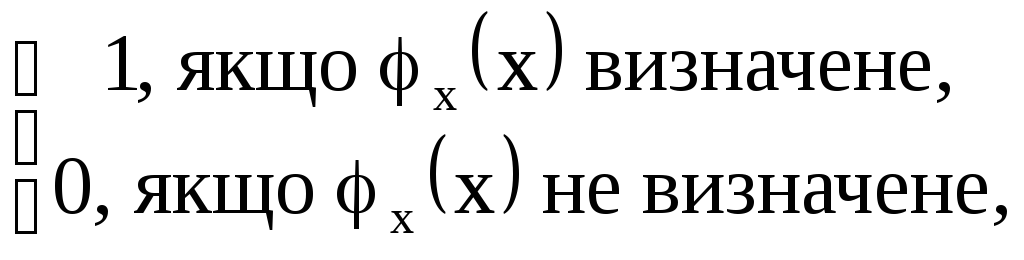є рекурсивною.
Задамо
функцію f(x)
=
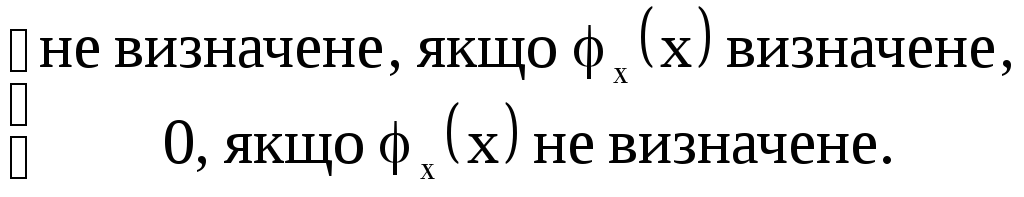
Функцiя f алгоритмiчно обчислювана, тому за ТЧ вона ЧРФ. Нехай n iндекс функцiї f у нумерацiї 1-арних ЧРФ, тобто f(x) – суть n(x). Маємо
n(п)
=
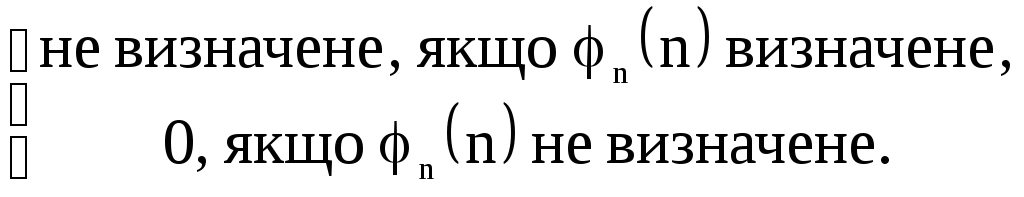
Отримали суперечнiсть!
Наслідок. Проблема зупинки алгоритмiчно нерозв’язна.
Справдi, алгоритмiчна розв’язнiсть проблеми зупинки означає, що предикат Q(x, y) є рекурсивним, звiдки предикат S(x) рекурсивний. Це суперечить теоремi 1.
Тeорeма 2. Проблеми зупинки та самозастосовностi частково розв’язнi.
Для
доведення часткової рекурсивностi
предиката Q(x,
y)
задамо алгоритм обчислення
:
за x
як за кодом МНР-програми вiдновимо Px
i почнемо обчислення Px(y).
Якщо Px(y),
то алгоритм видає 1 як результат; якщо
Px(y),
то алгоритм нiколи не видасть результату,
тобто значення
(x,
y)
тодi не визначене. За ТЧ
є ЧРФ, тому Q є ЧРП. Але
(x)=
(x,
х),
тому S
теж ЧРП.
Тeорeма 3. Множина D = {x | x(x) визначене} нерекурсивна РПМ.
Характеристична функцiя множини D є характеристичною функцiєю предиката S, яка нерекурсивна згiдно з теоремою 1. Множина D є областю визначення ЧРФ u(x)=x(x), тому D є РПМ .
Наслідок
1. Множина
=
{x
| x(x)
не визначене}
не є РПМ.
Припустимо
супротивне:
є РПМ. Тодi
за теоремою Поста множини
та D
рекурсивнi, що суперечить теоремi 3.
Наслідок 2. Предикат S(x) не є ЧРП.
Справдi,
областю iстинностi предиката S
є множина
.
Наслідок 3. Клас РПМ не замкнений вiдносно операцiї доповнення.
Наслідок 4. Клас ЧРП не замкнений вiдносно логiчної операцiї .
На основi отриманих результатiв дiстаємо такi спiввiдношення для вiдповiдних класiв функцiй, множин та предикатiв (тут СМ позначає клас скiнченних множин):
Тeорeма 4. Мають мiсце наступнi строгi включення:
ПРФРФЧРФ; СМПРМРМРПМ; ПРП РП ЧРП.
Функцiя g називається розширенням функцiї f, якщо Df Dg та для всiх xDf маємо f(x) =g(x). Функцiю f тодi називають звуженням функцiї g. Цей факт позначатимемо fg.
Тотальне розширення функцiї називається довизначенням цiєї функцiї.
Рекурсивнi функцiї є тотальними ЧРФ, тому виникає питання, чи можна так довизначити кожну ЧРФ, щоб вона стала рекурсивною.
Тeорeма 5. Функцiя x(x) не має рекурсивних довизначень.
Припустимо супротивне: x(x) має рекурсивне довизначення f(x). Тодi функцiя nsg(x(x)) має рекурсивне довизначення g(x). Нехай k iндекс функцiї g у нумерацiї 1-арних ЧРФ, тобто g – суть функцiя k. Тодi значення k(k)=g(k) визначене, бо g є РФ. Тому значення nsg(k(k)) визначене. Маємо nsg(k(k))=g(k)= k(k) суперечнiсть.
Покажемо, що операцiя мiнiмiзацiї у iстотно вiдрiзняється вiд неконструктивної, взагалi кажучи, операцiї miny для знаходження найменшого значення у, яке задовольняє певну умову.
Функцiя f(x1, ..., xn) виникає iз функцiї g(x1, ..., xn, y) за допомогою операцiї miny, якщо для всiх значень x1, ..., xn
f(x1,...,xn)=
Тeорeма 6. Існує ЧРФ така, що функцiя f(x)=miny((x,y)=0) не є ЧРФ.
Функцiя
(x,y)
=
є ЧРФ за ТЧ.
Функцiя f(x)=miny((x,y)=0) тотальна, бо для всіх xN маємо f(x)=1 або f(x)=0. Якщо xD, то (x,0)=0, тому f(x)=0. Якщо xD, то (x,0) не визначене, але (x,1)=1, тому f(x)=1. Таким чином, f(x)=nsg(D(x)), але тодi f(x) не є РФ i не є ЧРФ.
ЛЕКЦІЯ 14
ПЛАН
-
Нумеровані сукупності ЧРФ. Теорема Райса та її значення.
-
Теорема Райса − Шапіро.