2.4. Основне рiвняння динаміки обертального руху абсолютно твердого тiла

Розглянемо обертання АТТ навколо нерухомої точки О (нехай вона збiгається з центром мас) пiд дiєю зовнiшнiх сил . Вiдповідно до виразу (2.39) його момент iмпульсу

Продиференціюємо за часом цей вираз:

Оскiльки вектори та , колiнеарнi, їх векторний добуток дорiвнює нулю. Тодi з урахуванням формули (2.13) останнiй вираз стане:

де — головний момент зовнiшнiх сил, що дiють на АТТ.

Остаточний вираз має вигляд:

(2.42)

i називається основним рiвнянням динамiки обертального руху АТТ вiдносно нерухомої точки О.

Воно свiдчить про те, що похiдна моменту iмпульсу АТТ за часом дорiвнює головному моменту дiючих зовнiшнiх сил. (Моменти і визначаються вiдносно однiєї й тiєї ж точки обертання О). Якщо АТТ обертається навколо нерухомої осi, то рiвняння (2.42) запишеться у вiдповiдних проекцiях i на цю вiсь:

(2.43)

тобто похiдна за часом вiд моменту iмпульсу АТТ вiдносно нерухомої осi обертання дорiвнює головному моменту зовнiшнiх сил вiдносно цiєї осi.

Рiвняння (2.43) можна записати iнакше, якщо врахувати вирази (2.41) та (1.50), а також те, що момент iнерцiї I = соnst:

тобто

(2.44)

для обертання навколо нерухомої, осi.

Якщо тiло обертається навколо нерухомої точки О, останнiй вираз буде таким:

(2.45)

Цi вирази читаються так: добуток моменту iнерцiї АТТ вiдносно нерухомої точки (або осi) обертання на кутове прискорення дорiвнює головному моменту зовнiшнiх сил вiдносно тiєї ж точки (або осi) обертання.

Неважко побачити, що рiвняння (2.42) i (2.45) нагадують записи другого закону Ньютона для поступального руку (див. рiвняння (2.13) та (2.8)). Тiльки роль маси тут вiдiграє момент iнерцiї , роль сили — момент сили , роль iмпульсу — момент iмпульсу роль лiнійного прискорення — кутове прискорення . Якщо при поступальному русi причиною змiни руху були дiючi сили , то при обертальному русi причиною змiни обертання є момент дiючих сил , причому чим вiн бiльший, тим швидше змінюється обертання.

2.5. Робота, потужнiсть, коефiцiєнт корисної дії

2.5.1. Робота

Розглянемо матерiальну точку, що рухається довiльною траєкторiєю L пiд дiєю змiнної сили (рис. 2.10).

Розiб’ємо цю траєкторiю на елементарнi перемiщення так, щоб на кожному такому перемiщеннi дiючу силу можна було б вважати постiйною.

Тодi скалярний добуток сили на перемiщення буде називатись елементарною роботою :

, (2.46)

або

(2.47)

де — кут мiж векторами i .

Оскiльки ,тобто є проекцiєю сили на дотичну до траєкторiї в даному мiсцi, то вираз (2.47) можна записати як

(2.48)

При , тобто кут гострий, то ; 0. Вiдповiдну силу часто називають рушійною силою (наприклад, сила тяги лiтака або ракети).

При , тобто коли кут тупий, -0 i вiдповiдно силу називають гальмуючою силою (наприклад, сила тертя чи опору).

Якщо ж кут = то = 0 i вiдповiдна сила роботи не виконує (наприклад, сила тяжiння при горизонтальному русi потягу або доцентрова сила).

Повна робота сили (F) при перемiщеннi з точки 1 в точку 2 буде визначатися сумою елементарних робiт, для обчислення якої слід проiнтегрувати вираз (2.47) або (2.48):

(2.49)

Якщо тiло рухається прямолiнiйно пiд дiєю постiйної сили (тобто F = соnst, соs= соnst), то в цьому частинному випадку, враховуючи, що dr =dS, з виразу (2.49) отримуємо:

тобто

(2.50)

Одиницею роботи в системi СІ є джоуль (Дж). 1Дж=1Нм. Роботу сили можна знайти графiчно, якщо відомо її залежнiсть вiд перемiщення (рис.2.11). Добуток на , (див. рис. 2.11), що визначає елементарну роботу , є площиною прямокутника з основою i висотою . Тодi повна робота, як сума таких прямокутникiв, чисельно дорiвнює всiй площi заштрихованої криволiнiйної трапеції, тобто площi пiд графiком функцiї . Такий пiдхiд часто математично спрощує обчислення роботи.

Для прикладу знайдемо роботу зовнiшньої сили, що розтягує пружину (рис.2.12,а). За третiм законом Ньютона ця сила дорiвнює силi пружностi =, але протилежна їй за напрямком: , тому

(2.51)

Графiк цiєї сили подано на рис. (2.12,б). Робота зовнiшньої сили є додатною i чисельно дорiвнює площi заштрихованого трикутника

Цей же вираз можна одержати з виразу (2.49), пiдставивши вираз (2.51):

(2.52)

Розглянемо роботу у разi обертального руху. Нехай до АТТ прикладено дотичну силу , пiд дiєю якої воно повернулося на малий кут (рис. 2.13). При цьому точка прикладання сили перемiстилася на . Як вiдомо, переміщення можна визначити через радiус R та кут :R. Як видно з рис. 2.13, R= l, де l — плече сили . Тодi вiдповiдно до виразу (2.48.) елементарна робота дорiвнюватиме:

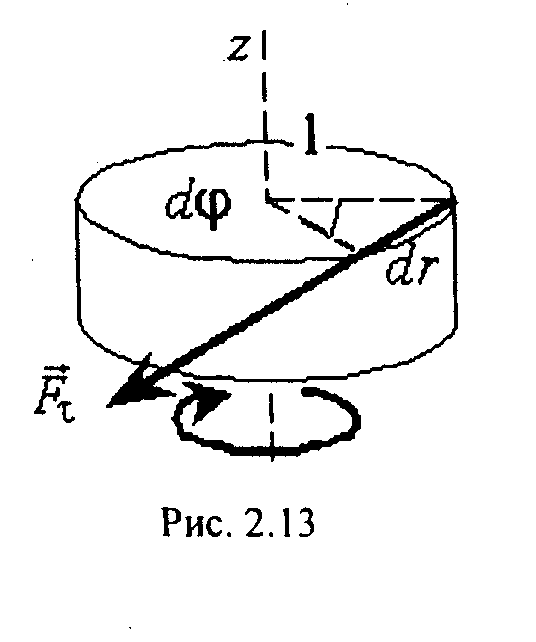
Оскільки F_l=M, то

(2.53)

тобто елементарна робота при поворотi тiла на елементарний кут чисельно дорiвнює добутку моменту дiючої сили на цей кут. Якщо ж тiло повернулося на певний кут вiд положення до положення , то повну роботу в обертальному русi знайдемо шляхом iнтегрування виразу (2.53):

(2.54)

Зокрема, коли момент дiючої сили є постiйною величиною (М=соnst) з виразу (2.54) маємо, що

(2.55)