20.2 Пересечение поверхностей вращения

Частный случай пересечения

Если одна из двух пересекающихся поверхностей является проецирующей, прямолинейные образующие этой поверхности (цилиндра, призмы) перпендикулярны одной из плоскостей проекций, то и проекции линии пересечения на эту плоскость определяется без дополнительных построений.

Н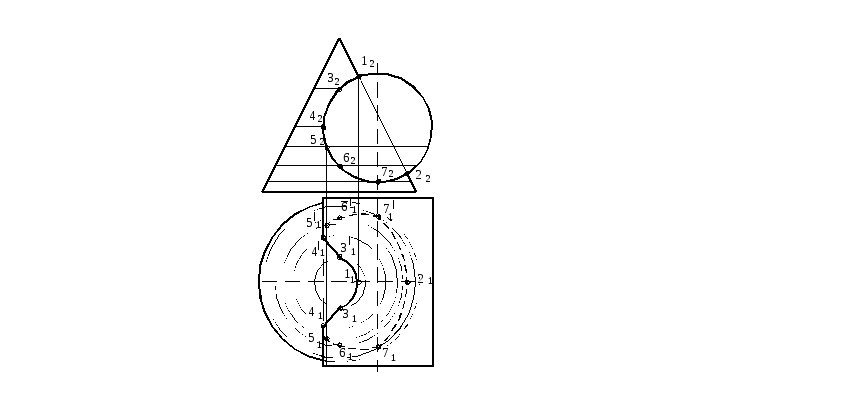а рисунке 124 показано построение линии пересечения конуса вращения с прямым круговым цилиндром.

Фронтальная проекция линии пересечения (проекции точек 1₂,2₂,3₂,4₂,5₂,6₂,7₂) определяется по принадлежности точек поверхности цилиндра. Горизонтальная проекция линии пересечения определяется из условия принадлежности ее поверхности конуса. Для построения горизонтальных проекций точек (1₁,2₂,3₁,4₁,5₁,6_1,7₁), на поверхности конуса проведены параллели через проекции точек, 3₂,4₂,5₂, 6_2, 7_{2 ,} а проекции точек 1₁ и 2₁ определены по принадлежности очерковой образующей конуса.

Рисунок 124

Общий случай пересечения

В общем случае, для построения линии пересечения поверхностей, применяются:

- способ вспомогательных секущих плоскостей, если оси поверхностей не пересекаются;

- способ вспомогательных секущих сфер, если оси поверхностей пересекаются;

Способ вспомогательных секущих плоскостей

Этот способ применяется для построения линии пересечения поверхностей, когда плоскости рассекают пересекающиеся поверхности по графически простым линиям – прямым или окружностям. На рисунок 125 приведен пример построения линии пересечения поверхности конуса с поверхностью сферы этим способом.

Рисунок 125

Конус – прямой круговой и его основание параллельно горизонтальной плоскости проекций. Точки 1 и 5 определяются без дополнительных построений по принадлежности их очерковым образующим обеих поверхностей. Для нахождения проекций точек 3, 3^/ , 2, 2^/ и 4, 4^/ проведены вспомогательные горизонтальные секущие плоскости Р(Р₂), Q(Q₂) и Г(Г₂). Плоскость Р проведена через центр сферы, благодаря чему получены проекции точек 3 и 3^/- характерных точек, определяющих границу видимости линии пересечения на горизонтальной проекции. Секущие плоскости Р, Q и Г рассекают обе поверхности по окружностям радиусов R1, R2 и R3, плоскости которых параллельны горизонтальной плоскости проекций. Горизонтальные проекции точек 3₁, 3^/₁ , 2, 2^/ и 4₁, 4^/₁ определены в точках пересечения соответствующих окружностей. Фронтальные проекции найдены по линиям связи на следах плоскостей Р₂ и Г₂. Полученные точки 1, 2, 3, 4 и 5 последовательно соединены с учетом видимости на каждой проекции.

На рисунок 126 показано определение линии пересечения этих же поверхностей, но со смещением осей вращения относительно фронтальной плоскости проекций на разное расстояние. В этом случае, для определения опорных точек 1 и 5, требуются дополнительные построения. Одним из способов преобразования чертежа приводится положение поверхностей к такому, как показано на рисунок 125. Для этого, через вершины поверхностей проводится вспомогательная секущая плоскость Т (Т₁).

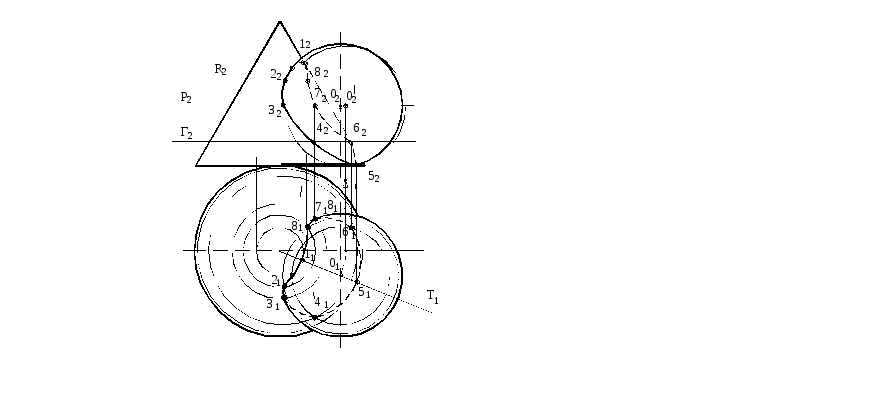
Рисунок 126

Строятся истинные величины сечения (в данном примере методом вращения вокруг оси перпендикулярной П₁ и проходящей через ось вращения конуса) на фронтальной плоскости проекций. Истинная величина сечения конуса плоскостью Т будет треугольник, совпадающий с проекцией самого конуса. Истинная величина сечения сферы плоскостью Т будет окружность, диаметр которой равен диаметру сферы. В пересечении фронтальных проекций сечений конуса с сечением сферы получены фронтальные проекции параллелей опорных точек 1 и 5. Горизонтальные проекции точек 1₁ и 5₁ определятся в пересечении горизонтальных проекций параллелей конуса со следом плоскости Т₁. Фронтальные проекции 1₂ и 2₂ определены по линиям связи на соответствующей параллели конуса. Промежуточные точки 3, 4, 5, 6 построены с помощью горизонтальных секущих плоскостей R(R₂), Р(Р₂) и Г(Г₂). Соединены плавной линией горизонтальные проекции точек 1₁, 2₁, 3₁, 4₁, 5₁, 6_1, 7₁, 8₁ и фронтальные проекции точек 1₂, 2₂, 3₂, 4₂, 5₂, 6₂, 7₂, 8₂ ,учитывая их видимость на поверхностях конуса и сферы. Получена линия пересечения заданных поверхностей. Показана видимость самих поверхностей.

Способ вспомогательных секущих сфер

В ряде случаев в качестве вспомогательных секущих поверхностей, вместо плоскостей, целесообразно применять сферические поверхности (рисунок 127).

Известно, что если центр сферы находится на оси поверхности вращения, то поверхности сферы и тела вращения пересекаются по окружности. И если ось вращения параллельна плоскости проекций, то на эту плоскость полученная окружность проецируется в виде отрезка прямой. Следовательно, если оси двух поверхностей вращения пересекаются и параллельны одной из плоскостей проекций, для определения линии пересечения этих поверхностей можно воспользоваться вспомогательными сферами с центром в точке пересечения осей.

Рисунок 127 Рисунок 128

На рисунке 128 показаны две поверхности вращения (фронтальные проекции): цилиндр и конус, у которых оси пересекаются. Плоскость, образованная пересекающимися осями, параллельна плоскости проекций П₂. Если точку пересечения осей тел вращения принять за центр сферы (шара) и провести сферическую поверхность, пересекающую поверхности цилиндра и конуса то она пересечет их по окружностям, плоскости которых будут фронтально проецирующими плоскостями и на плоскость П₂ проецируются в виде прямых линий, перпендикулярных к осям конуса и цилиндра.

На рисунке 128 линия 1₂-2₂ – фронтальная проекция линии пересечения цилиндра со сферой. Линия 3₂-4₂ – фронтальная проекция линии пересечения конуса со сферой. В пересечении линии 1₂- 2₂ с линией 3₂-4₂ получены точки N и М – точки принадлежащие линии пересечения поверхностей цилиндра и конуса. Аналогично можно построить ряд точек, принадлежащих линии пересечения поверхностей тел вращения, если из точки пересечения осей тел вращения провести ряд концентрических сферических поверхностей, пересекающих оба тела вращения.

Пример. Построить линию пересечения поверхностей цилиндра и конуса, оси которых пересекаются и расположены в общей плоскости симметрии, параллельной плоскости П₂.

На рисунке 129 показано построение проекции линии пересечения этих поверхностей.

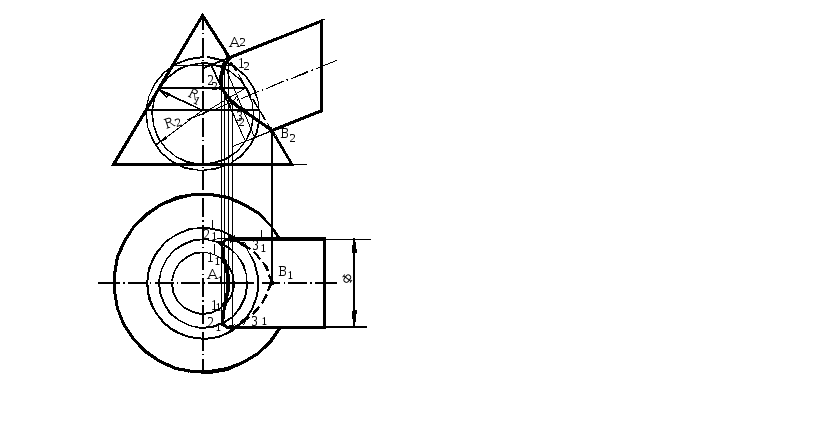
Рисунок 129 Рисунок 130

Из точки пересечения осей проведены две сферы. Сфера минимального радиуса R₁ должна вписаться в одну из поверхностей, а вторую пересечь (касаться очерковых образующих одной поверхности и пересекать крайние образующие второй). Окружности сечений этой сферы с поверхностями цилиндра и конуса проецируются на плоскость П₂ в виде отрезков прямых . Их пересечение определяет положение проекции 2₂ точки, принадлежащей линии пересечения заданных поверхностей. Точки 1 и 3 найдены аналогично, с помощью секущей сферы радиуса R₂. Точки А и В расположены на пересечении очерков заданных поверхностей. Найденные точки А₂, 1₂, 2₂, 3₂ и В₂, соединенные лекальной кривой, являются фронтальной проекцией линии пересечения поверхностей цилиндров.

Если в пересекающиеся поверхности можно вписать общую секущую сферу, То линия их пересечения распадается на две плоские кривые (рисунок 130).

Если у двух пересекающихся поверхностей вращения имеется общая плоскость симметрии, но оси этих тел не пересекаются, то для построения линии их пересечения пользуются способом эксцентрических сфер. Этот способ рекомендуется изучить самостоятельно по указанной литературе.