Определение сил, действующих на заднюю и переднюю стенки методом “тела давления”

Так как плоская стенка является частным случаем стенки криволинейной, то для решения задачи о нахождении силы, действующей на нее, может быть применен метод тела давления.

Основное положение метода “тела давления” – Проекция силы, действующей на стенку на заданное направление, равна проекции полной массовой силы, действующей на “тело давления” в этом же направлении.

Т.к. стенки плоские, то силы направлены по нормали к стенкам, т.е. горизонтально.

Определим проекцию полной силы на горизонтальное направление

.

Тело давления, действующее в горизонтальном направлении, ограничено задней стенкой, горизонталью (дно и его продолжение) и свободной поверхностью (заштрихованный треугольник).

;

т.к. .

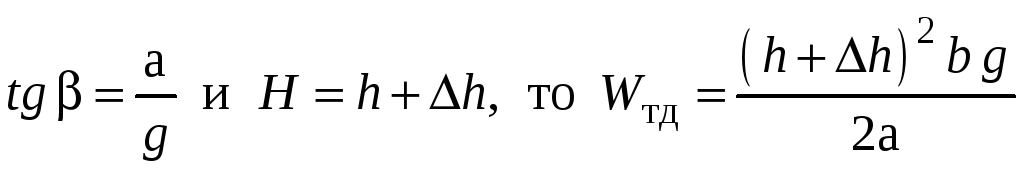Окончательно имеем:

.

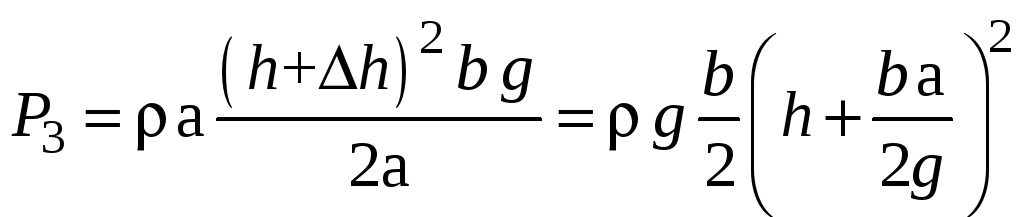Для передней стенки тело давления ограничено стенкой, продолжением дна и продолжением свободной поверхности жидкости и имеет объем ; если , то сила давления на переднюю стенку

;

.

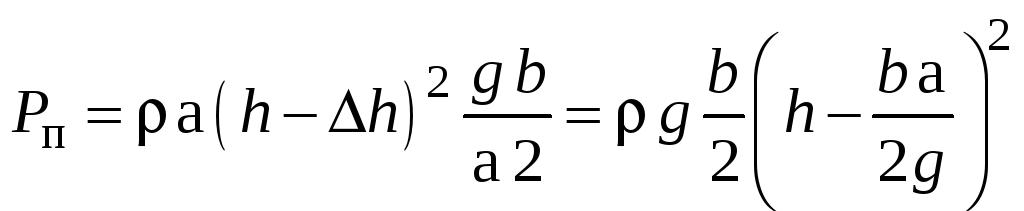Как видим, результаты, полученные различными методами, полностью совпадают. Использовать метод “тела давления” особенно целесообразно при определении силы, действующей на стенку, представляющую комбинацию плоских и криволинейных стенок.

Задача 5.3 Призматический сосуд длиной и шириной , перемещающийся горизонтально с ускорением а, разделен плоской перегородкой на два отсека, заполненных водой до высот .

1. Определить силу давления воды на перегородку.

2. Найти ускорение, при котором эта сила равна нулю.

Д

ано:

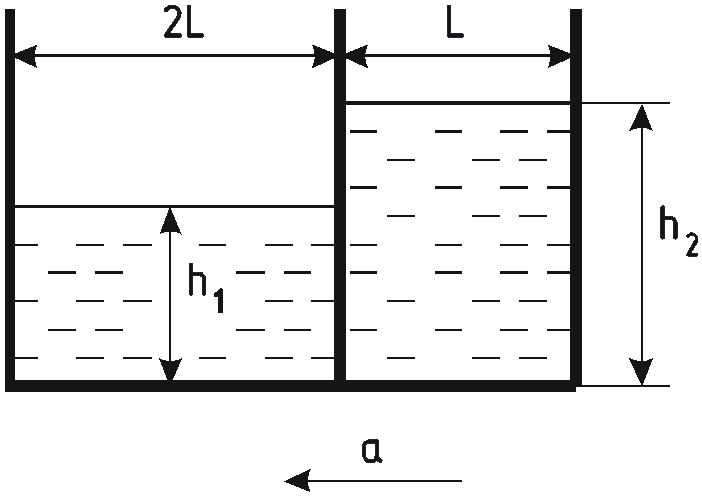
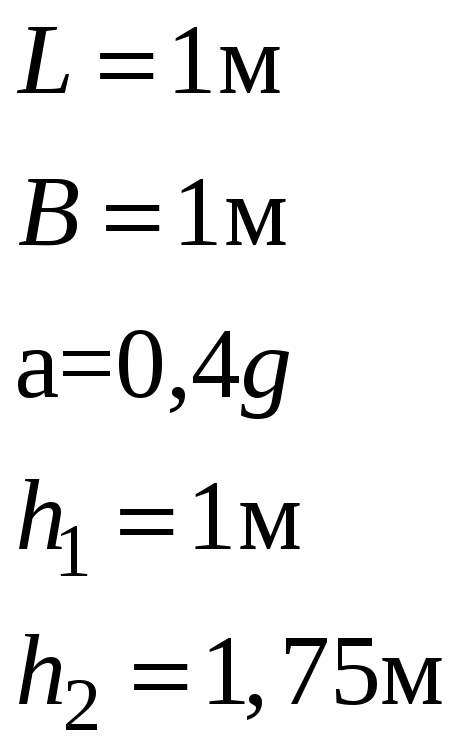
Решение.

1

. При движении с ускорением а свободная поверхность жидкости займет положение, нормальное к направлению действия полной массовой силы.

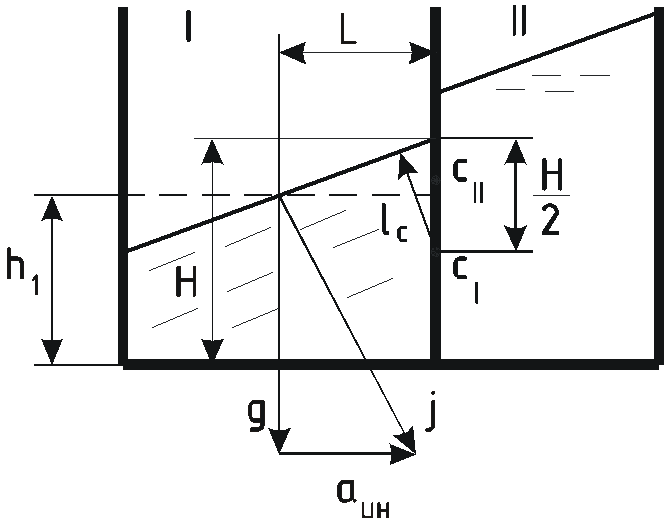
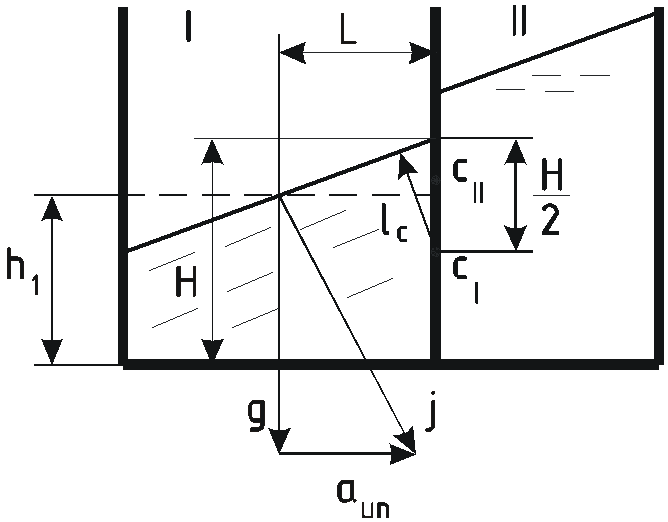
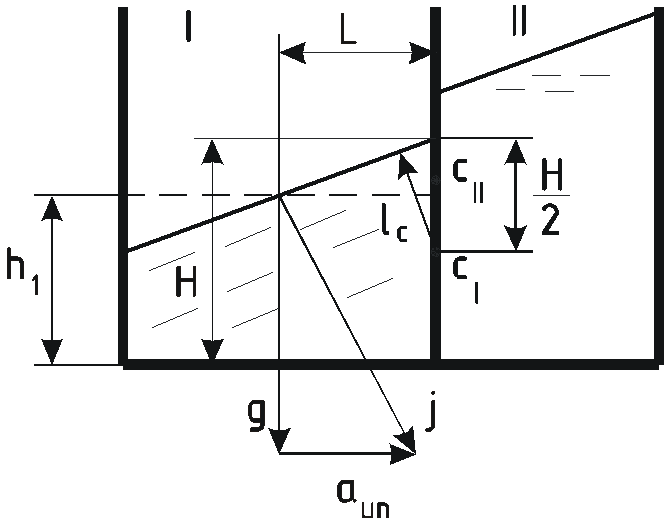
Каждый из отсеков бака сосуда представляет из себя сосуд, силы давления на стенки которого были рассмотрены в задаче 5.2.

Для I отсека перегородка является задней стенкой, а для II отсека – передней.

Полная сила определяется как разность .

О

сновные зависимости:

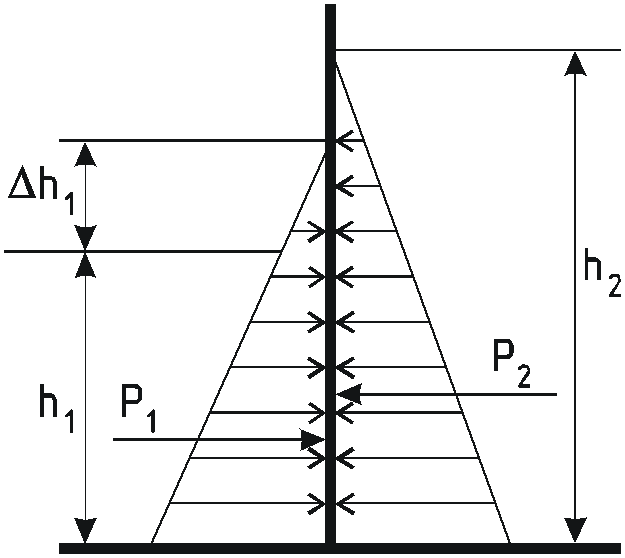
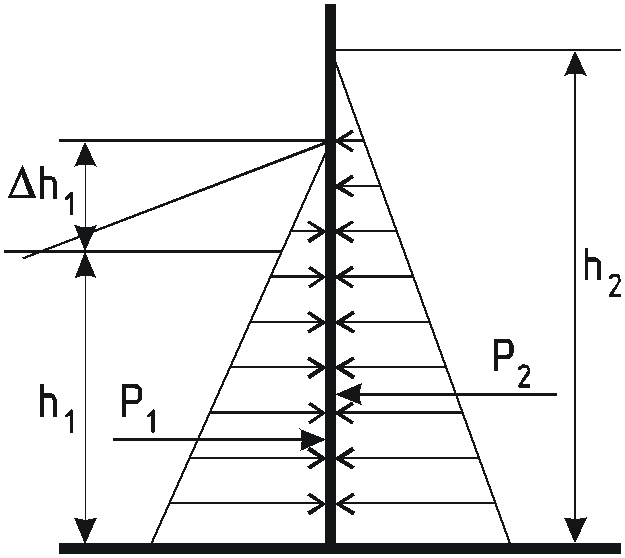
Сила, действующая на плоскую стенку

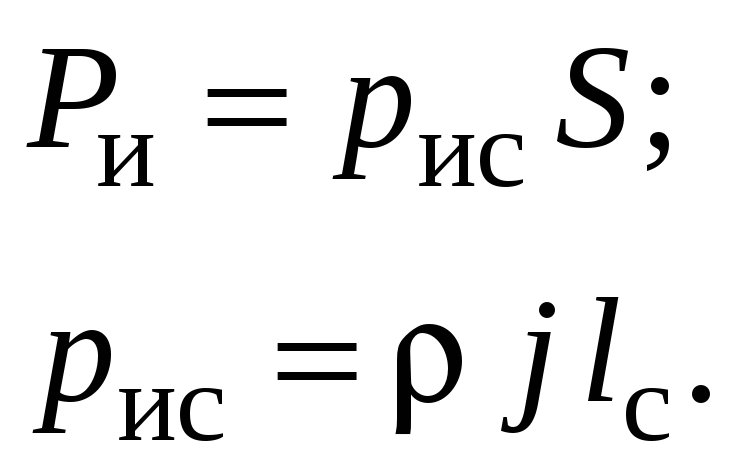
Для отсека I

;

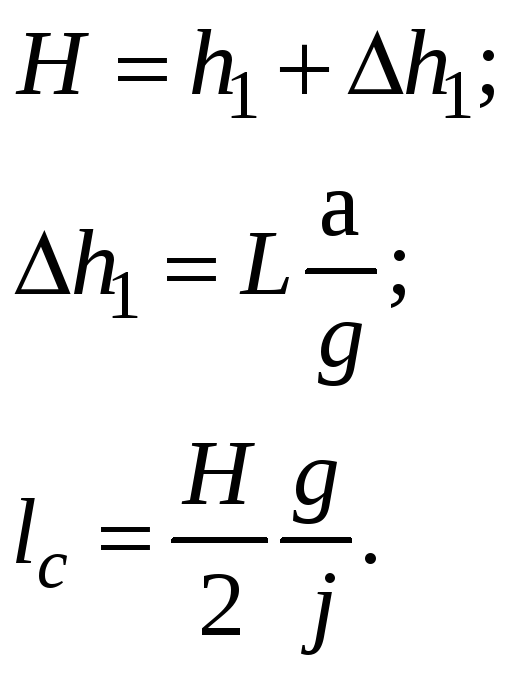
Сила, действующая на перегородку слева – :

.

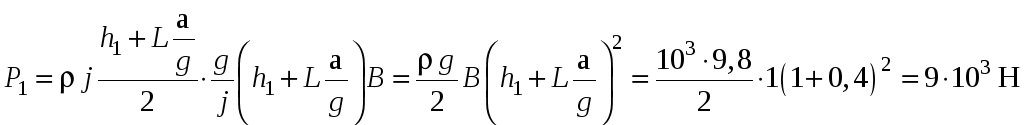Аналогично получаем значение силы, действующей на перегородку со стороны II отсека:

.

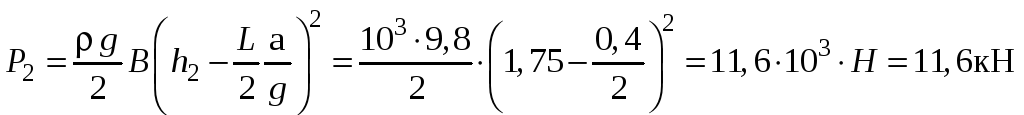Полная сила, действующая на перегородку:

.

2. При условии , сила . Выразив силы через известные величины и ускорение, получим:

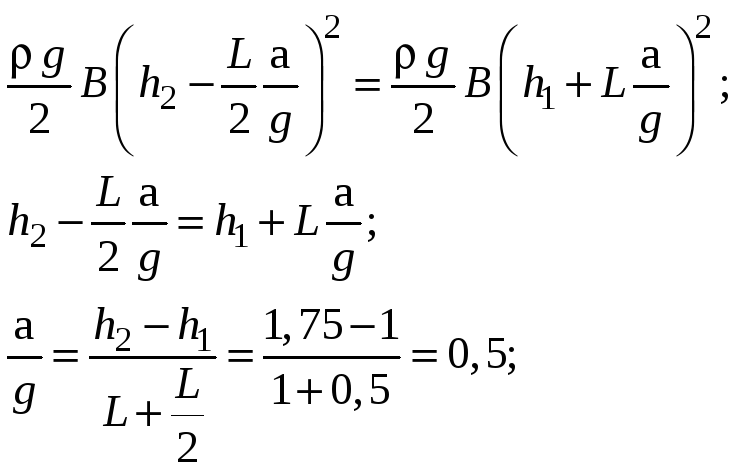
при ускорении сила давления на перегородку равна нулю.

Этот же результат можно было получить графически.

При увеличении ускорения а угол наклона свободной поверхности увеличивается, при этом у перегородки в I отсеке вода поднимается, во втором опускается.

Углы наклона свободной поверхности в обоих отсеках одинаковы, поворот их происходит вокруг центров каждой из поверхностей.

Ч

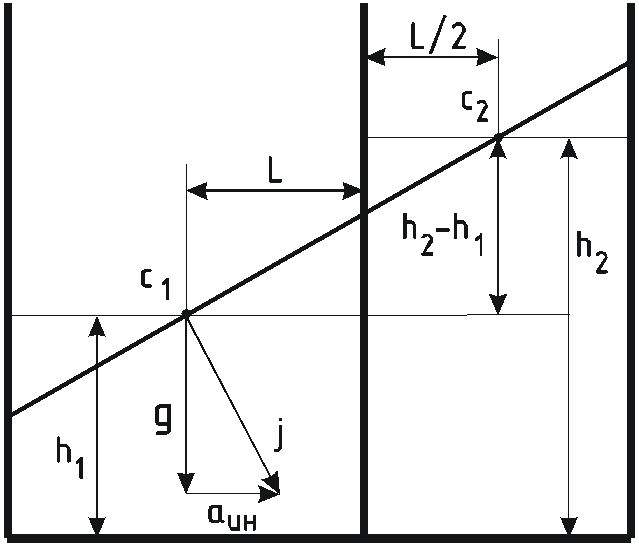
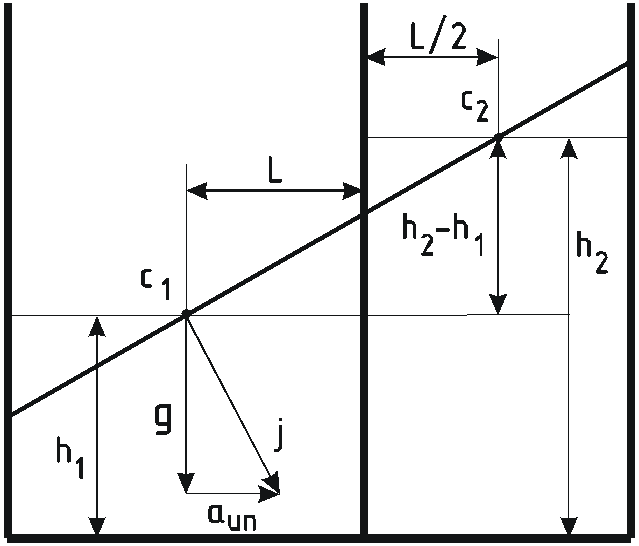
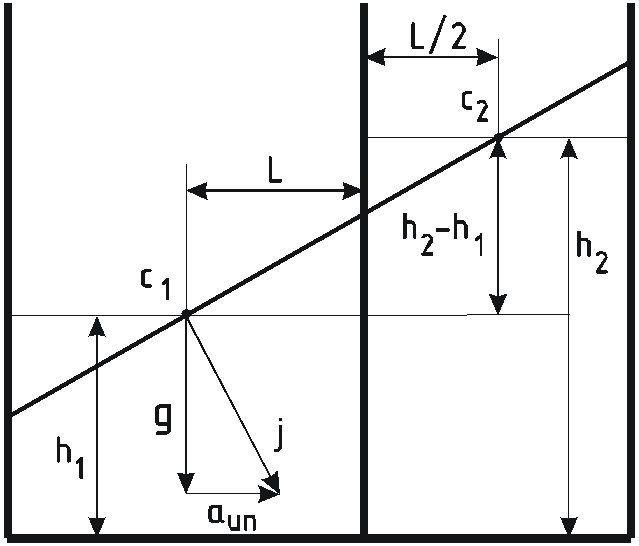
тобы сила, действующая на перегородку, стала равной нулю, необходимо, чтобы точки лежали на одной прямой, нормальной к направлению полной силы .

;

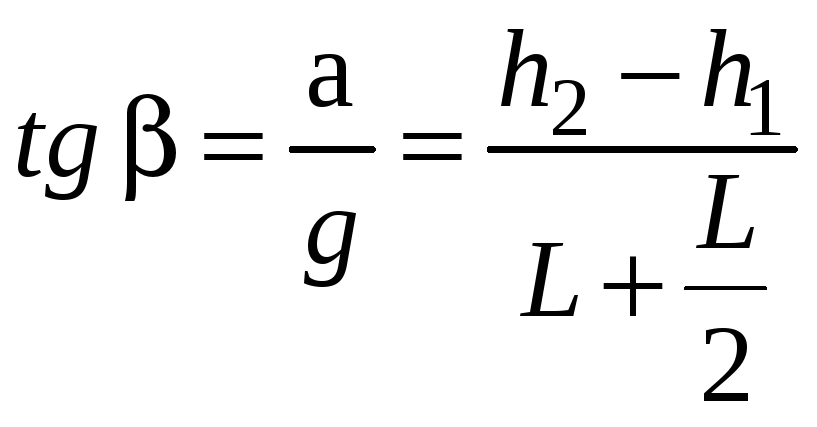откуда ;

.

З

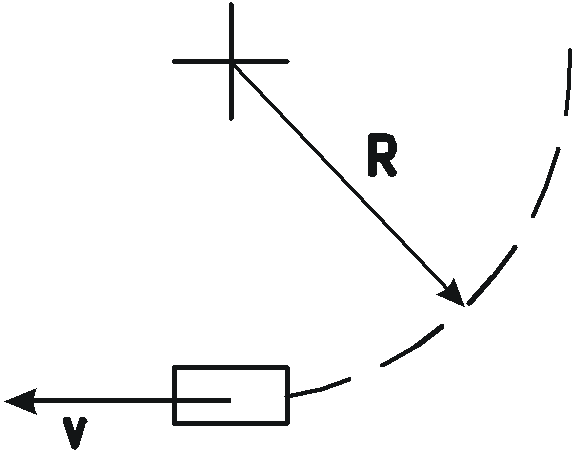
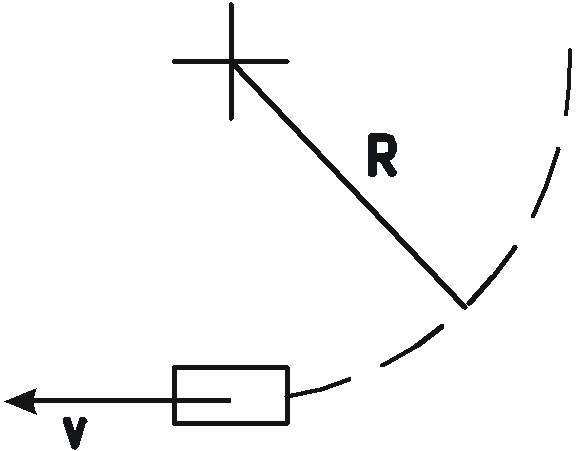
адача 5.4 Определить силу давления бензина на дно самолетного бензобака площадью , заполненного бензином до высоты в момент выхода самолета из пикирования, если радиус кривизны траектории , а скорость .

Дано:

.

Решение.

В момент выхода из пикирования на жидкость в баке действует, кроме силы тяжести, инерционная сила, направленная вертикально вниз.

Результирующая единичная сила .

Полная сила давления жидкости на дно бака (при условии, что дно горизонтально)

Ускорение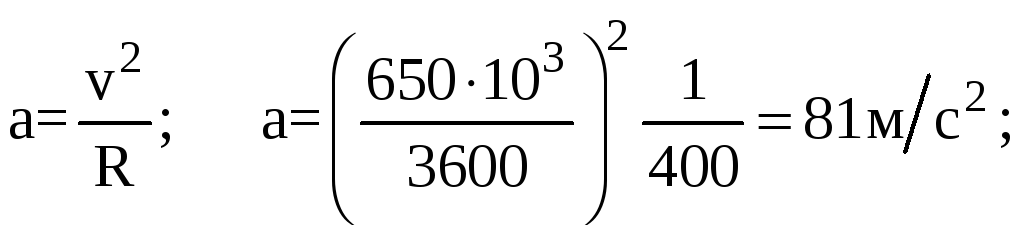

.

Задача 5.5 Длина пробега самолета после посадки со скоростью составила 500 м.

Какая часть объема топлива должна оставаться в баке в момент приземления, чтобы при торможении самолета дно бака не оголилось?

Бак имеет форму параллелепипеда с горизонтальным дном размером и передней стенкой, перпендикулярной направлению движения, высотой .

Движение самолета после посадки считать прямолинейным и равнозамедленным.

Д

ано:

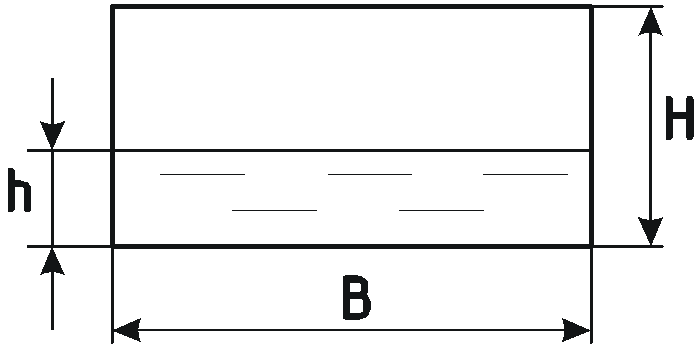
Объем бака ;

.

Найти .

Решение.

При равномерном движении и в состоянии покоя бак был заполнен до высоты , и объем оставшегося в нем топлива составлял:

.

Полный бак имеет объем .

Искомая часть объема составит:

.

При действии постоянного ускорения торможения а свободная поверхность жидкости расположится перпендикулярно действию результирующей массовой силы .

Учитывая, что объем топлива в баке остался неизменным, положение свободной поверхности найдем по координатам точек . В точке жидкость опустилась на глубину до дна, в точке поднялась на ту же высоту , а точка - центр свободной поверхности топлива остался на месте.

У

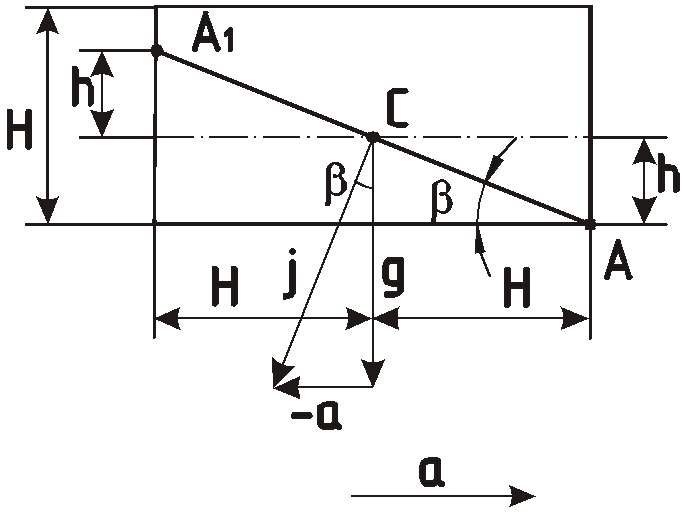
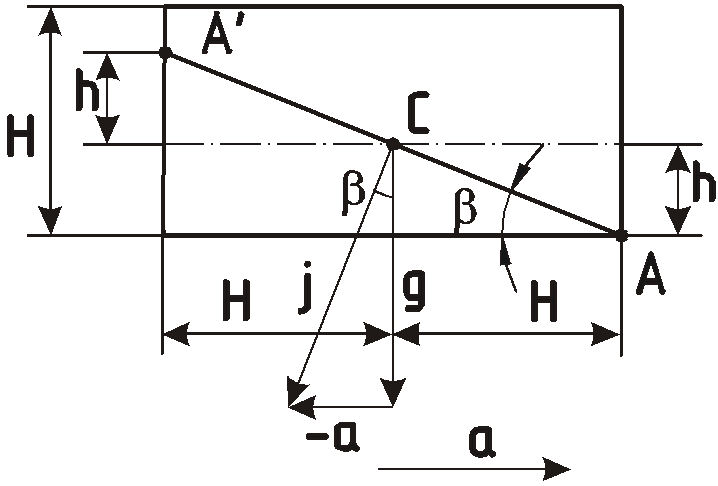
глы равны, как углы между взаимно перпендикулярными прямыми и, следовательно, .

Значение ускорения торможения а находим из , где - длина пробега или тормозной путь

;

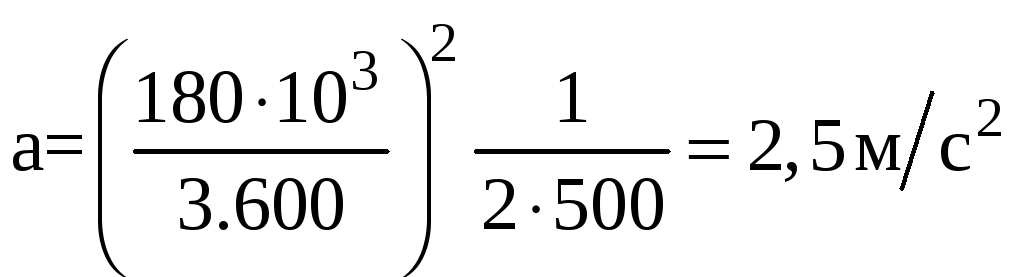окончательно находим:

.

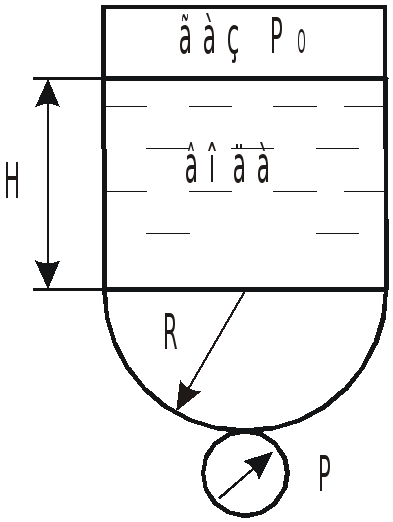
Задача 5.6 Цилиндрический сосуд, заполненный водой, поднимается вверх с ускорением .

1. Определить усилие 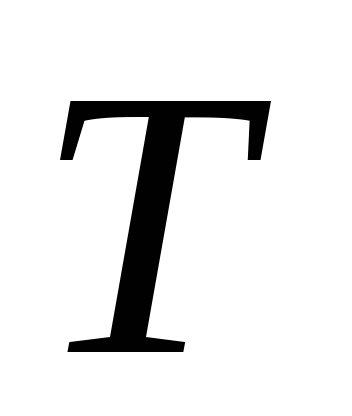в тяге.

2. Построить эпюры давления жидкости по высоте и стенкам сосуда при движении и в неподвижном состоянии.

3. Н

   

   

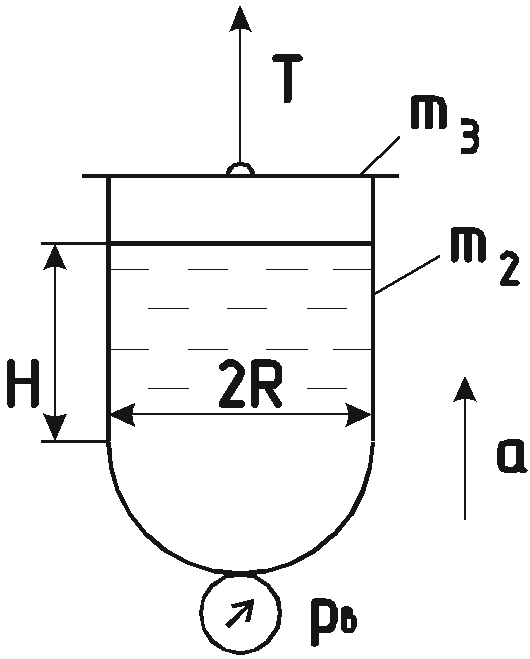
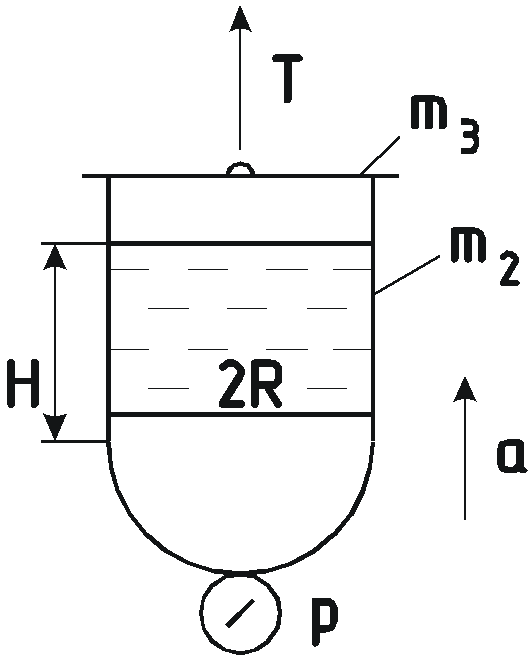
   айти силу давления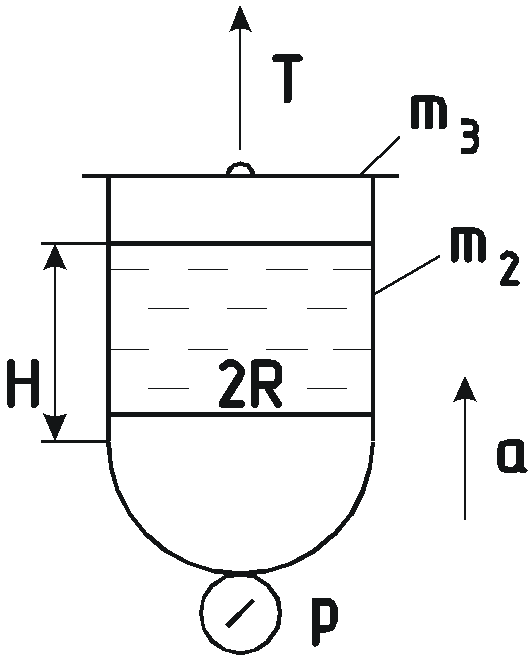 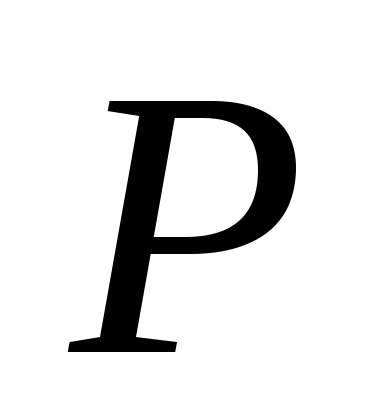на полусферическое дно сосуда, если вакуумметр, присоединенный к нижней точке сосуда показывал 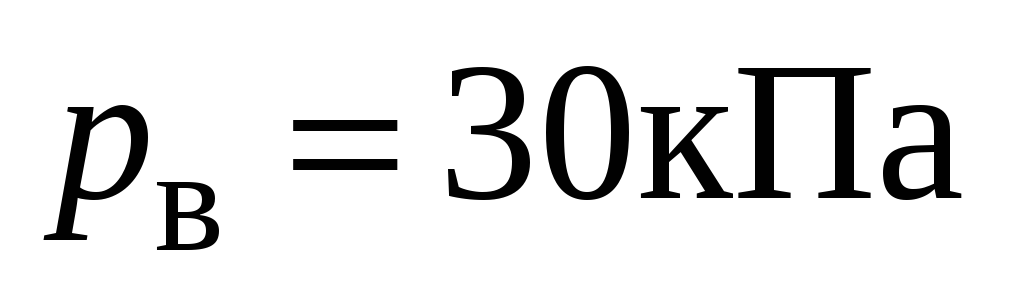, когда сосуд был неподвижен.

Дано:

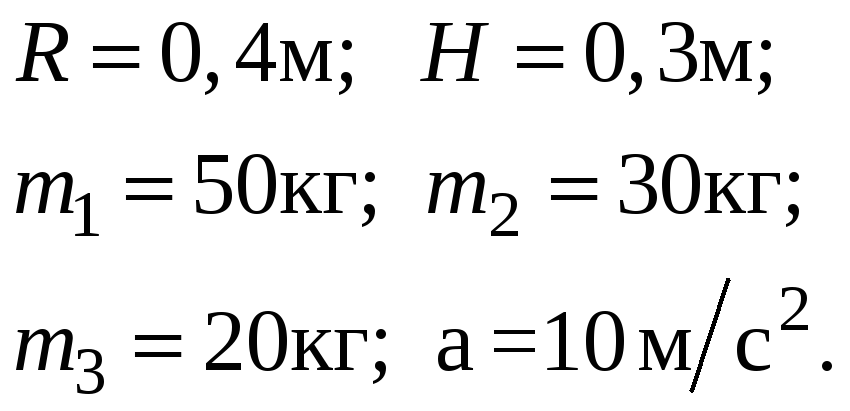
Решение.

1. Определение усилия в тяге .

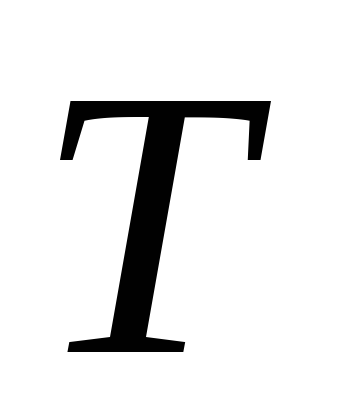, где - масса; - ускорение.

П

ри движении с ускорением а полное ускорение определяется как:

.

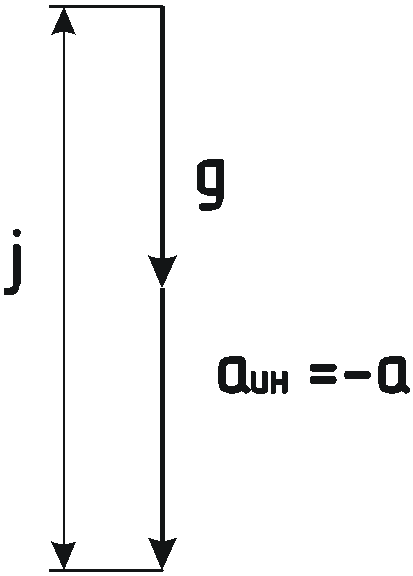
Тогда:

, где

- масса жидкости в сосуде,

;

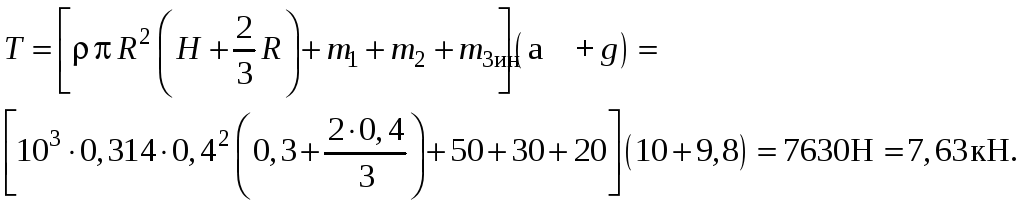
2. Построение эпюр давления.

В неподвижном сосуде давление в жидкости по высоте изменяется по закону:

;

а при движении вверх с ускорением а –

.

У

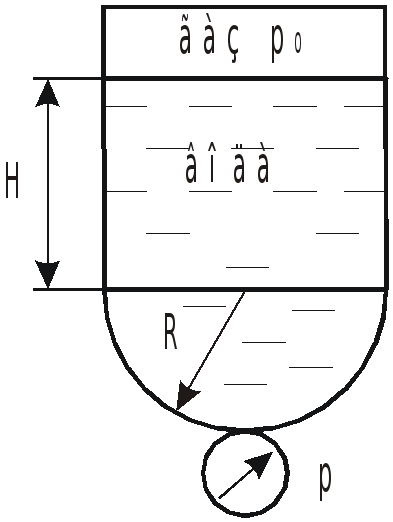
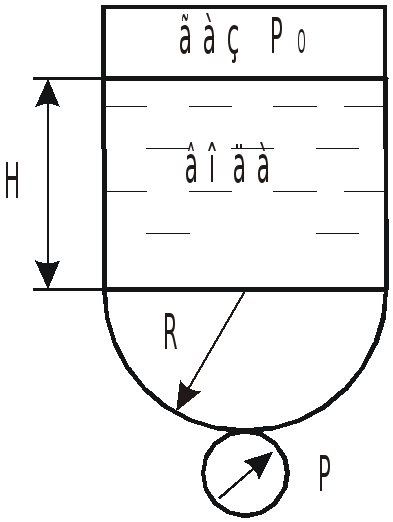
читывая, что плотность газа в верхней части сосуда над свободной поверхностью воды несоизмерима с плотностью воды, считаем, что давление во всех точках газовой полости остается одинаковым в состоянии покоя и при движении с ускорением и определяется по зависимости:

.

В шкале избыточных давлений с учетом того, что

и принимая в состоянии покоя, имеем:

или .

При движении вверх с ускорением а давление в нижней точке определяем в шкале избыточных давлений:

;

.

Строим эпюры давлений.

В состоянии покоя

При движении

с ускорением а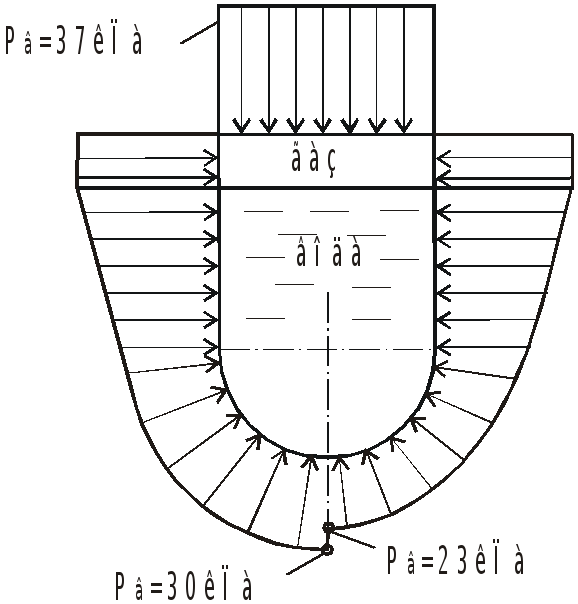

3. Определение силы давления на дно сосуда.

Дно сосуда представляет полусферу, т.е. криволинейную стенку. Полная сила может быть найдена как сумма проекций этой силы на 3 любых взаимноперпендикулярных направления.

В данной задаче, наиболее целесообразно выбрать горизонтальное и вертикальное направления. Ввиду симметричности сосуда все силы, действующие в горизонтальной плоскости, уравновешены.

Вертикальная составляющая силы давления на криволинейную стенку равна весу тела давления:

.

Д

ля нахождения объема тела давления необходимо найти положение поверхности атмосферного давления, т.к. тело давления ограничено этой поверхностью, криволинейной стенкой и вертикальными образующими, проходящими через границы стенки.

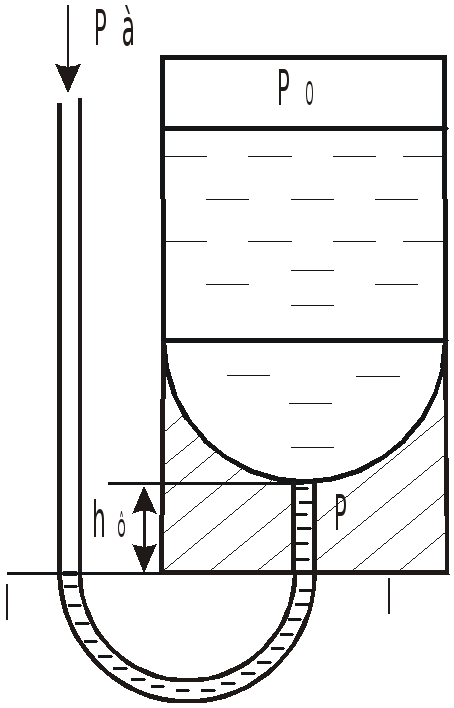
При движении вакуумметр показывал . Если представить его в виде -образной трубки, то вода в свободном колене должна была бы опуститься на и поверхность атмосферного давления заняла бы положение I-I.. Тело давления занимает заштрихованный объем , равный объему цилиндра с высотой за вычетом объема полусферы:

.

Сила, действующая на дно, направлена вверх и определяется как

.

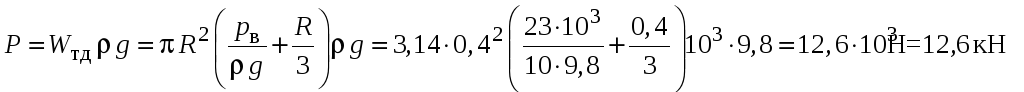Задача 5.7 Определить горизонтальную и вертикальную составляющие силы давления бензина с плотностью на верхнюю полусферическую крышку бака при полете самолета с ускорением , если манометр, установленный в верхней точке показывает .

Как изменятся эти силы при полете с постоянной скоростью?

Р

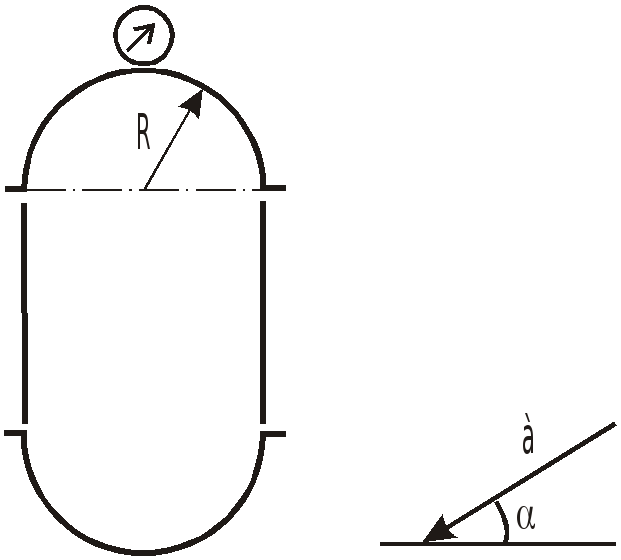
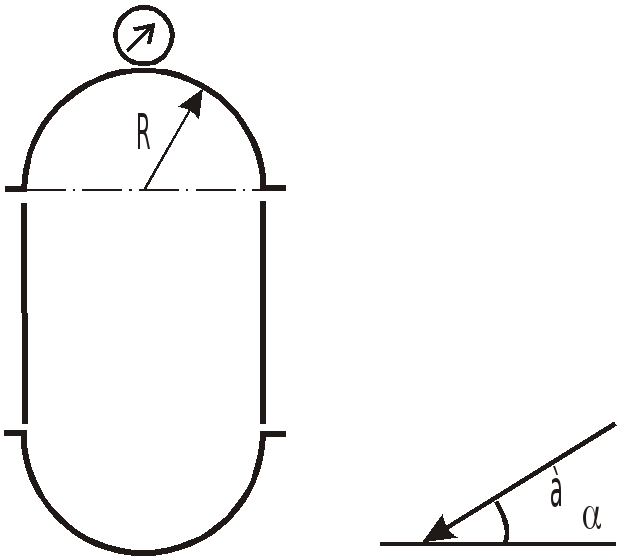
адиус , угол .

Дано:

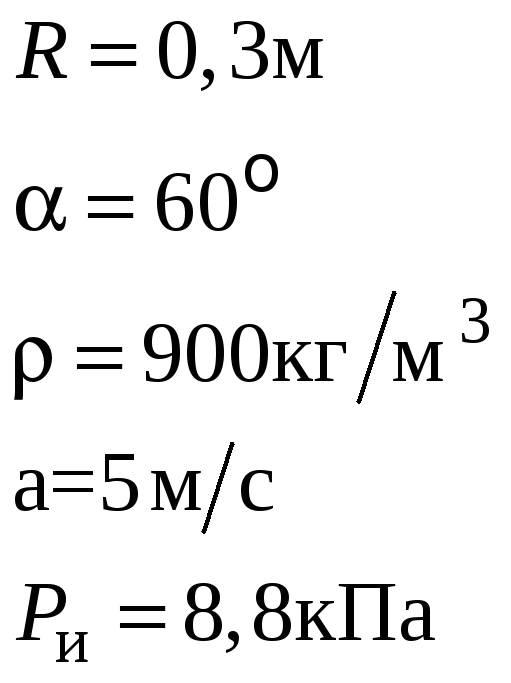
Решение.

1. П

   

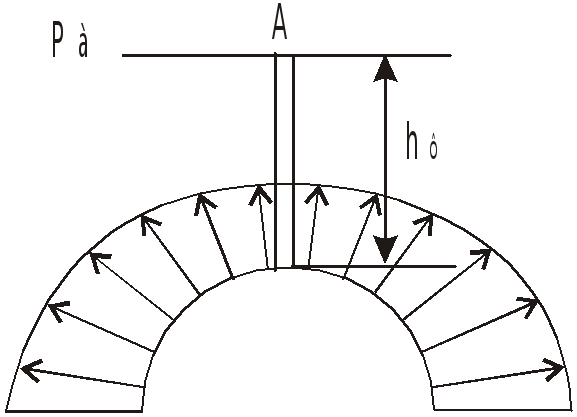
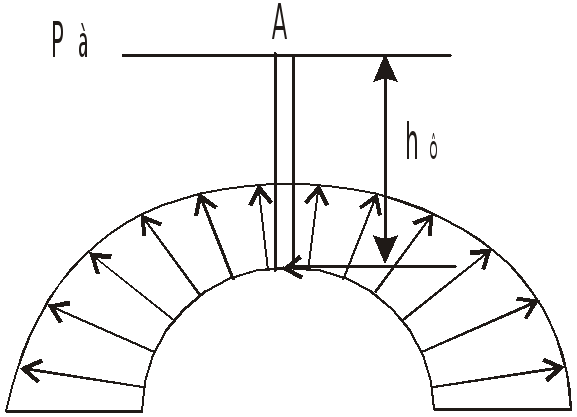
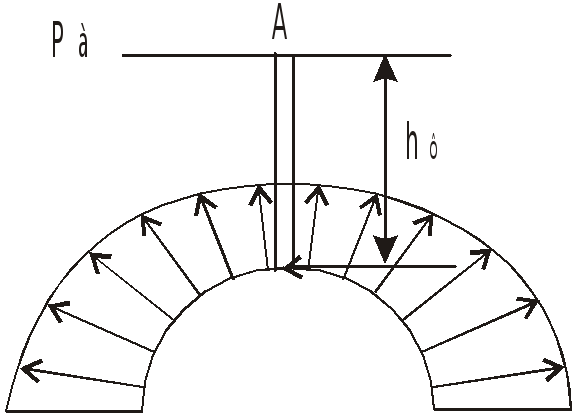
   ри полете с постоянной скоростью единственной массовой силой является сила тяжести. Крышка имеет ось симметрии, поэтому горизонтальные составляющие сил давления взаимно уравновешены и 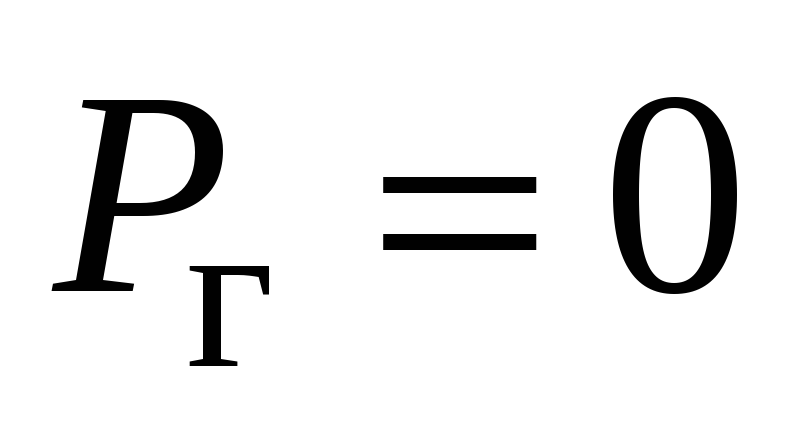, а вертикальная составляющая равна весу тела давления:

.

Д

ля нахождения тела давления надо найти положение поверхности уровня с давлением, равным атмосферному. Если в верхней точке установить пьезометр, то жидкость в нем поднимется на высоту:

.

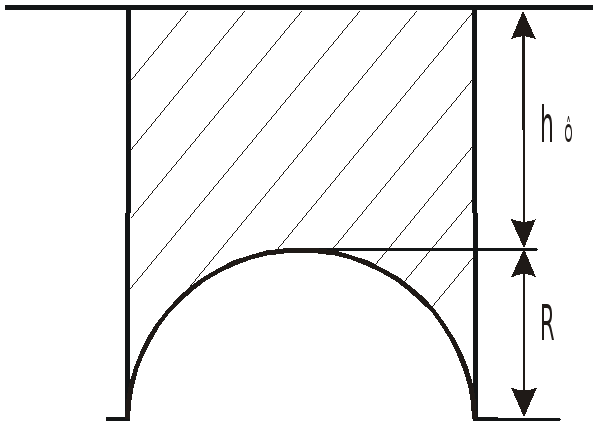
Тело давления имеет объем:

;

.

2. При движении с ускорением а результирующая массовая сила определится сложением силы тяжести и инерционной силы:

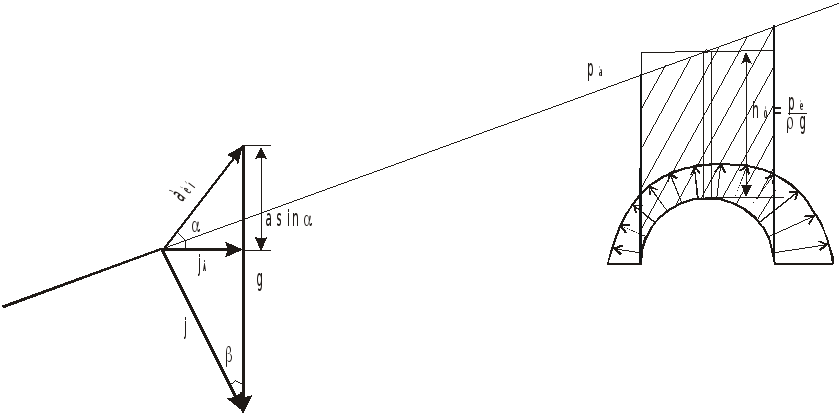
Поверхности уровня должны быть перпендикулярны силе . Поверхность атмосферного давления займет положение, показанное на рисунке.

Вертикальная и горизонтальная проекции полной силы, действующей на крышку, могут быть определены методом “тела давления”.

Определение вертикальной составляющей:

.

Из треугольника сил имеем:

.

Форма тела давления для определения вертикальной составляющей показана на рис.

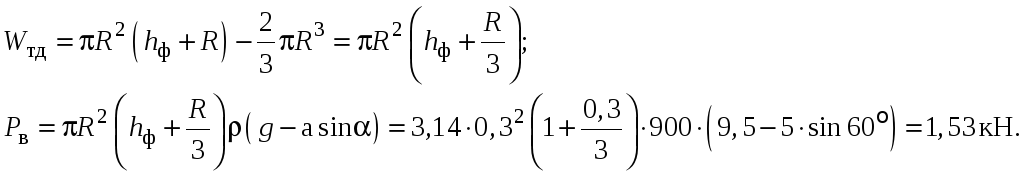
Определение горизонтальной составляющей:

.

Форма тела давления для определения горизонтальной составляющей показана на рис. Из треугольника сил имеем:

.

При движении с ускорением, направленным вниз под углом , вертикальная составляющая полной силы, действующей на крышку, уменьшилась по сравнению с покоем или равномерным прямолинейным движением, и появилась горизонтальная составляющая, величина которой не зависит от величины избыточного давления в баке, а зависит только от горизонтальной составляющей ускорения.

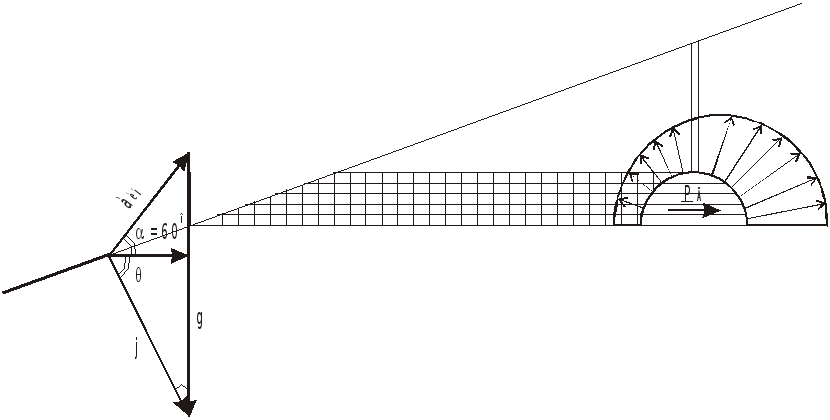
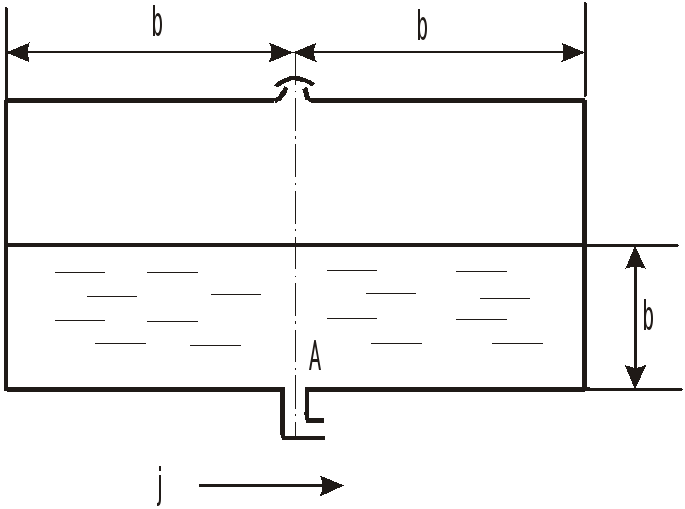
Задача 5.8

Сосуд с размерами разделен пополам вертикальной перегородкой () с отверстием в нижней части.

1. О

   

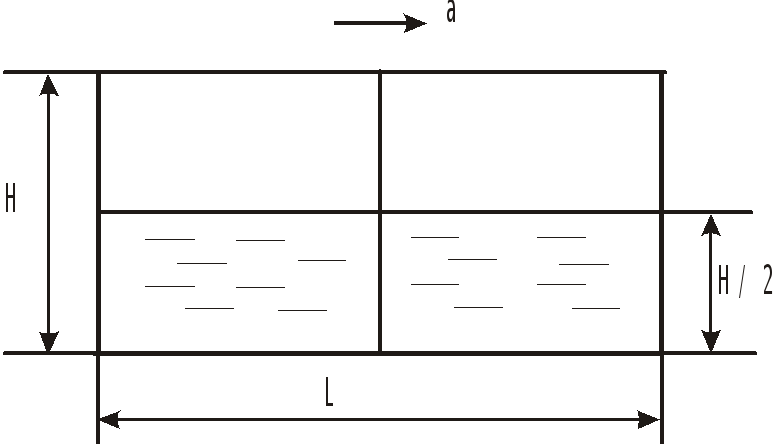
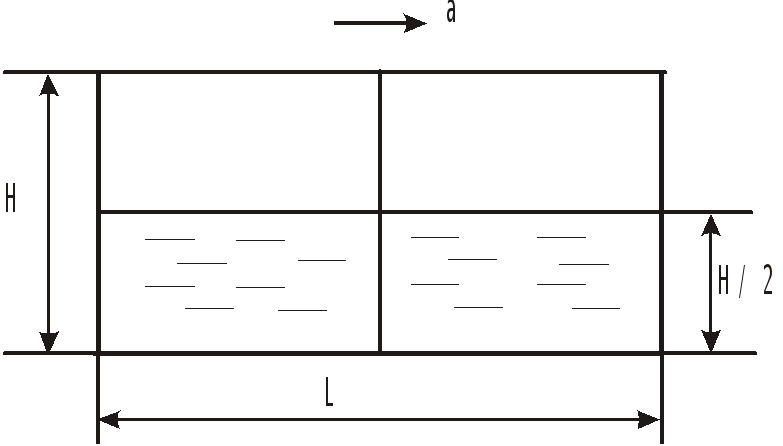
   пределить минимальное горизонтальное ускорение а, при котором вода начнет выливаться из бака. При этом ускорении определить силу давления на перегородку 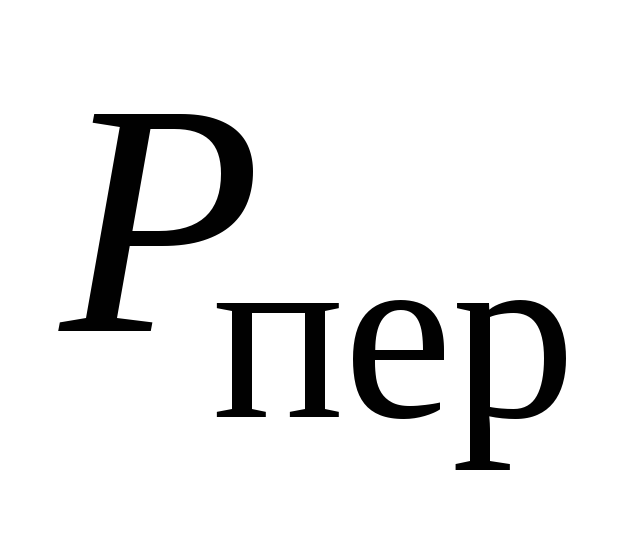и на переднюю 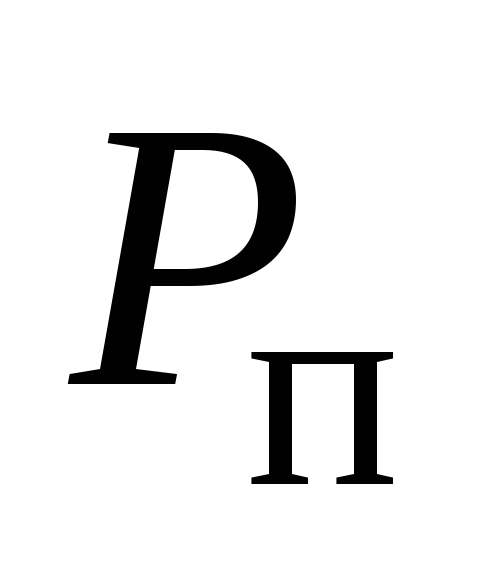и заднюю 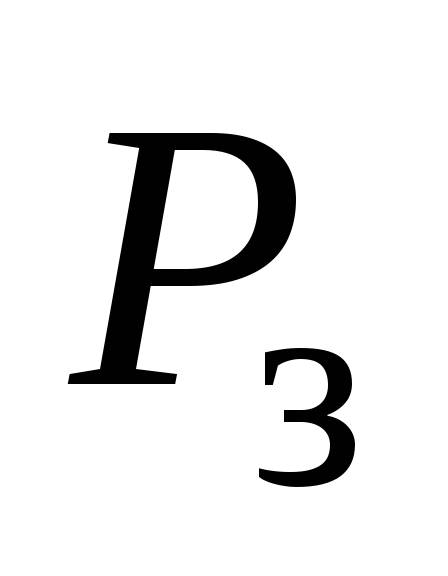стенки () .

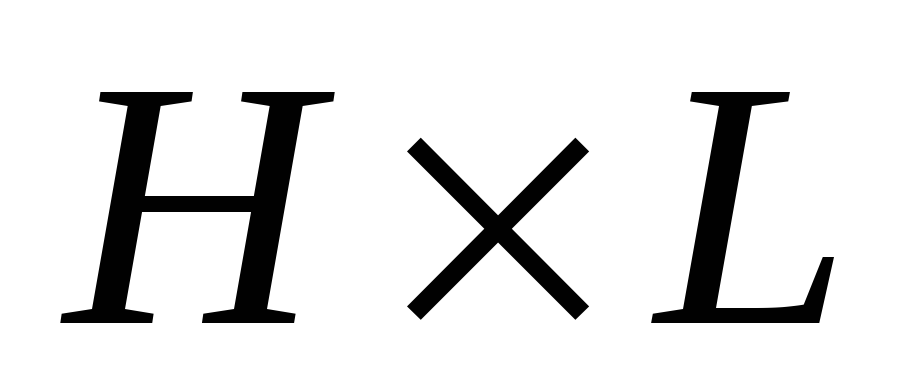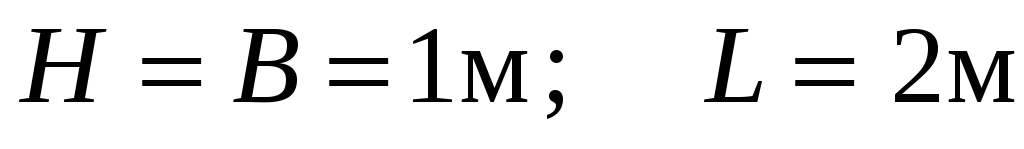2. Ответить на эти же вопросы при условии, что отверстие в перегородке отсутствует.

Ответ.

1) ;

2) .

З

адача 5.9

Топливный бак самолета заполнен на 1/3 его емкости. Самолет движется горизонтально с постоянным ускорением а. Определить значения ускорения, при которых свободная поверхность

1. достигает дна бака;

2. проходит через точку А, что будет соответствовать прекращению подачи бензина из бака.

О

твет: .

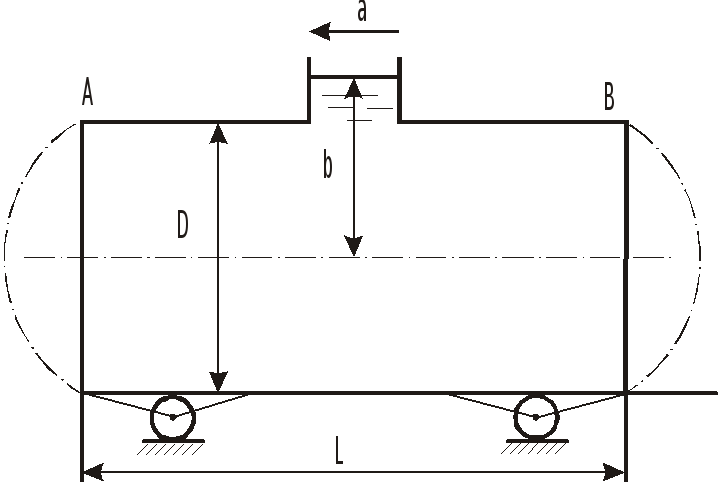
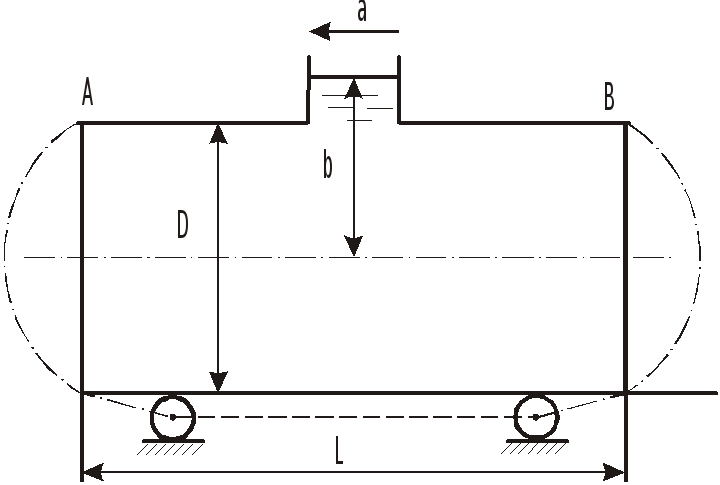
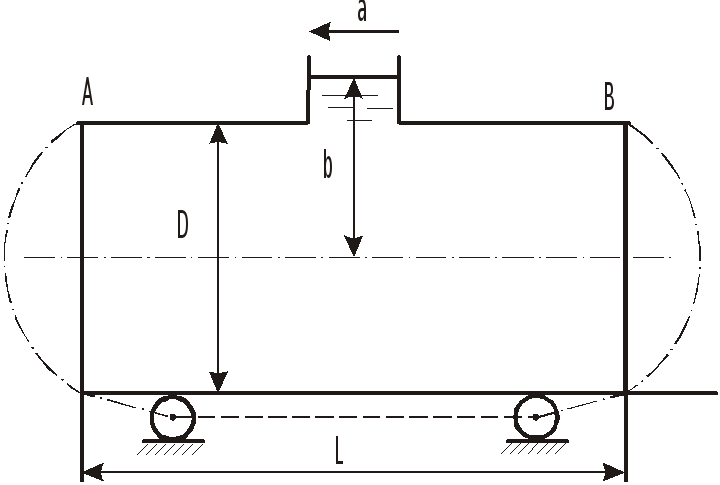
Задача 5.10

Цистерна диаметром и длиной , наполненная нефтью (относительная плотность ) до высоты движется горизонтально с постоянным ускорением .

1. Определить силы давления на плоские боковые крышки.

2. Как изменятся эти силы при замене плоских крышек сферическими?

Увеличение объема цистерны при такой замене равно , где .

Ответ:

З

адача 5.11

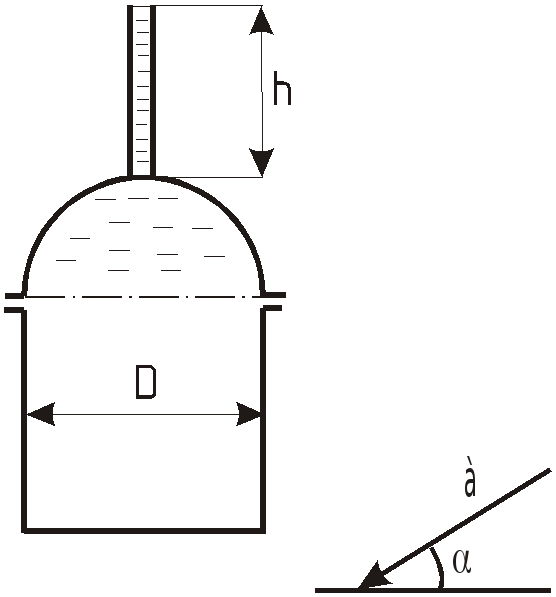
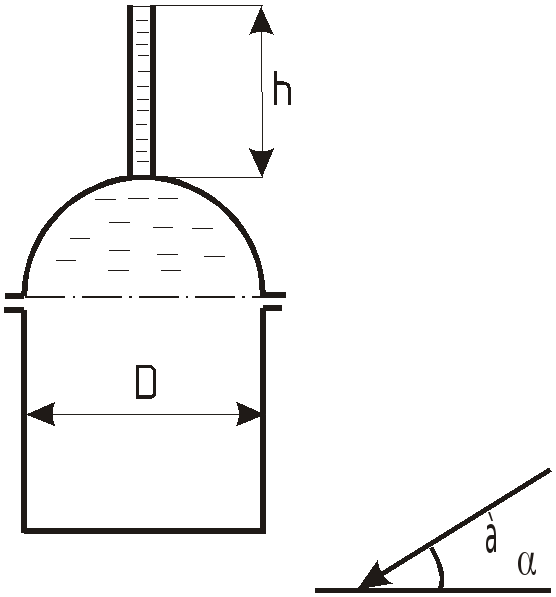
Определить горизонтальную и вертикальную составляющие силы давления на полусферическую крышку цилиндрического сосуда диаметром , движущегося с ускорением под углом к горизонту , если сосуд заполнен водой до уровня в открытой трубке, присоединенной к верхней его точке.

Ответ: ;

для неподвижного сосуда .