- •Раздел 1. Свойства жидкости
- •Свойства давления.
- •Раздел 2. Закон распределения давления в жидкости
- •Раздел 3. Сила давления жидкости на плоскую стенку
- •З адача 3.2
- •Раздел 4. Сила давления на криволинейную стенку
- •Задача 4.4
- •Раздел 5. Относительное равновесие жидкости в сосудах, движущихся прямолинейно с постоянным ускорением
- •Определение сил, действующих на заднюю и переднюю стенки методом “тела давления”
- •Раздел 6. Относительное равновесие жидкости во вращающихся сосудах Равномерное вращение цилиндрического сосуда вокруг вертикальной оси.
- •Равномерное вращение цилиндрического сосуда вокруг оси, не совпадающей с вертикалью.
- •Раздел 7. Уравнение бернулли для потока идеальной жидкости
- •Раздел 8. Уравнение бернулли для потока реальной жидкости.
- •Раздел 9. Течение жидкости в каналах некруглого поперечного сечения.
- •Раздел 10. Истечение жидкости через отверстия и насадки
- •Истечение через отверстия
- •И стечение через насадки
- •Определение коэффициентов истечения опытным путем.
- •Раздел 11. Гидравлический расчет трубопроводов Простой трубопровод.
- •Последовательное соединение трубопроводов.
- •Параллельное соединение трубопроводов.
- •Расчет сложного трубопровода.
- •1 Приближение
- •2 Приближение
З адача 3.2
Определить силу избыточного давления
бензина, действующую на круглую
вертикальную крышку и место ее приложения,
если манометр, расположенный в верхней
точке резервуара показывает
![]() ,
диаметры
,
диаметры
![]() .
Плотность бензина
.
Плотность бензина
![]() .
.
Р


Сила избыточного давления на плоскую
крышку
![]() ,
если
,
если
![]() отсчитывается от поверхности с атмосферным
давлением или
отсчитывается от поверхности с атмосферным
давлением или
![]() - если
- если
![]() отсчитано от поверхности с
отсчитано от поверхности с
![]() .
.
Определим положение поверхности с
![]() .
.
В условии задачи:
![]() .
.
Фиктивная высота ![]() .
.
При определении
![]() можно было воспользоваться внесистемными
единицами:
можно было воспользоваться внесистемными
единицами:
![]() ;
;
![]() ;
;
![]() .
.
![]() .
.
Центр давления
![]() смещен относительно центра масс C на
смещен относительно центра масс C на
![]() ;
;
для круга
![]() .
.
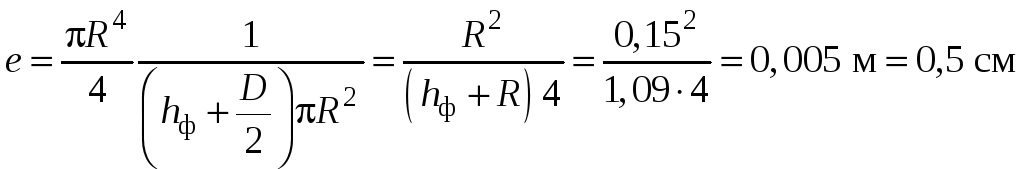 .
.
Ответ: сила
![]() приложена на 0,5 см ниже оси.
приложена на 0,5 см ниже оси.
З
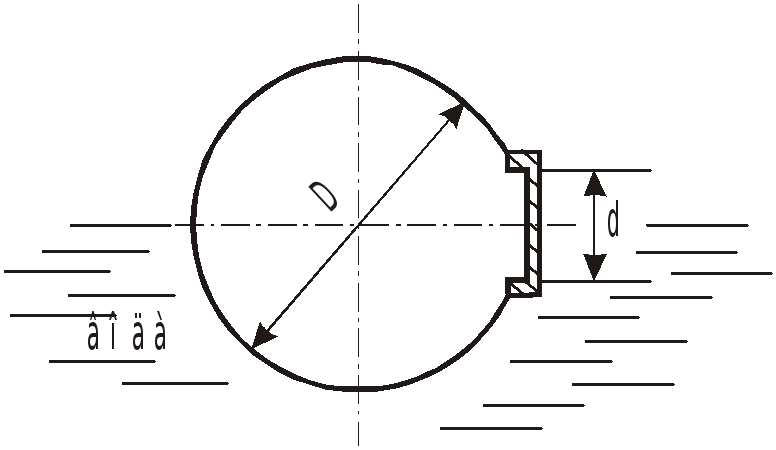
1. Определить силу давления
![]() на крышку, если внутри аппарата вакуум
на крышку, если внутри аппарата вакуум
![]() .
.
2. Найти место приложения этой силы.
Плотность воды
![]() .
.
Диаметр крышки
![]() .
.
Решение:
Эпюра сил давления на крышку имеет вид, показанный на рисунке.
Силы, действующие с обеих сторон крышки, направлены в одну сторону.
Р

![]() ,
,
![]() ,
,
![]() .
.
Положение центра масс для полукруга (см. табл. разд. 3)
![]() ;
;
![]() .
.
Д
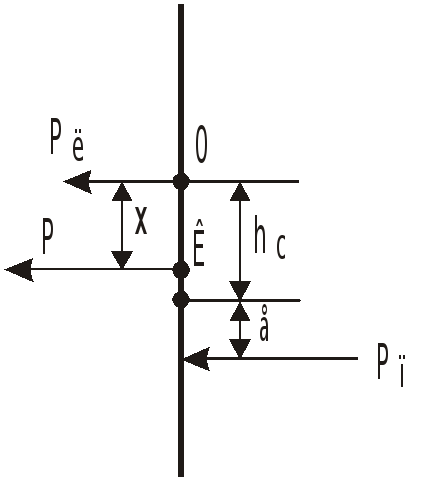

![]() (К – точка приложения результирующей
силы).
(К – точка приложения результирующей
силы).
Обозначим через
![]() расстояние от оси крышки до точки
приложения результирующей силы.
расстояние от оси крышки до точки
приложения результирующей силы.
![]() ,
откуда
,
откуда
![]() .
.
Правая площадка представляет полукруг,
из таблицы находим
![]() ;
;
![]() ;
;
![]() .
.
Ответ:
![]() .
.
З

![]() ,
при котором клапан площадью
,
при котором клапан площадью
![]() будет поддерживать в баке уровень
будет поддерживать в баке уровень
![]() .
.
Ответ: расстояние от верхнего края щитка до шарнира
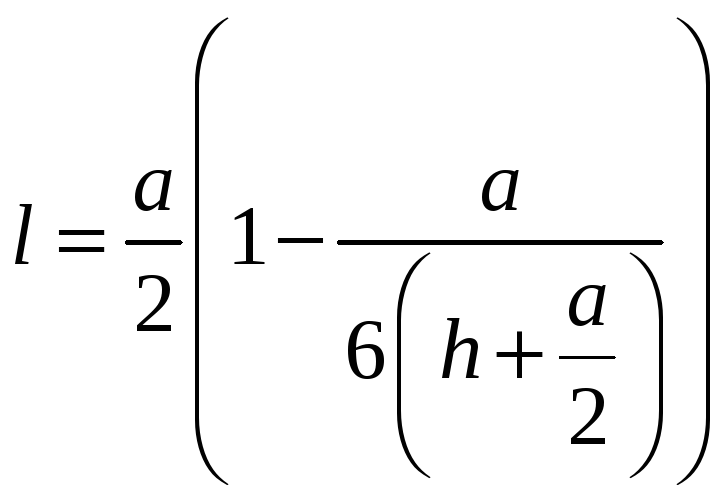 .
.
З
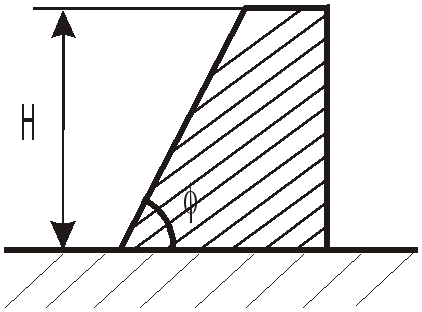
![]() ,
угол наклона грани плотины
,
угол наклона грани плотины![]() .
Расчет вести на 1 погонный метр длины.
Как зависит искомая сила от угла
.
Расчет вести на 1 погонный метр длины.
Как зависит искомая сила от угла
![]() .
.
Ответ:![]() ;
;![]() не зависит от
не зависит от
![]() .
.
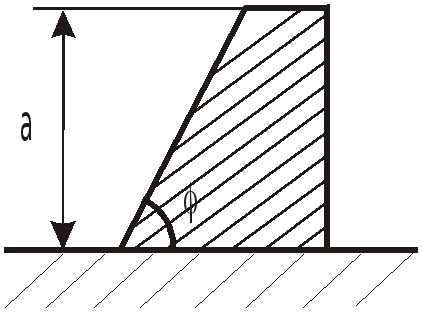
Задача 3.6 Каково должно быть
соотношение между высотой
![]() и шириной
и шириной
![]() ,
чтобы опрокидывающий плотину момент
относительно точки
,
чтобы опрокидывающий плотину момент
относительно точки
![]() составлял бы половину удерживающего
момента? Плотность материала плотины
составлял бы половину удерживающего
момента? Плотность материала плотины
![]() .
.
Ответ:![]() .
.


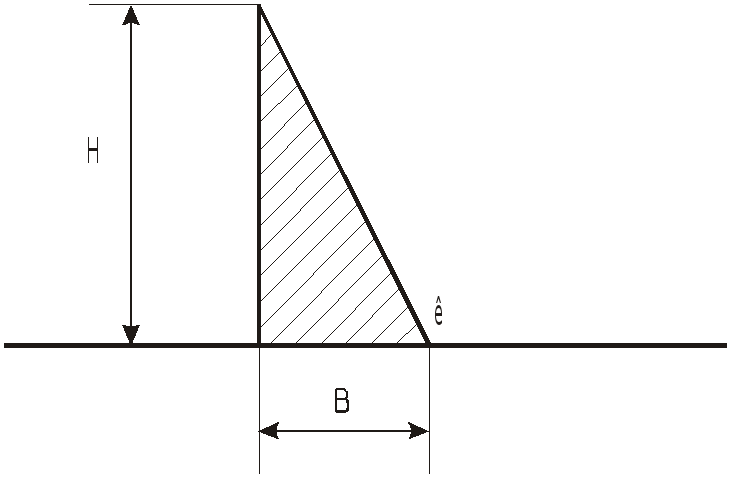
Задача 3.7 Для выпуска нефти из
нефтехранилища устроено квадратное
отверстие размером
![]() и откидной клапан под углом
и откидной клапан под углом
![]() .
Определить усилие
.
Определить усилие
![]() ,
которое нужно приложить к цепи для
открытия клапана, если глубина его
расположения
,
которое нужно приложить к цепи для
открытия клапана, если глубина его
расположения
![]() .
Плотность нефти
.
Плотность нефти
![]() .
.
Ответ:
![]() .
.
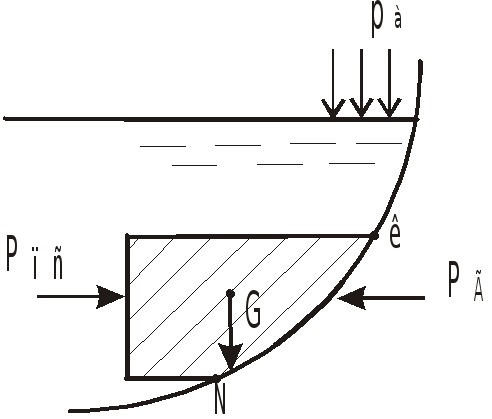
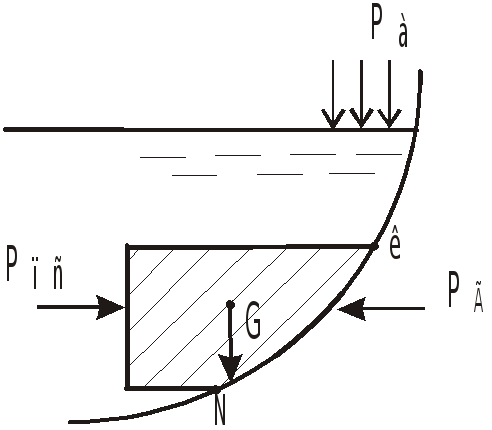
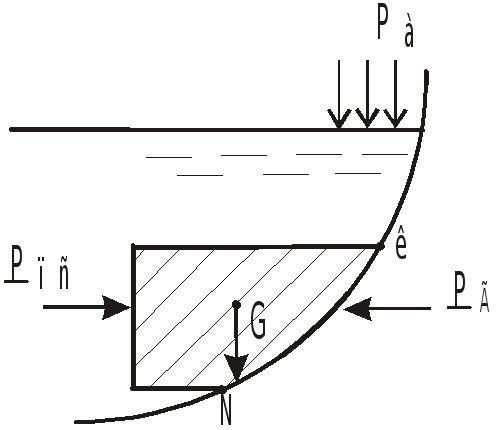
Раздел 4. Сила давления на криволинейную стенку
Сила давления жидкости на криволинейную
стенку
![]() может быть определена через ее проекции
на ортогональные направления:
может быть определена через ее проекции
на ортогональные направления:
![]() .
.
Для криволинейных стенок, имеющих ось или центр симметрии (большинство практических задач), сумма элементарных сил приводится к одной равнодействующей, лежащей в плоскости симметрии или проходящей через центр.
Проекция силы, действующей на криволинейную
стенку, на произвольное направление
![]() ,
равна проекции веса тела давления
,
равна проекции веса тела давления
![]() на это направление:
на это направление:
![]()
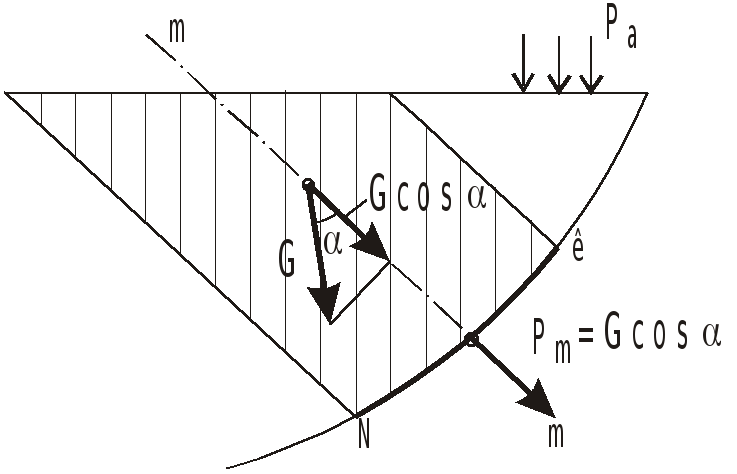
![]() - объем тела давления,
- объем тела давления,
![]() - угол между направлением m-m
и вертикалью.
- угол между направлением m-m
и вертикалью.
Телом давления называется тело, ограниченное стенкой, образующими, проходящими через границы стенки параллельно выбранному направлению, и поверхностью уровня с атмосферным давлением.
Объем тела давления может быть заполнен жидкостью целиком (верхний рисунок) или частично (нижний рисунок, поз.1,2), в ряде случаев может не содержать жидкости вовсе (поз.3).
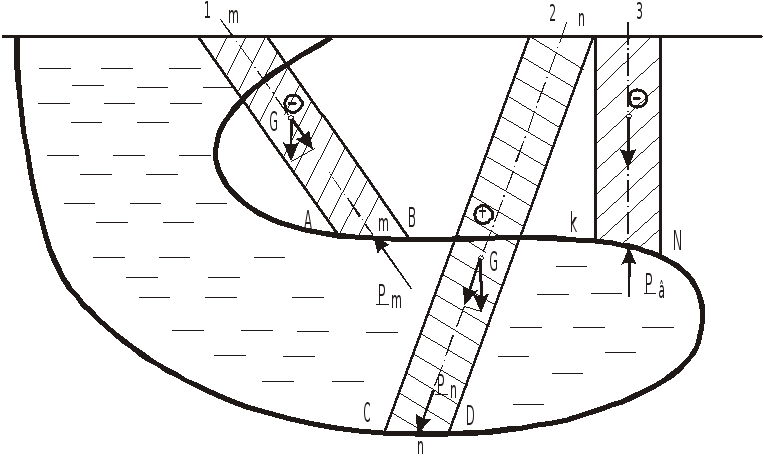

Тело давления, смачивающее стенку,
называется действительным или
положительным, несмачивающее - фиктивным
или отрицательным и обозначается
соответственно
![]() или Ө.
или Ө.
Проекция веса положительного тела давления направлена в ту же сторону, что и соответственная составляющая силы давления (поз.2). Отрицательный знак означает, что эти проекции имеют противоположное направление (поз.1 и 3).
Д

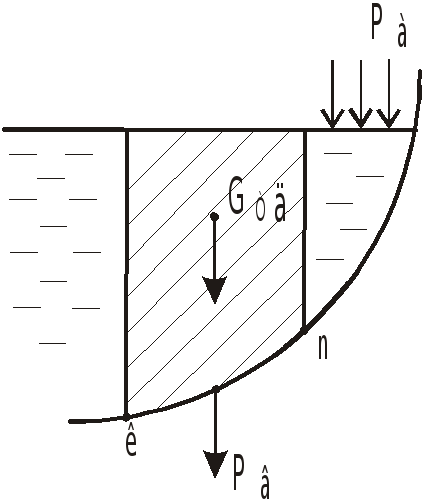
![]() .
.
Вертикальная составляющая
![]() равна весу тела давления.
равна весу тела давления.
Горизонтальная составляющая не может быть определена методом тела давления, так как проекция веса тела давления на горизонтальное направление рана нулю.
И

![]() ,
где
,
где
![]() - сила давления жидкости на плоскую
стенку.
- сила давления жидкости на плоскую
стенку.
Для тел, погруженных в жидкость справедлив закон Архимеда:
На погруженное в жидкость тело действует выталкивающая сила, равная весу жидкости в объеме погруженной части тела.
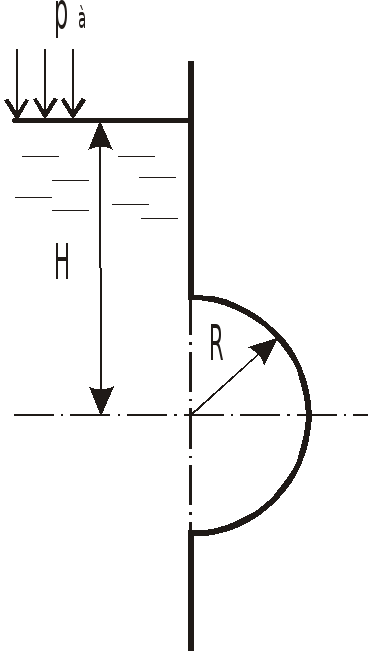
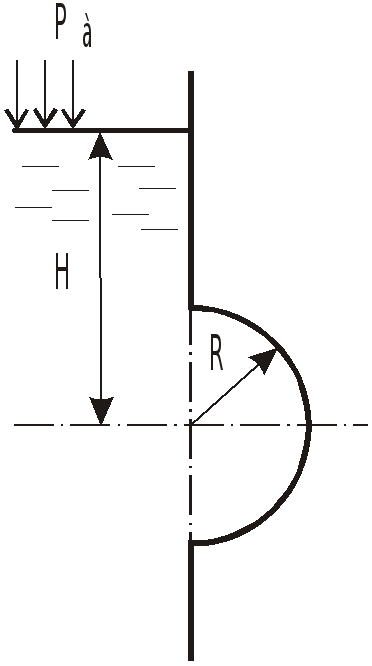
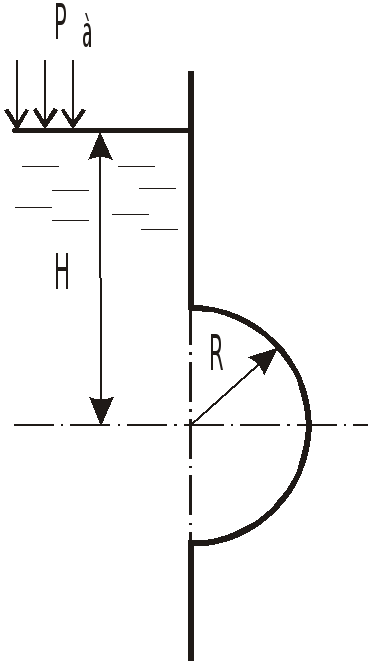
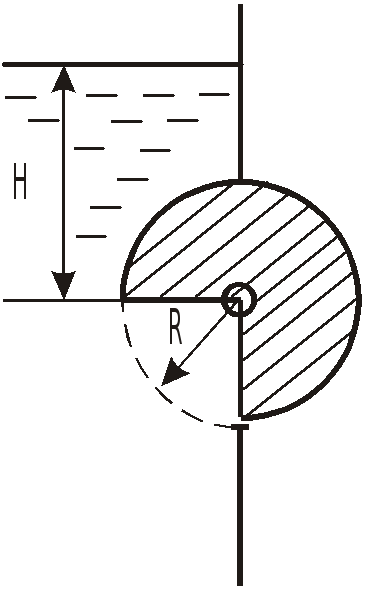
Задача 4.1 Определить полную силу
давления жидкости на полусферическую
крышку, закрывающее круглое отверстие
радиуса
![]() в вертикальной стенке. Напор жидкости
над центром отверстия
в вертикальной стенке. Напор жидкости
над центром отверстия
![]() .
Найти точку приложения этой силы.
.
Найти точку приложения этой силы.
Решение:
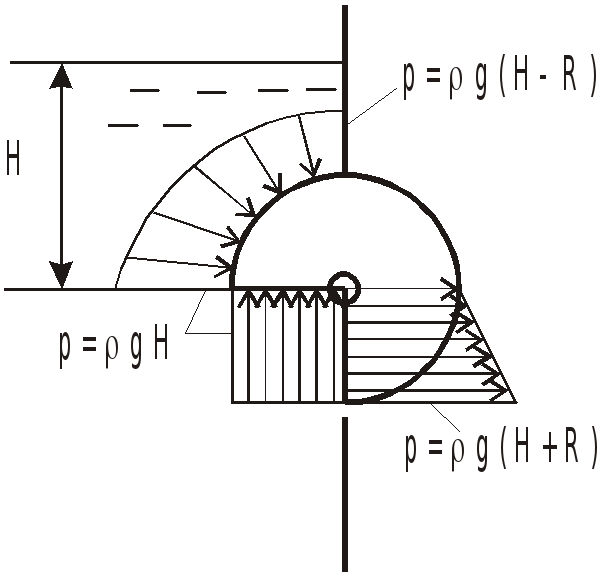
Э


![]() .
Так как каждая элементарная сила проходит
через центр, то и результирующая сила
пройдет через центр. Горизонтальная
составляющая направлена со стороны
жидкости на стенку, вертикальная
составляющая - вниз.
.
Так как каждая элементарная сила проходит
через центр, то и результирующая сила
пройдет через центр. Горизонтальная
составляющая направлена со стороны
жидкости на стенку, вертикальная
составляющая - вниз.
Результирующая сила проходит через
центр под углом
![]() к горизонтали и приложена к стенке:
к горизонтали и приложена к стенке:
![]() .
.
Горизонтальная составляющая
![]() ,
,
где
![]() - давление в центре вертикальной проекции
площадью
- давление в центре вертикальной проекции
площадью
![]() .
.
![]()
По условию задачи
![]() ,
а вертикальная проекция полусферы -
круг с площадью
,
а вертикальная проекция полусферы -
круг с площадью
![]() .
.
![]() .
.
Вертикальная составляющая силы
![]() определяется методом тела давления:
определяется методом тела давления:
![]() .
.
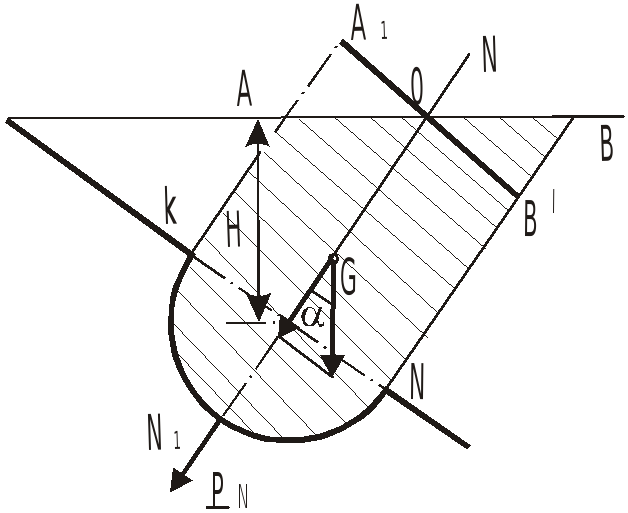
Определим форму тела давления, заключенного между стенкой, свободной поверхностью и вертикальными образующими.
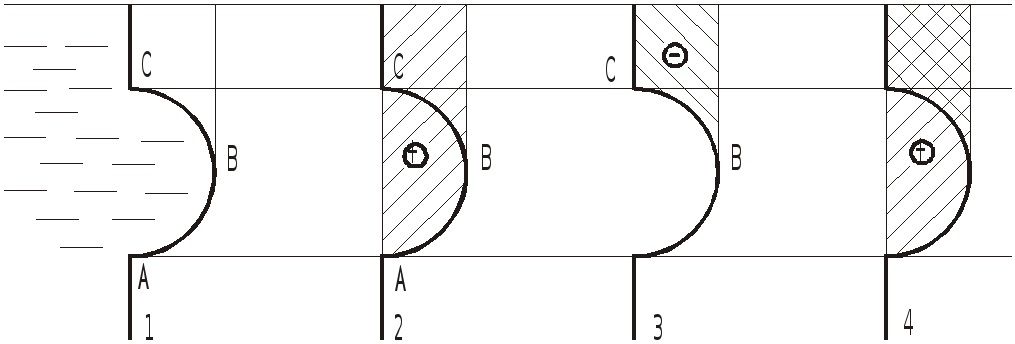
Вертикальные образующие дважды пересекают границу стенки, поэтому разобьем криволинейную стенку на два участка и найдем форму тела давления для каждого из них.
Для участка AB тело давления занимает
объем, заштрихованный на рис. поз. 2.
Направление вертикальной составляющей
![]() совпадает с направлением веса (стенка
смочена) - тело давления положительно.
Для участка BC - тело давления имеет
форму (поз. 3). Тело давления отрицательно
- направление вертикальной составляющей
силы давления
совпадает с направлением веса (стенка
смочена) - тело давления положительно.
Для участка BC - тело давления имеет
форму (поз. 3). Тело давления отрицательно
- направление вертикальной составляющей
силы давления
![]() противоположно направлению веса (см.
эпюру давления).
противоположно направлению веса (см.
эпюру давления).
На всю крышку действует разность сил
![]() ,
равная весу жидкости, заключенной в
полусфере, направленная вниз и равная:
,
равная весу жидкости, заключенной в
полусфере, направленная вниз и равная:
![]() .
.
Полная сила
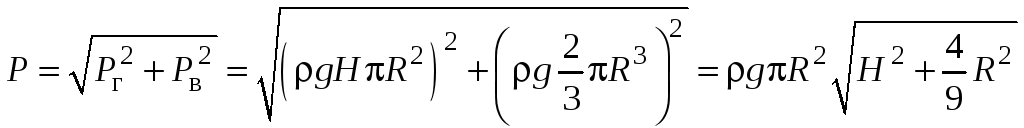 .
.
Угол наклона определяется через
![]() :
:
![]() .
.
З
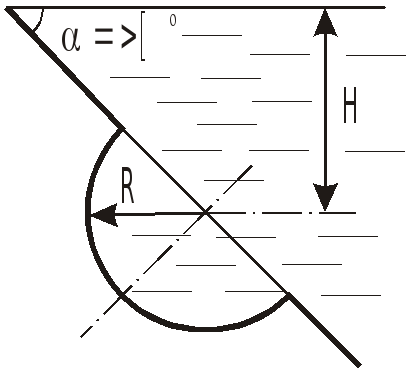
![]() к горизонту, если глубина погружения
центра крышки равна
к горизонту, если глубина погружения
центра крышки равна![]() .
.
Решение:
Э
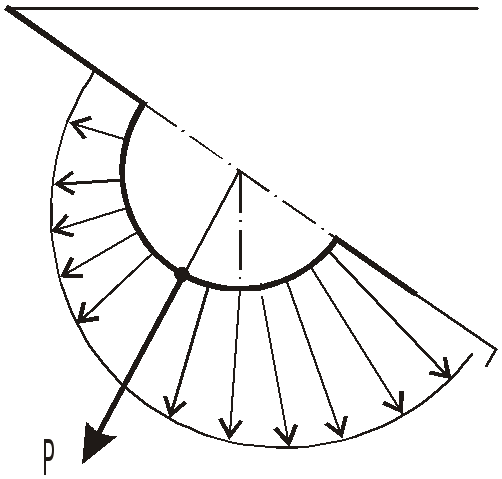
Результирующая сила, очевидно, направлена вниз и влево, проходит через центр и приложена к стенке.
За ортогональные направления для
определения полной силы в данном случае
удобней принять направление вдоль
стенки
![]() и нормально к ней
и нормально к ней
![]() ,
тогда
,
тогда
![]() .
.
Определим методом тела давления эти составляющие:
О
Тело давления
![]() имеет вид, показанный на рис.
имеет вид, показанный на рис.
(образовано стенкой, свободной поверхностью и образующими нормальными к поверхности стенки).
Объем этого тела можно определить как сумму объема полусферы и кругового цилиндра KNAB.
Т.к. объем
![]() ;
;
![]() .
.
Нормальная составляющая силы давления
![]() получим из выражения:
получим из выражения:
![]() .
.
Определение тангенциальной составляющей.
Т
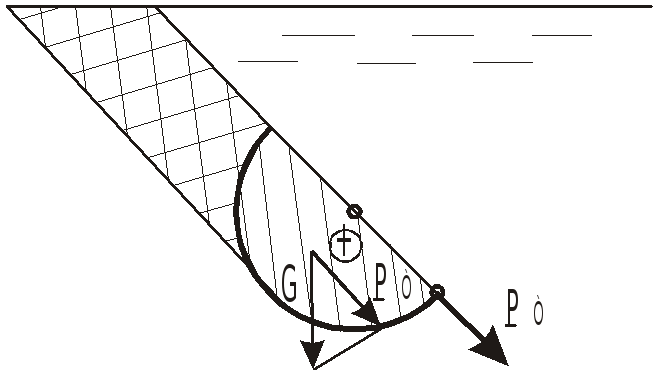
![]() .
.
Полная сила P равна:
 .
.
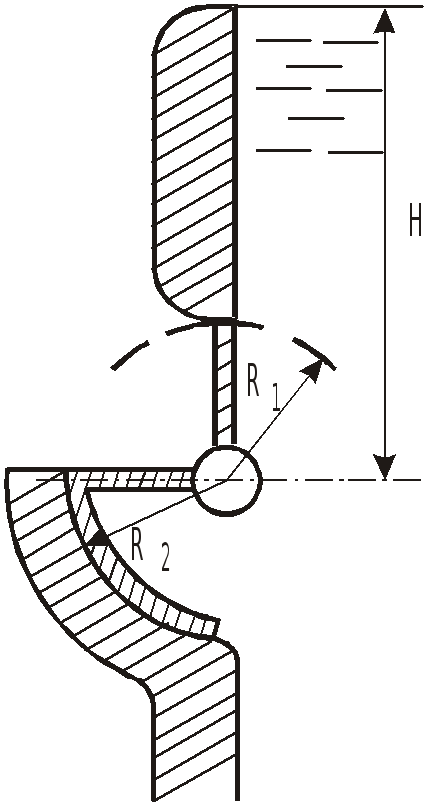
З
![]() и длиной
и длиной![]() .
.
1. Определить усилие на цапфы и момент
от действия воды на затвор в изображенном
на эскизе положении при напоре
![]() .
.
2. Какими будут усилия на цапфы и момент,
если повернуть затвор на
![]() .
.
Р
Определение полной силы.
![]() .
.
Определение горизонтальной составляющей.
Стенка, на которую действует жидкость, состоит из 3-х участков - криволинейной, горизонтальной и вертикальной стенок.
Можно определять силы, действующие на
каждый из участков стенки, а затем их
суммировать. Более простой путь
определения полной силы – выражение
ее через вертикальную и горизонтальную
составляющие.
![]() .
.
На вертикальную проекцию этих участков,
представляющую прямоугольник высотой
![]() и шириной
и шириной
![]() ,
действует сила
,
действует сила
![]() .
.
![]() .
.
Давление в центре масс вертикальной
проекции
![]() ,
следовательно:
,
следовательно:
![]() .
.
Вертикальную составляющую
![]() определим методом тела давления.
определим методом тела давления.
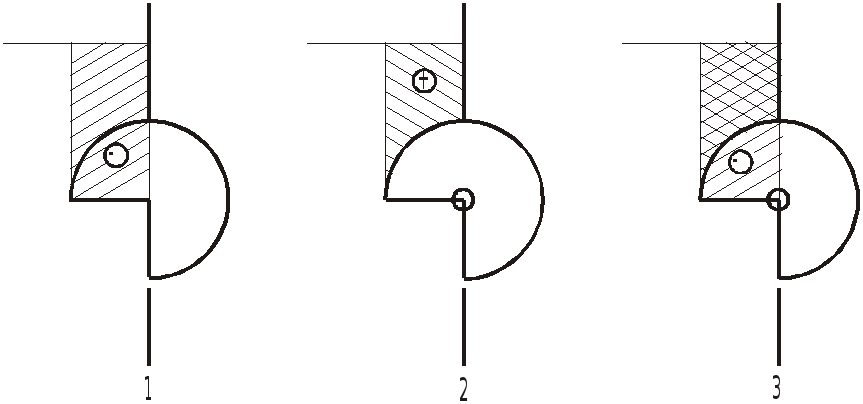
На рис. позиция 1 - тело давления на
горизонтальную плоскую стенку; позиция
2 - на криволинейную стенку; позиция 3 -
тело давления на всю смоченную поверхность
представляет
![]() часть цилиндра.
часть цилиндра.
![]() .
.
Полная сила
![]() .
.
2. Момент силы складывается из моментов от действия силы давления на вертикальный и горизонтальный участки затвора. Сила, действующая на криволинейную стенку, момента не создает, так как проходит через центр вращения.
![]() ;
;
![]() ;
;
![]() .
.
![]()

![]() ;
;
![]() ;
;
![]() -
сила, действующая на вертикальную
стенку:
-
сила, действующая на вертикальную
стенку:
![]() ;
;
![]() ,
где
,
где
![]() - смещение центра давления относительно
центра тяжести.
- смещение центра давления относительно
центра тяжести.
![]() ,
где
,
где
![]() - момент инерции площадки относительно
центральной оси;
- момент инерции площадки относительно
центральной оси;
![]() - расстояние, отсчитанное в плоскости
площадки от центра масс до поверхности
атмосферного давления.
- расстояние, отсчитанное в плоскости
площадки от центра масс до поверхности
атмосферного давления.
Для прямоугольника
![]() ,
где
,
где
![]() - ширина,
- ширина,
![]() - высота.
- высота.
Для вертикального участка затвора
![]() ;
;
![]() ;
;
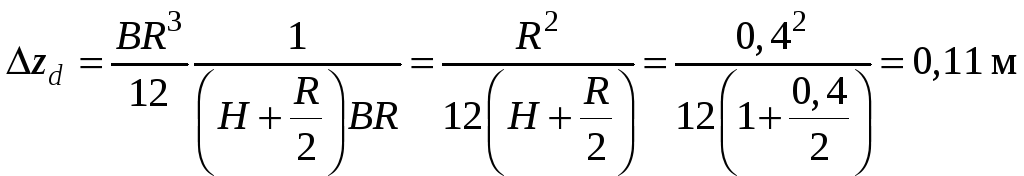 .
.
![]() ;
;
![]() ;
;
![]() .
.
I. При повороте затвора на
![]() он
займет положение, показанное на рис.
он
займет положение, показанное на рис.
Полная сила
![]() .
.
П
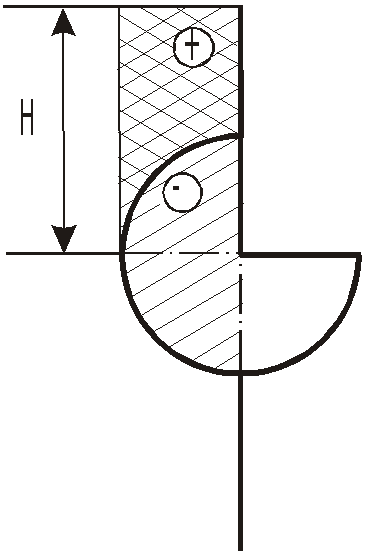
![]() .
.
![]() .
.
Тело давления представляет собой половинку цилиндра:
![]() .
.
Полная сила
![]() .
.
Момент этой силы относительно центра
вращения
![]() ,
т.к. сила проходит через центр.
,
т.к. сила проходит через центр.
Ответ: 1.
![]() ;
;
![]() ;
;
2.
![]() .
.