Раздел 3. Сила давления жидкости на плоскую стенку

Сила , действующая со стороны жидкости на плоскую стенку, направлена по нормали к стенке, является равнодействующей элементарных сил давления и равна:

,

где - давление в центре масс стенки - точке C.

,

где - глубина погружения точки C относительно поверхности с давлением ,

- давление на свободной поверхности или любой другой поверхности уровня.

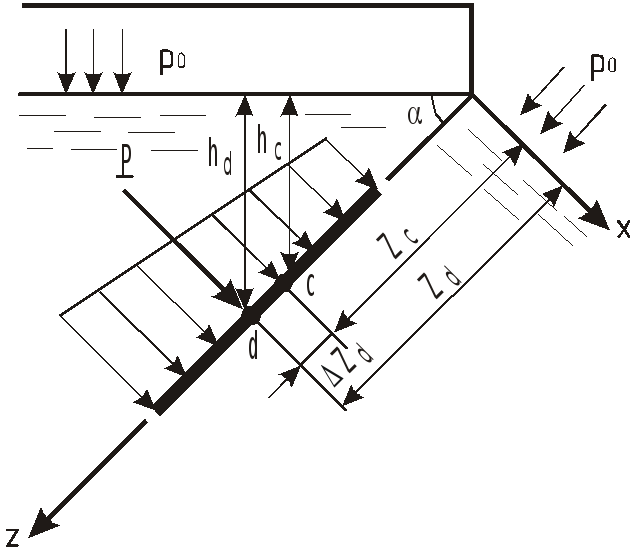
Оси координат свяжем со стенкой и проведем их следующим образом: ось x – совместим с линией пересечения свободной поверхности жидкости и стенки, ось z – в плоскости стенки, ось y – перпендикулярно плоскости x0z.

Сила приложена в точке - центре давления, который смещен на относительно точки C и проходит через центр масс эпюры давления.

,

где - момент инерции стенки относительно центральной оси, - площадь стенки, отсчитывается в плоскости стенки от свободной поверхности с давлением, равным атмосферному.

.

Если давление на свободной поверхности отличается от атмосферного, то необходимо найти фиктивное положение поверхности уровня с давлением, равным атмосферному, и координату отсчитывать от этой поверхности.

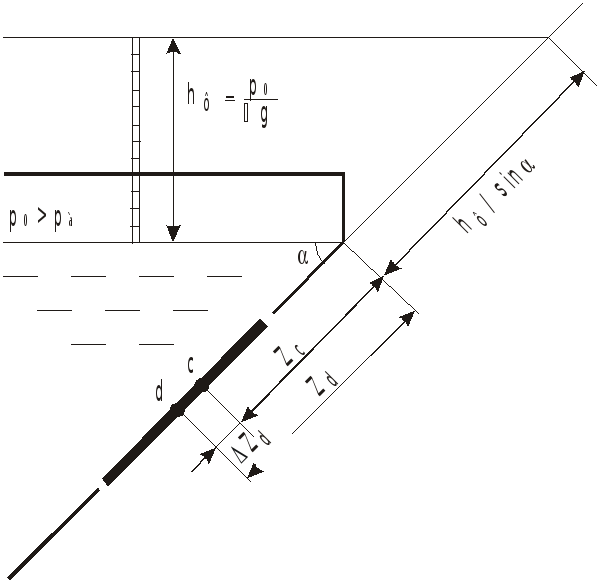
При поверхность уровня с атмосферным давлением расположится выше свободной поверхности на , в этом случае координата . При поверхность уровня с расположится ниже свободной поверхности на , где - вакуумное давление.

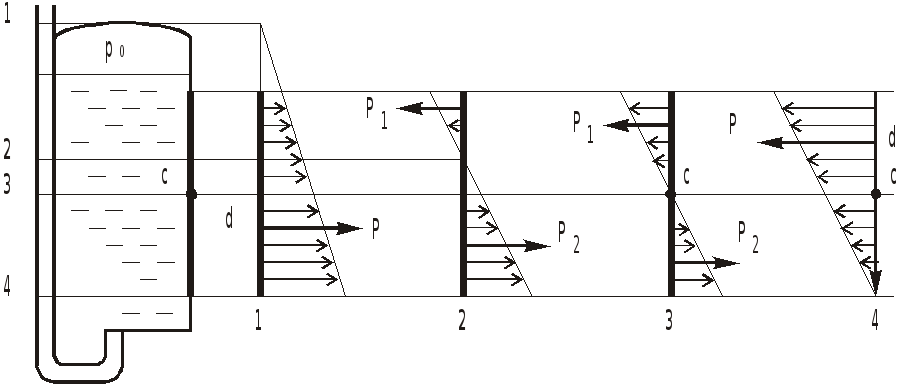
Если поверхность атмосферного давления пересекает стенку, направление сил давления изменяется.

На рис. показаны эпюры, данные для нескольких характерных положений поверхности с атмосферным давлением.

Цифрами 1...4 обозначены уровни жидкости в пьезометре.

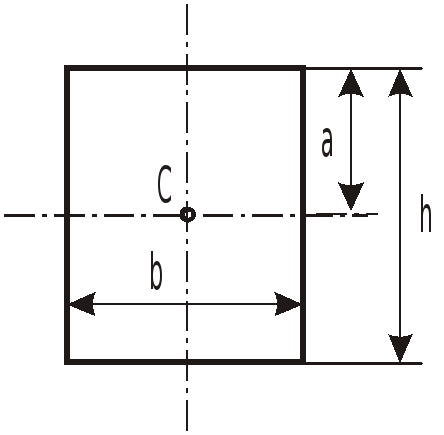
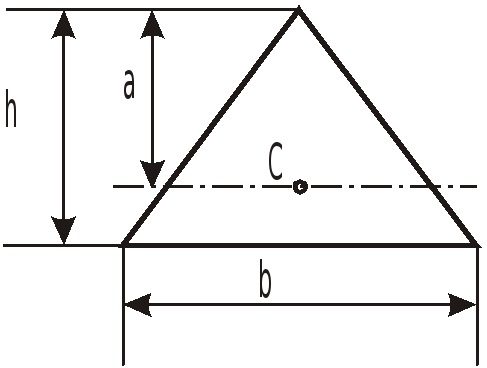
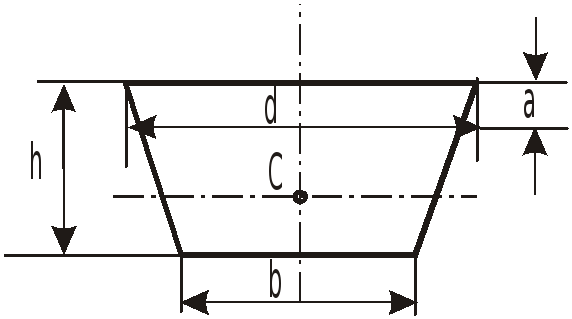
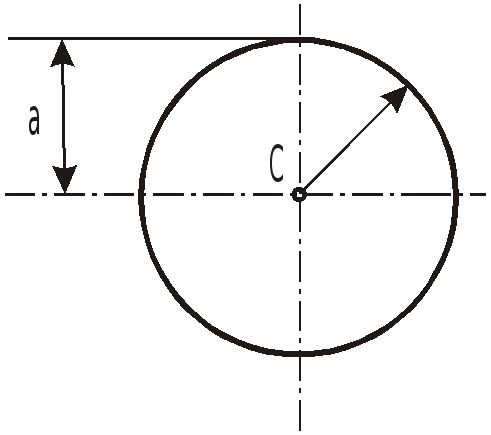
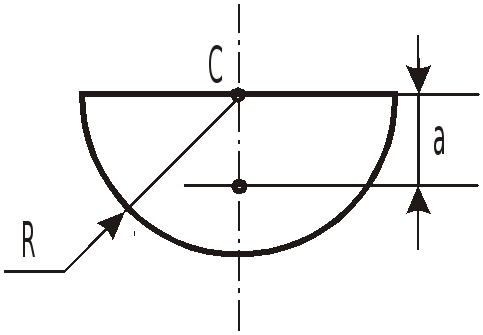
Необходимые при решении задач зависимости для определения площади, момента инерции и координаты центра тяжести различных по форме площадок приведены в таблице.

Таблица.

Фигура	Момент инерции отн. оси, прох. через C “Jcx”	Координата центра тяжести C “a"	Площадь S

Задача 3.1 Найти положение оси шарнира , при котором подъем верхнего уровня воды выше вызвал бы автоматическое опрокидывание щита, если ,.

Дано:

; ; .

Найти:

Решение:

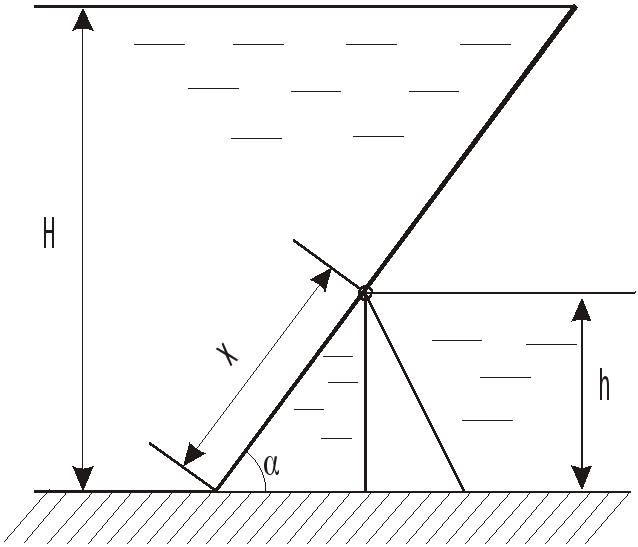
Эпюры сил давления имеют вид, представленный на рисунке.

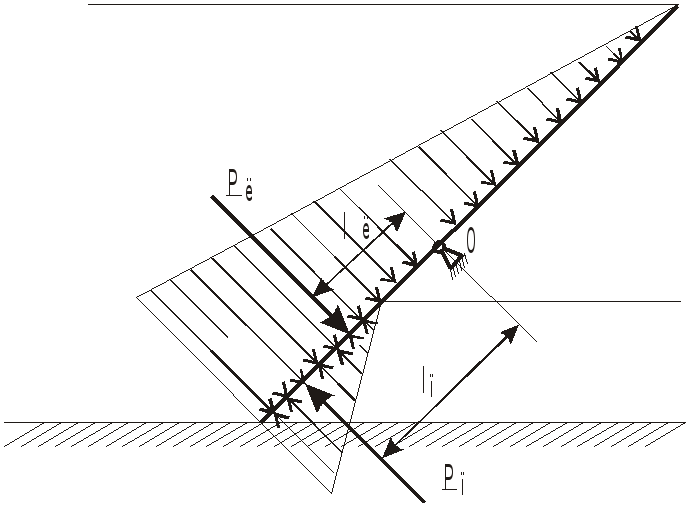
Условие равновесия щита - сумма моментов сил равна нулю.

; , где

- силы давления воды, действующие слева и справа,

- плечи этих сил.

Площадки, на которые действуют силы представляют плоские стенки.

Сила , действующая на плоскую стенку со стороны жидкости, определяется как

, а - давление в точке С - центре масс площадки, где

, - глубина погружения точки C относительно свободной поверхности, - площадь.

Сила приложена в точке - центре давления, который смещен относительно центра масс и расстояние в плоскости площадки от до свободной поверхности , где - момент инерции площадки относительно центральной оси.

Для прямоугольника высотой и шириной - .

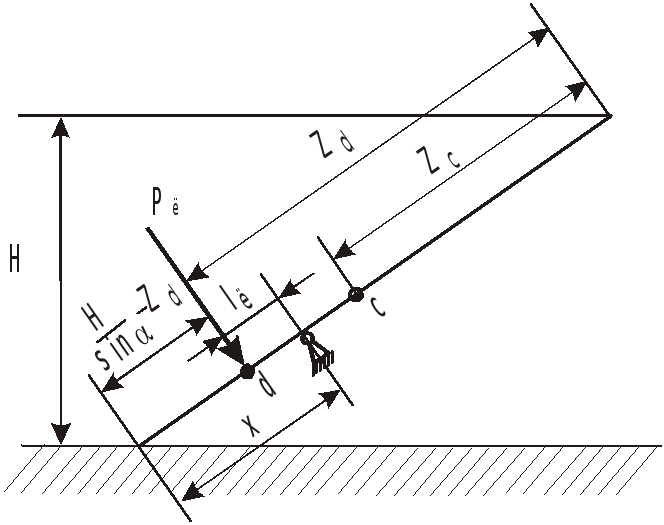
Определим момент силы , действующей слева:

.

;

учитывая, что и ,

где - ширина плотины, находим:

.

Плечо силы ;

; ; ;

;

.

Для плоской площадки, эпюра давлений которой представляет треугольник, можно было сразу определить положения центра масс эпюры - на 1/3 от основания.

О

пределение момента силы, действующей справа:

;

;

.

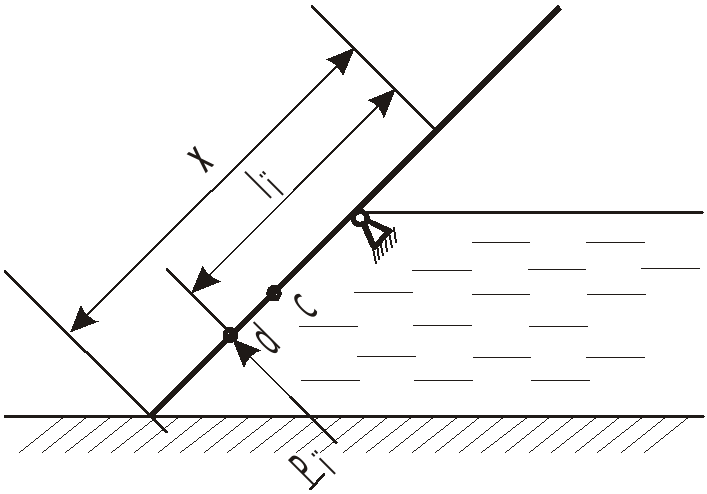
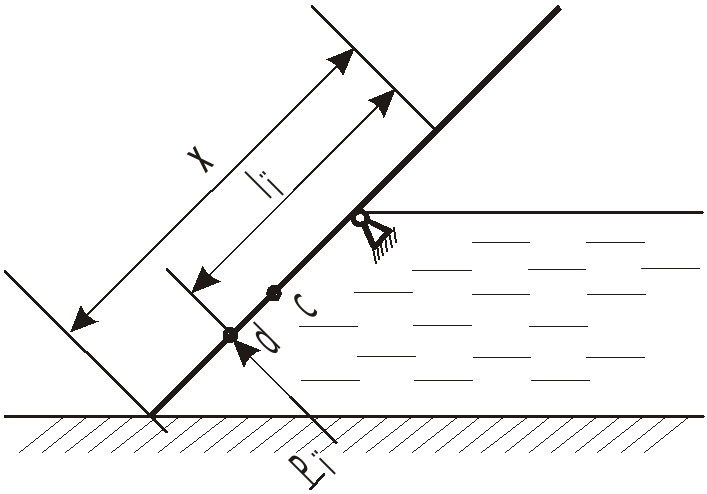
Так как , ,

, откуда:

.

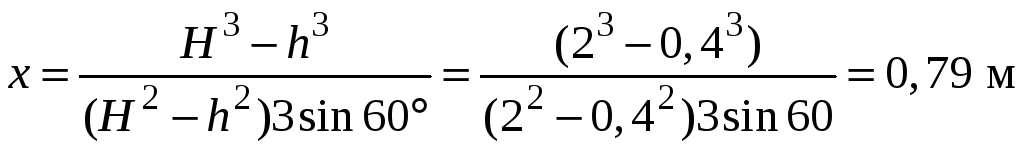Ответ:.