
- •Раздел 1. Свойства жидкости
- •Свойства давления.
- •Раздел 2. Закон распределения давления в жидкости
- •Раздел 3. Сила давления жидкости на плоскую стенку
- •З адача 3.2
- •Раздел 4. Сила давления на криволинейную стенку
- •Задача 4.4
- •Раздел 5. Относительное равновесие жидкости в сосудах, движущихся прямолинейно с постоянным ускорением
- •Определение сил, действующих на заднюю и переднюю стенки методом “тела давления”
- •Раздел 6. Относительное равновесие жидкости во вращающихся сосудах Равномерное вращение цилиндрического сосуда вокруг вертикальной оси.
- •Равномерное вращение цилиндрического сосуда вокруг оси, не совпадающей с вертикалью.
- •Раздел 7. Уравнение бернулли для потока идеальной жидкости
- •Раздел 8. Уравнение бернулли для потока реальной жидкости.
- •Раздел 9. Течение жидкости в каналах некруглого поперечного сечения.
- •Раздел 10. Истечение жидкости через отверстия и насадки
- •Истечение через отверстия
- •И стечение через насадки
- •Определение коэффициентов истечения опытным путем.
- •Раздел 11. Гидравлический расчет трубопроводов Простой трубопровод.
- •Последовательное соединение трубопроводов.
- •Параллельное соединение трубопроводов.
- •Расчет сложного трубопровода.
- •1 Приближение
- •2 Приближение
1 Приближение
![]() ;
;
![]() .
.
2 Приближение
![]() ;
;
![]() .
.
После 2 приближения
![]() .
.
Необходимо 3 приближение.
![]() .
.
![]() .
.
Разница между значениями скорости
![]() и
и
![]() мала, и относительная погрешность после
3 приближения
мала, и относительная погрешность после
3 приближения
![]() намного меньше заданных 5%.
намного меньше заданных 5%.
Расход воды:
![]() .
.
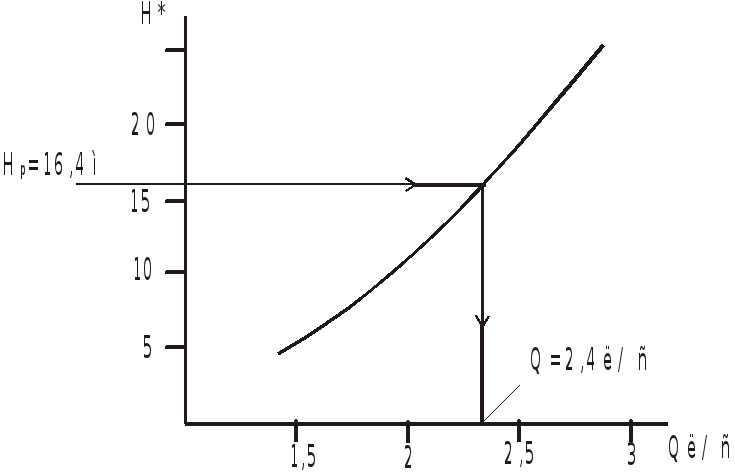
Задачу можно решить и графическим методом.
Построим характеристику трубопровода
![]() или
или
![]() .
.
Зададимся несколькими значениями расхода и определим потери напора при выбранных значениях:
![]()
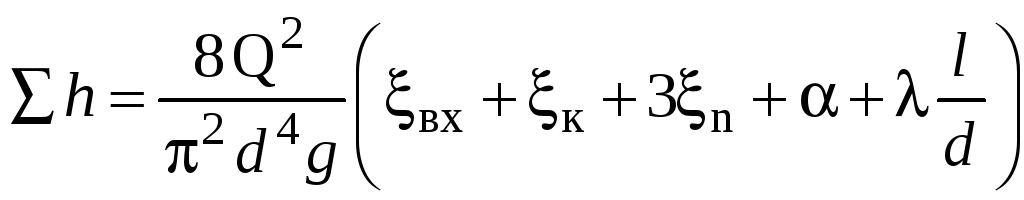 ;
;
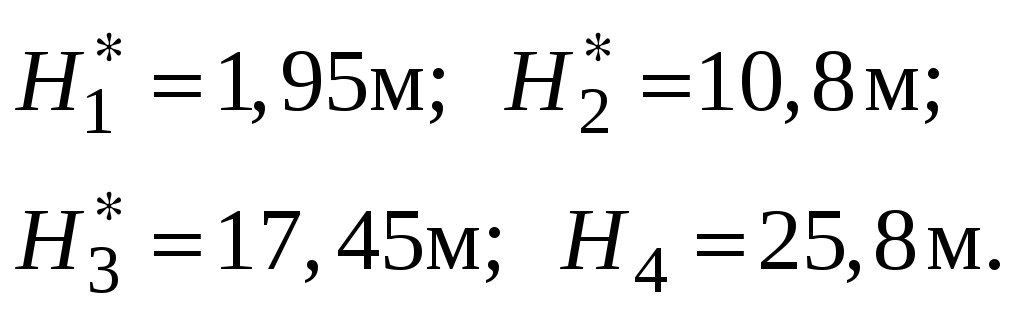
Построим график
![]() .
.
Найдем располагаемый напор:
![]() .
.
Этому напору соответствует расход
![]() .
.
З
Определить расход воды через сифонный
трубопровод, изображенный на рисунке,
если высота
![]() .
Общая длина трубы
.
Общая длина трубы
![]() ,
диаметр
,
диаметр
![]() .
.
Учесть потери при входе
![]() ,
в коленах
,
в коленах
![]() ,
в вентиле
,
в вентиле
![]() .
.
Подсчитать вакуум в верхнем сечении
трубы
![]() ,
если длина участка от входа в трубу до
этого сечения
,
если длина участка от входа в трубу до
этого сечения
![]() .
Коэффициент вязкости воды
.
Коэффициент вязкости воды
![]() .
.
Дано:
![]() ;
;
![]() ;
;
![]() .
.
Найти:
![]() .
.
Решение:
-
Определение расхода
 .
.
Запишем уравнение Бернулли для сечений 0-0—1-1:
![]() ;
;
![]() ;
;
откуда определим действительную скорость
![]() :
:
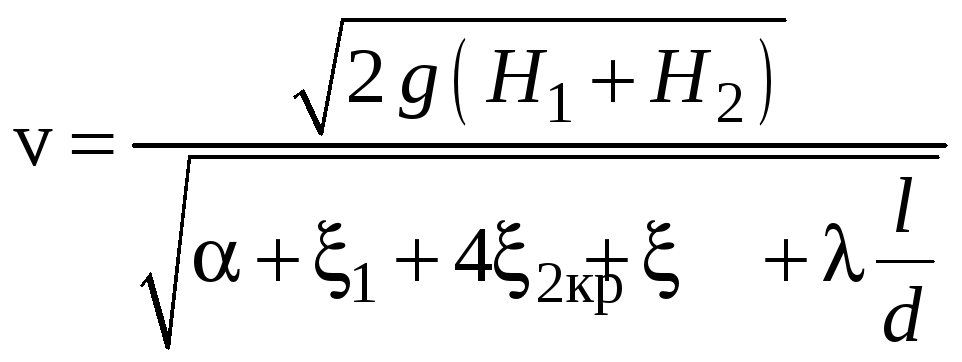 .
.
Предположим, что режим течения турбулентный
и коэффициент трения в первом приближении
![]() ,
тогда:
,
тогда:
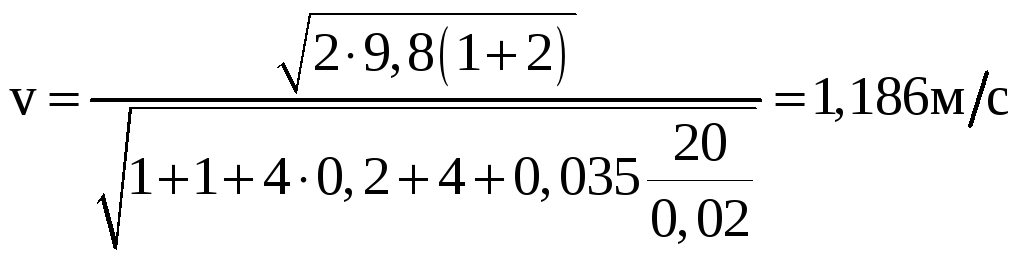 .
.
Уточняем значение
![]() :
:
![]() .
.
Режим турбулентный.
![]() .
.
Скорость 2 приближения:
![]() .
.
Погрешность вычисления
![]() .
.
Необходимо 3 приближение
![]() ;
;
![]() .
.
Расход
![]() .
.
-
Определение давления в верхнем сечении:
![]()
![]() ;
;
![]() ;
;
![]() ;
;
абсолютное давление
![]() ;
;
вакуум
![]() .
.
З

1.Определить коэффициент сопротивления
крана
![]() ,
при котором расход жидкости
,
при котором расход жидкости
![]() в ветвях трубопровода будет одинаковым,
если расход в неразветвленной части
трубопровода
в ветвях трубопровода будет одинаковым,
если расход в неразветвленной части
трубопровода
![]() .
.
Диаметры всех участков трубопровода
одинаковы
![]() ,
длины
,
длины
![]() .
Местными потерями, кроме крана, пренебречь.
.
Местными потерями, кроме крана, пренебречь.
2. Как нужно изменить
![]() при увеличении общего расхода, чтобы
сохранить равенство расходов в ветвях?
при увеличении общего расхода, чтобы
сохранить равенство расходов в ветвях?
Решение.
При параллельном соединении трубопроводов
потери напора в них одинаковы
![]() .
В первом трубопроводе учитываем только
потери по длине, во втором к потерям по
длине добавляются потери в кране.
.
В первом трубопроводе учитываем только
потери по длине, во втором к потерям по
длине добавляются потери в кране.
![]() .
.
Учитывая, что по условию задачи
![]() и
и
![]() ,
следовательно
,
следовательно
![]() ,
,
![]() и
и
![]() ,
получим:
,
получим:
![]() ;
;
откуда:
![]() .
.
Режим течения в ветвях трубопровода
одинаковый. Число Рейнольдса может быть
определено по величине расхода
![]() ;
;
![]() .
.
Режим течения ламинарный, коэффициент
потерь
![]() определяется по формуле:
определяется по формуле:
![]() ;
;
![]() .
.
Ответ: 1.
![]()
2. При увеличении расхода возрастает число Рейнольдса, и, следовательно,
уменьшается коэффициент сопротивления
![]() ;
;
для сохранения равенства расходов в
ветвях
![]() должно уменьшаться.
должно уменьшаться.
З
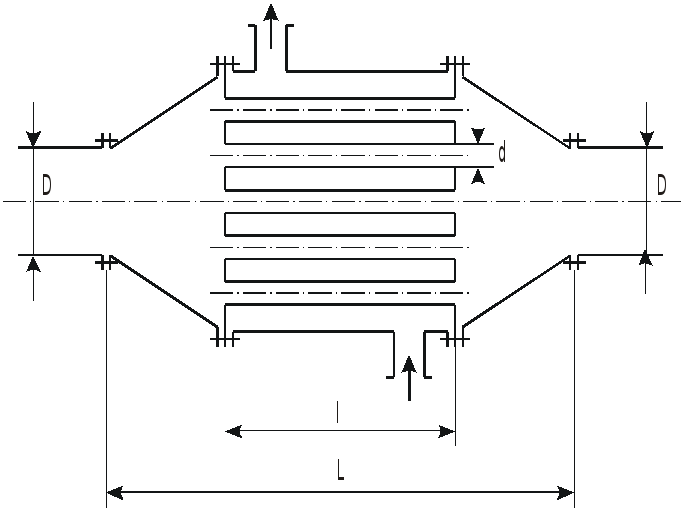
На трубопроводе диаметром
![]() установлен трубчатый подогреватель.
Сумма живых сечений трубок
установлен трубчатый подогреватель.
Сумма живых сечений трубок
![]() равна площади сечения трубопровода;
длина трубок
равна площади сечения трубопровода;
длина трубок
![]() .
.
Пренебрегая сопротивлениями в конусах
и потерями на вход в трубки и на выход
из них, определить, во сколько раз
сопротивление подогревателя больше
сопротивления участка трубопровода
диаметром
![]() и длиной
и длиной
![]() ,
на месте которого установлен подогреватель.
(Использовать формулу Блазиуса).
,
на месте которого установлен подогреватель.
(Использовать формулу Блазиуса).
Решение.
Потери в трубе диаметром
![]() и длиной
и длиной
![]() :
:
![]() .
.
Потери в подогревателе равны потерям
в одной трубке диаметром
![]() и длиной
и длиной
![]() ,
т.к. пучок трубок представляет собой
параллельное соединение труб:
,
т.к. пучок трубок представляет собой
параллельное соединение труб:
![]() .
.
По условию площади живых сечений всех
трубок и площадь трубы равны, следовательно
![]() .
.
Искомое отношение
![]() .
.
По формуле Блазиуса :
![]() ;
;
следовательно
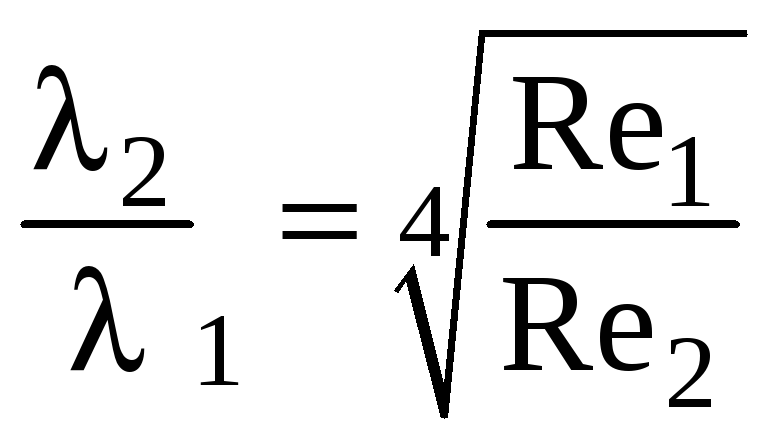 .
.
Критерий Рейнольдса
![]() .
.
Учитывая, что
![]() и
и
![]() в обоих случаях одинаковы, получаем
в обоих случаях одинаковы, получаем
![]() ;
;
![]()
Ответ: сопротивление подогревателя в 16 раз больше сопротивления трубы.
Задача 11.6
Определить, при каком проходном сечении
дросселя расходы в параллельных ветвях
трубопровода будут одинаковыми, если
длины
![]() ,
диаметры труб
,
диаметры труб
![]() .
Коэффициент расхода дросселя
.
Коэффициент расхода дросселя
![]() ;
вязкость жидкости
;
вязкость жидкости
![]() ;
расход жидкости перед разветвлением
;
расход жидкости перед разветвлением
![]() .
Трубопровод считать гидравлически
гладким.
.
Трубопровод считать гидравлически
гладким.
Д
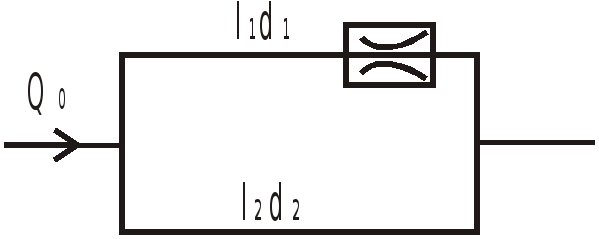
Найти
![]() .
.
Решение.
Так как при параллельном соединении труб потери в ветвях равны, имеем:
![]() или
или
![]() .
.
Т.к.
![]() и
и
![]() по условию задачи,
по условию задачи,
то
![]() и
и
![]() ,
потери в дросселе
,
потери в дросселе
![]() .
.
Критерий Рейнольдса
![]() .
.
Режим течения турбулентный, следовательно:
![]() ;
;
![]() .
.
Через дроссель проходит расход
![]() ,
при этом перепад напора на дросселе
составляет
,
при этом перепад напора на дросселе
составляет
![]() .
.
![]() ,
,
откуда
![]() ;
;
т.к.
![]() ,
,
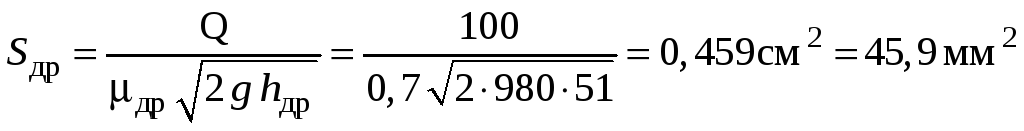 .
.
Ответ:
![]() .
.
З
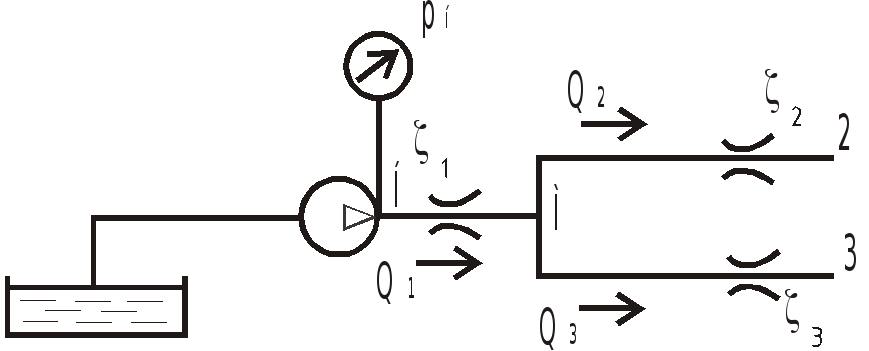
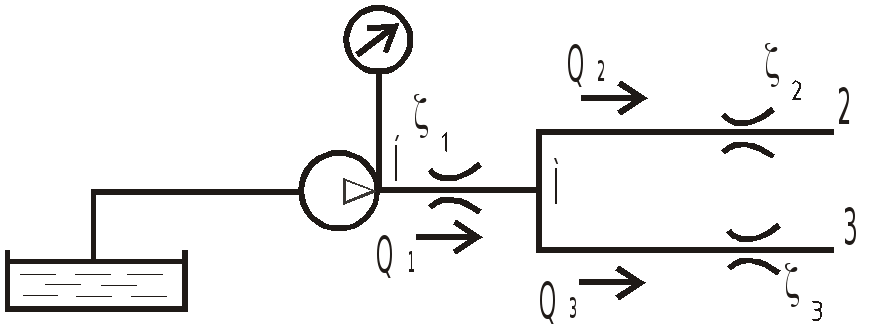
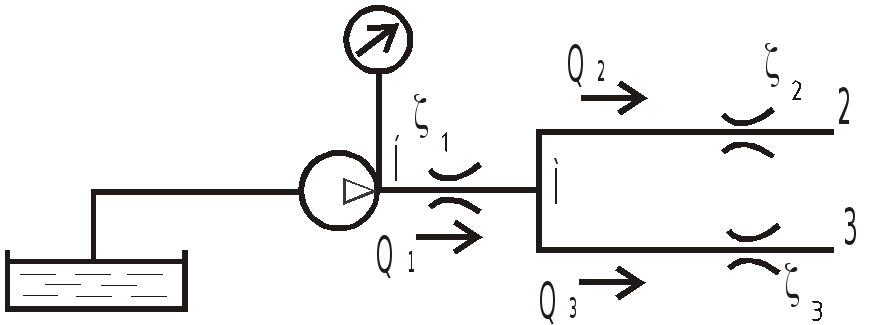
Насос обеспечивает расход воды
![]() по трубопроводу, в котором установлен
дроссель с коэффициентом сопротивления
по трубопроводу, в котором установлен
дроссель с коэффициентом сопротивления
![]() .
В точке М трубопровод разветвляется на
два трубопровода, один из которых
содержит дроссель с коэффициентом
сопротивления
.
В точке М трубопровод разветвляется на
два трубопровода, один из которых
содержит дроссель с коэффициентом
сопротивления
![]() ,
а другой с
,
а другой с
![]() .
Трубопроводы расположены в горизонтальной
плоскости, на выходе давление атмосферное.
.
Трубопроводы расположены в горизонтальной
плоскости, на выходе давление атмосферное.
Пренебрегая потерями на трение по длине,
определить расходы жидкости в ветвях
трубопровода и давление
![]() насоса.
насоса.
Диаметры всех труб одинаковы
![]() .
.
Решение:
Потери напора во второй и третьей ветвях
равны, т.к. в начале каждой из них давление
одинаково и равно
![]() ,
а на выходе давление атмосферное.
,
а на выходе давление атмосферное.
![]()
Т.к. учитываются только потери на
дросселях, то
![]() .
.
Откуда
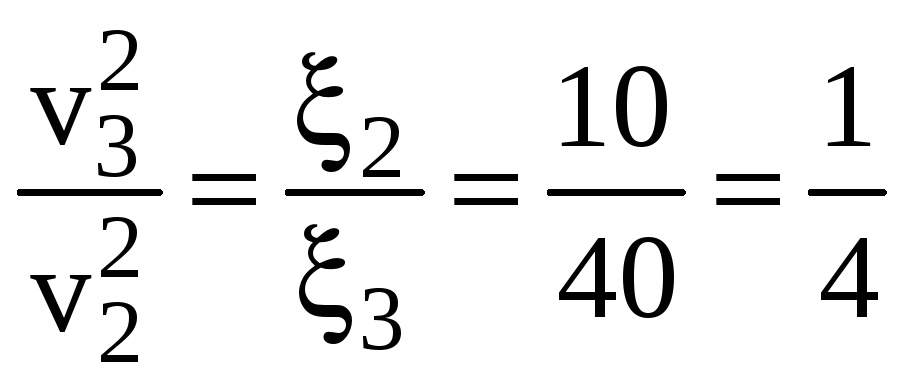 и
и
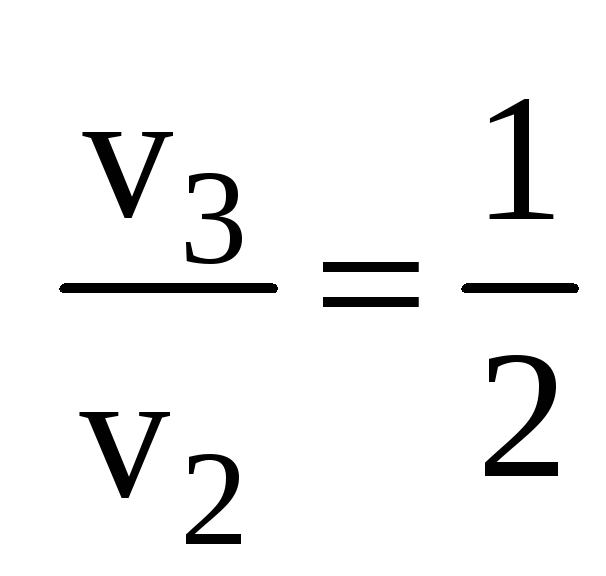 .
.
По условию
![]() ,
следовательно
,
следовательно
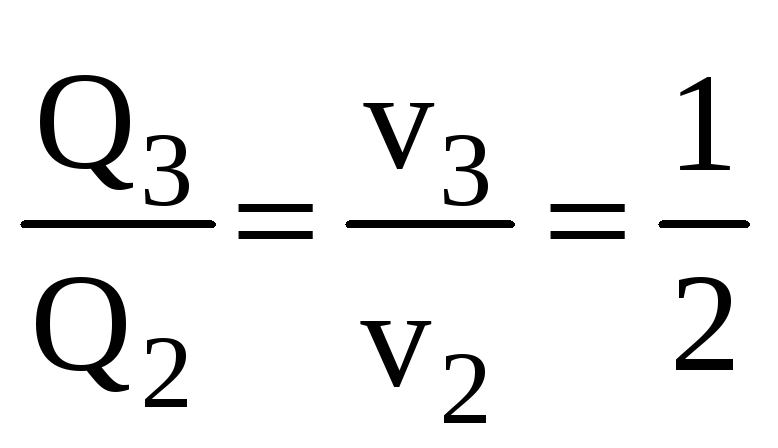 и
и
![]() .
.
В точке М поток разделяется на два
потока, следовательно
![]() ;
;
![]() и
и
![]() .
.
Из уравнения Бернулли для сечений
![]() первого трубопровода имеем:
первого трубопровода имеем:
![]() ;
;
для сечений М-3 третьего трубопровода:
![]() .
.
Исключая из последних уравнений
![]() ,
получаем:
,
получаем:
![]() ;
;
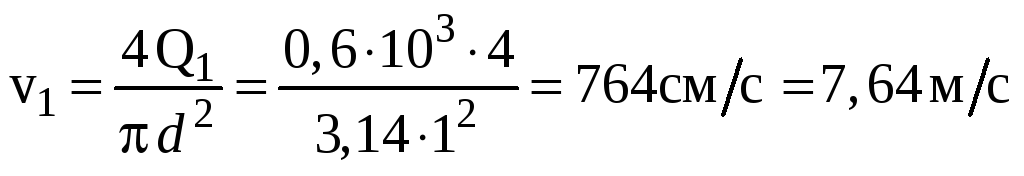 ;
;
![]() ;
;
![]() ;
;
![]() .
.
Ответ:
![]() .
.
З
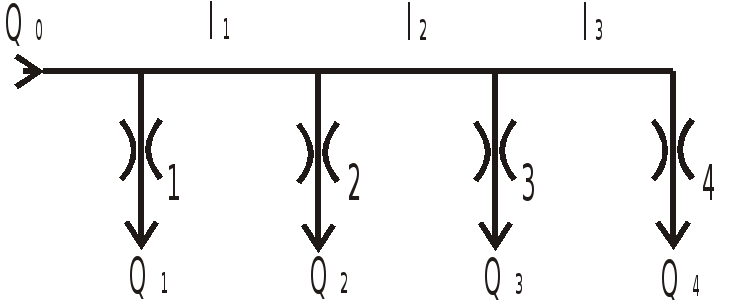
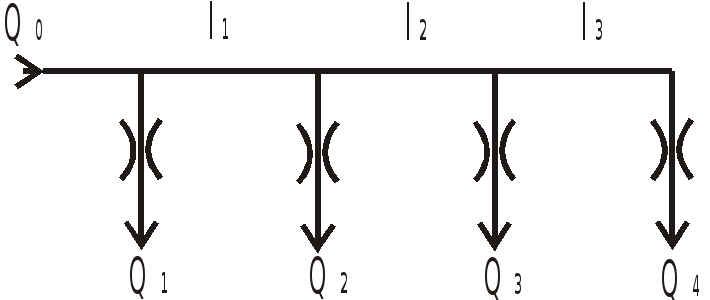
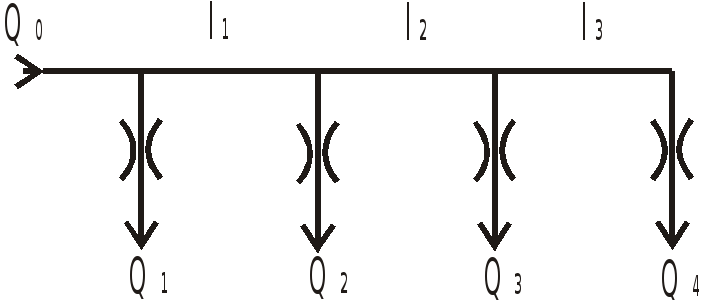
По трубопроводу диаметром
![]() и длиной
и длиной
![]() движется жидкость, истекающая по пути
следования в атмосферу через дроссели
1…4 с одинаковыми коэффициентами
сопротивления
движется жидкость, истекающая по пути
следования в атмосферу через дроссели
1…4 с одинаковыми коэффициентами
сопротивления
![]() .
.
Найти соотношения между длинами участков
трубопровода
![]() ,
если
,
если
![]() .
.
Считать, что движение жидкости происходит в области квадратичного сопротивления.
Решение:
Дано:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Найти
![]() .
.
В
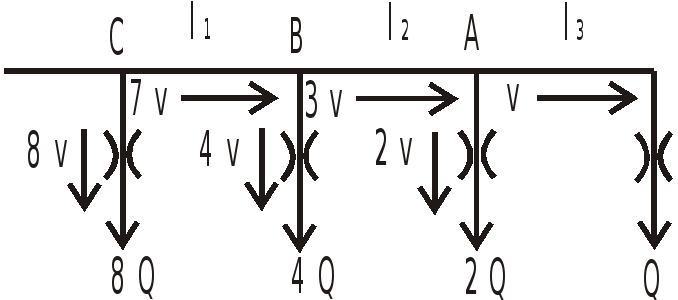
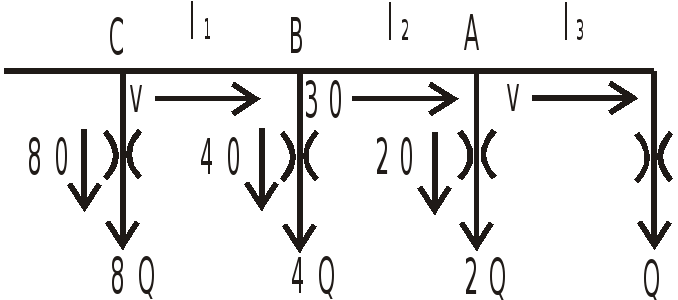
![]() ,
тогда
,
тогда
![]() .
.
Точки разветвления трубы (узлы) обозначим буквами A, B, C.
К узлу A подходит
жидкость с расходом
![]() .
.
К узлу B -
![]() .
.
В трубах постоянного сечения скорости
пропорциональны расходу
![]() ,
следовательно, скорости на различных
участках относятся так же, как расходы
на этих участках.
,
следовательно, скорости на различных
участках относятся так же, как расходы
на этих участках.
Потери на участках A-3 и A-4 одинаковы, так как начинаются оба участка в одной и той же точке A, а на выходе давление также одинаковое, равное атмосферному:
![]() .
.
Аналогично можно записать:
![]() ;
;
![]() ,
,
Выражая потери через скорости, получим:
Узел A.
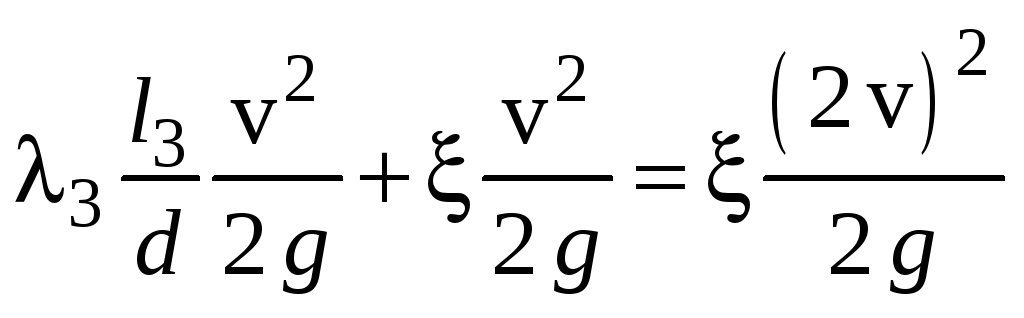 ;
;
Узел B.
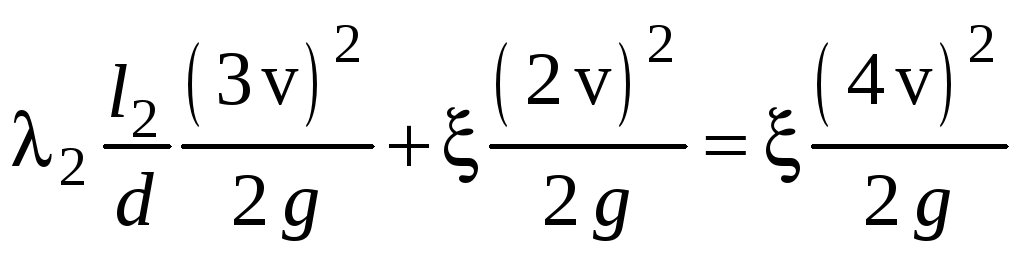 ;
;
Узел С.
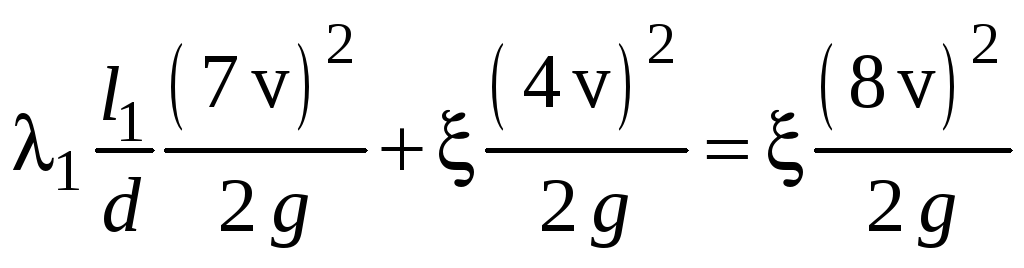 .
.
После преобразований получим:
![]() .
.
Так как по условию
![]() не зависит от числа
не зависит от числа
![]() (IV
зона сопротивления), а зависит только
от качества трубы,
(IV
зона сопротивления), а зависит только
от качества трубы,
![]() ,
и отношение длин участков может быть
выражено как:
,
и отношение длин участков может быть
выражено как:
![]() .
.
З
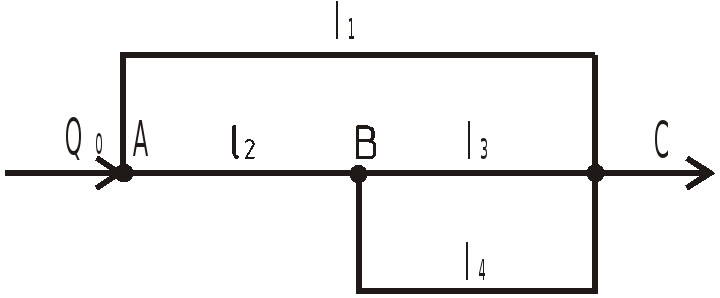
На рисунке показан сложный трубопровод.
Определить расходы в каждом из простых
трубопроводов, если длины равны:
![]() ,
а суммарный расход
,
а суммарный расход
![]() .
.
Считать режим течения в подводящем трубопроводе ламинарным, а диаметры всех трубопроводов одинаковыми.
Решение:
В узле A поток с расходом
![]() разделяется на два потока с расходами
разделяется на два потока с расходами
![]() и
и
![]() :
:
![]() .
.
В узле B поток с расходом
![]() разделяется на два потока с расходами
разделяется на два потока с расходами
![]() и
и
![]() :
:
![]() .
.
Суммарные потери на участке B-C, состоящем из параллельно соединенных 3 и 4 участков, равны потерям на каждом из них:
![]() .
.
Потери на участке A-C равны потерям в 1 трубопроводе или сумме потерь на участке A-B во втором трубопроводе и потерь на участке B-C:
![]() .
.
По условию задачи режим течения в подводящем трубопроводе ламинарный, следовательно, на всех участках режим также ламинарный.
При ламинарном режиме течения потери на трение по длине определяются по формуле Пуазейля:
![]() .
.
Учитывая, что на всех участках трубопровода
диаметр одинаковый, можно записать
![]() .
Выразив потери через соответствующие
длины и расходы, получаем систему из 4
уравнений с 4 неизвестными:
.
Выразив потери через соответствующие
длины и расходы, получаем систему из 4
уравнений с 4 неизвестными:
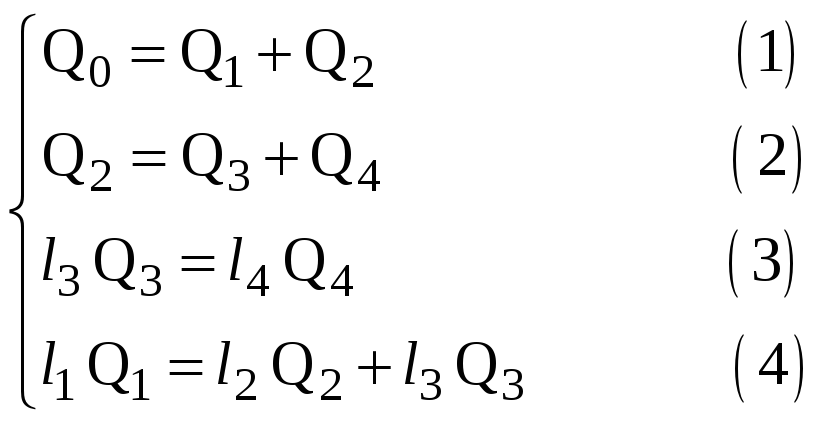
Из (1) получаем
![]() . (5)
. (5)
Подставив (5) в (4), имеем:
![]() или
или
![]() . (6)
. (6)
Из (3) следует, что
![]() .
.
Выразив
![]() в (2) через
в (2) через
![]() ,
имеем:
,
имеем:
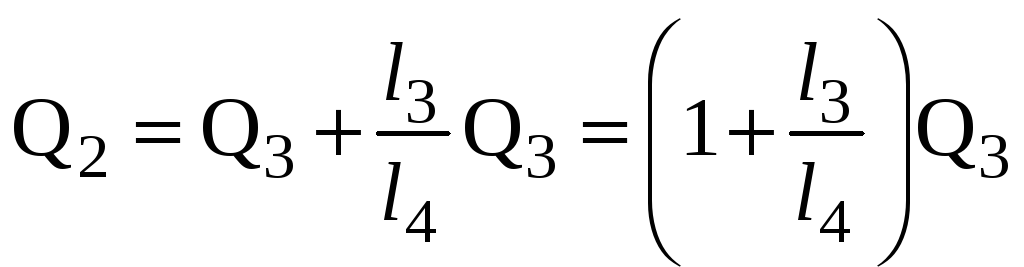 . (7)
. (7)
После подстановки (7) в (6) получим:
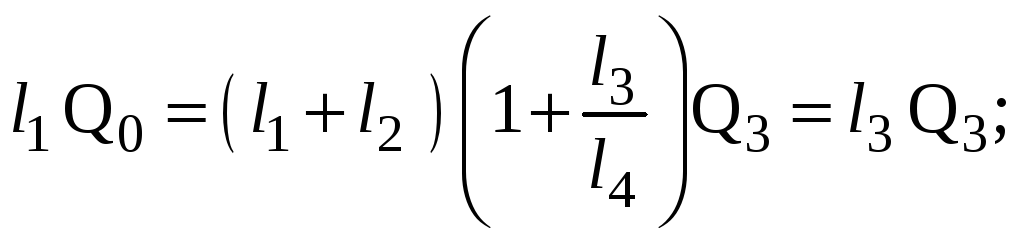
откуда
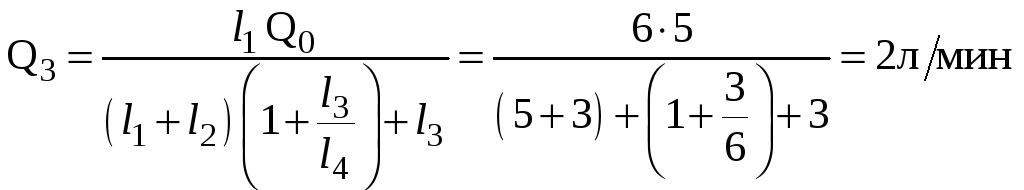 ;
;
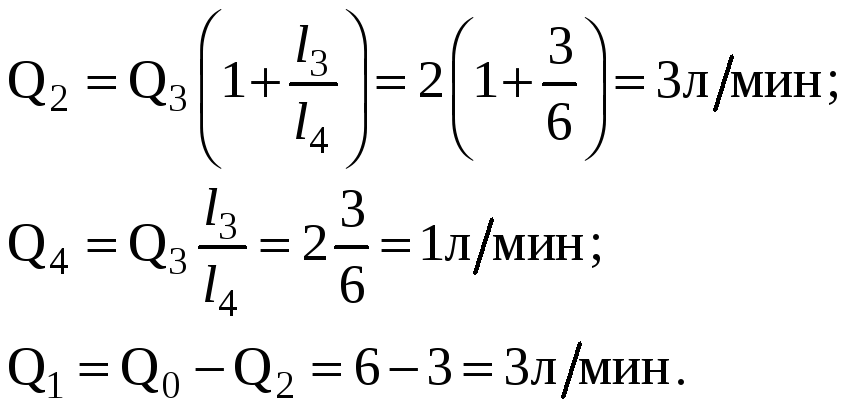
Задача 11.10
Считая жидкость несжимаемой, определить
скорость движения поршня под действием
силы
![]() на штоке.
на штоке.
Диаметр поршня
![]() ,
диаметр штока
,
диаметр штока
![]() .
.
Проходное сечение дросселя
![]() ,
коэффициент расхода
,
коэффициент расхода
![]() ,
избыточное давление слива
,
избыточное давление слива
![]() ,
плотность рабочей жидкости
,
плотность рабочей жидкости
![]() .
.
Всеми сопротивлениями, кроме дросселя, пренебречь.
Д
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() .
.
Найти:
![]() .
.
Р
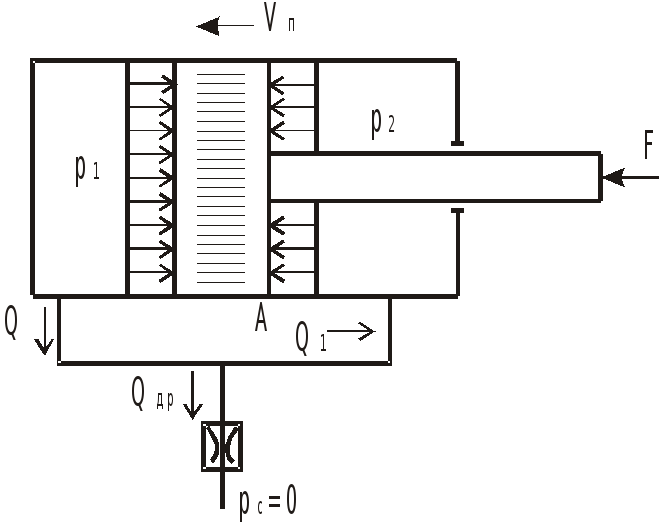
Запишем условие равновесия поршня
![]() .
.
Так как сопротивлением трубопровода пренебрегаем, давления в полостях цилиндра равны:
![]() ,
,
после преобразования получаем:
![]() ;
;
![]() .
.
Через дроссель жидкость вытекает под действием разности давлений:
![]() .
.
Расход через дроссель:
![]() ,
где
,
где
теоретическая скорость:
![]() .
.
Поршень, движущийся со скоростью
![]() ,
вытесняет из левой полости цилиндра
жидкость с расходом
,
вытесняет из левой полости цилиндра
жидкость с расходом
![]() .
В правую полость поступает расход
.
В правую полость поступает расход
![]() .
.
Равенство расходов, подводимых и отводимых от узла A, дает:
![]() или
или
![]() ,
откуда:
,
откуда:
![]() .
.
Искомая скорость поршня:
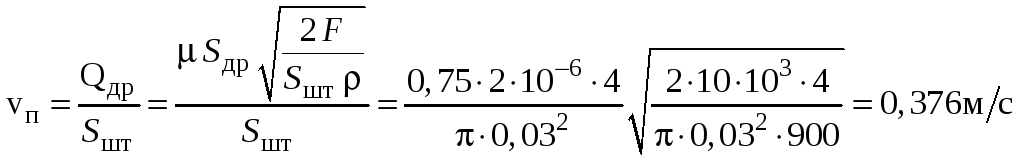 .
.
Ответ:
![]() .
.
Задача 11.11
Правая и левая полости гидроцилиндра сообщаются между собой через дроссель.
О
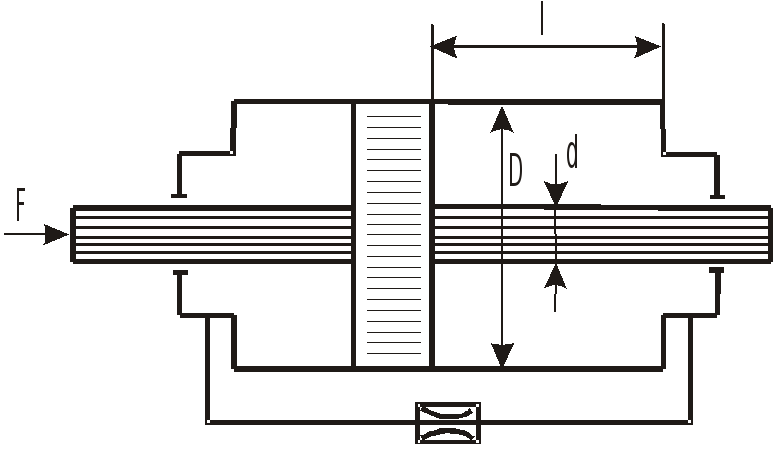
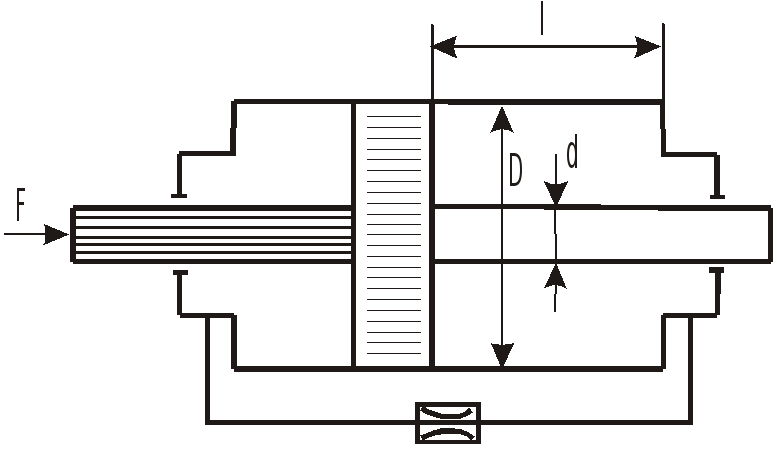
![]() под действием силы
под действием силы
![]() ,
если диаметр поршня
,
если диаметр поршня
![]() ,
диаметр штока
,
диаметр штока
![]() ,
площадь проходного сечения дросселя
,
площадь проходного сечения дросселя
![]() ,
коэффициент расхода
,
коэффициент расхода
![]() ,
плотность жидкости
,
плотность жидкости
![]() .
.
Дано:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Найти: t
Решение:
Под действием силы F в правой полости цилиндра создается давление
![]() .
.
Под действием этого давления жидкость
с расходом
![]() проходит через дроссель:
проходит через дроссель:
![]() .
.
Считая избыточное давление в левой
полости
![]() ,
т.е.
,
т.е.![]() и учитывая, что
и учитывая, что
теоретическая скорость
![]() ;
;
получаем: ![]() .
.
Поршень перемещается вправо со скоростью
![]() и проходит расстояние
и проходит расстояние
![]() за время
за время
![]() .
.
Так как
![]() ,
получаем:
,
получаем:
 .
.
Ответ:
![]() .
.
Задача 11.12
О
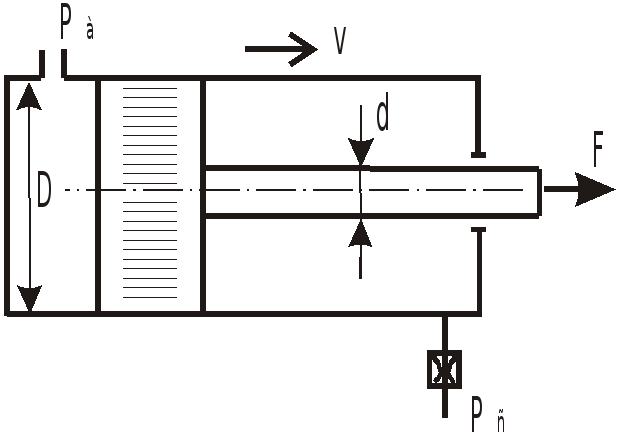
![]() поршень движется со скоростью
поршень движется со скоростью
![]() .
Диаметр штока
.
Диаметр штока
![]() ,
диаметр цилиндра
,
диаметр цилиндра
![]() ,
коэффициент расхода дросселя
,
коэффициент расхода дросселя
![]() ,
плотность жидкости
,
плотность жидкости
![]() ,
давление на сливе
,
давление на сливе
![]() .
.
Дано:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Найти:
![]()
Решение:
Под действием силы
![]() в правой полости цилиндра создается
давление:
в правой полости цилиндра создается
давление:
![]() .
.
Расход жидкости при движении поршня со
скоростью
![]() составит:
составит:
![]() .
.
Через дроссель жидкость проходит под
действием разности давлений
![]() .
.
Теоретическая скорость жидкости в дросселе:
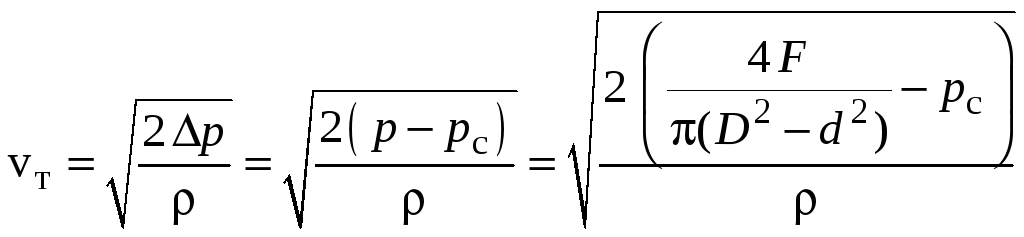 .
.
Расход через дроссель
![]() .
.
Учитывая, что расход жидкости, выходящей из цилиндра, равен расходу через дроссель, находим:

![]() .
.
Ответ:
![]() .
.
З
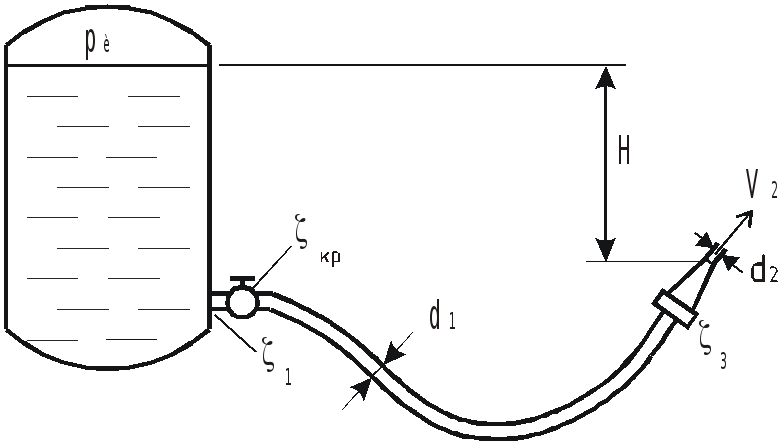
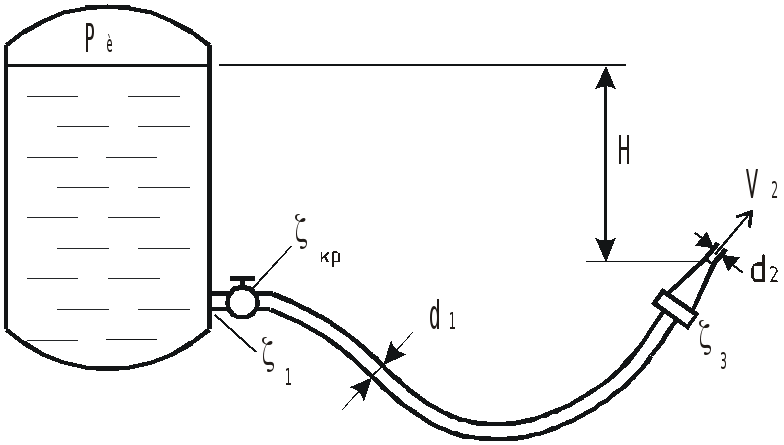
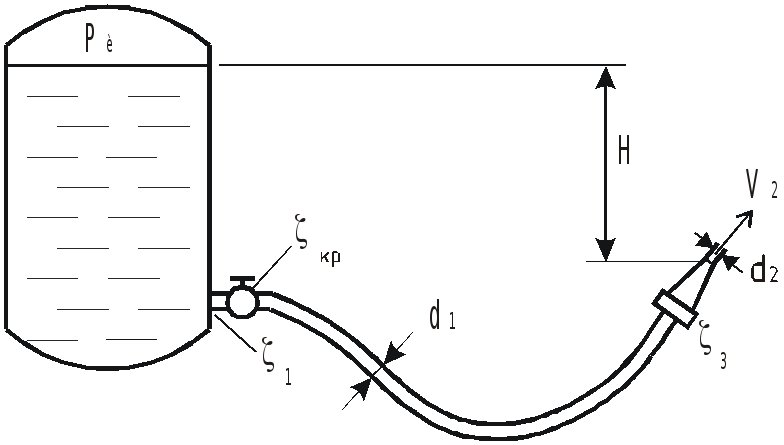
Определить избыточное давление в
напорном баке
![]() ,
необходимое для получения скорости
истечения из брандспойта
,
необходимое для получения скорости
истечения из брандспойта
![]() .
Длина шланга
.
Длина шланга
![]() ,
диаметр
,
диаметр
![]() ,
диаметр выходного отверстия брандспойта
,
диаметр выходного отверстия брандспойта
![]() .
Высота уровня воды в баке над отверстием
брандспойта
.
Высота уровня воды в баке над отверстием
брандспойта
![]() .
Учесть местные гидравлические
сопротивления при входе в трубу
.
Учесть местные гидравлические
сопротивления при входе в трубу
![]() ,
в кране
,
в кране
![]() ,
в брандспойте
,
в брандспойте
![]() .
Шланг считать гидравлически гладким.
.
Шланг считать гидравлически гладким.
Коэффициент вязкости воды
![]() .
.
Ответ:
![]() .
.
З

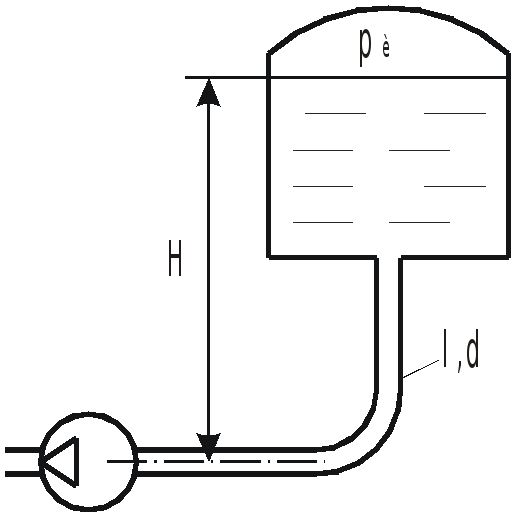
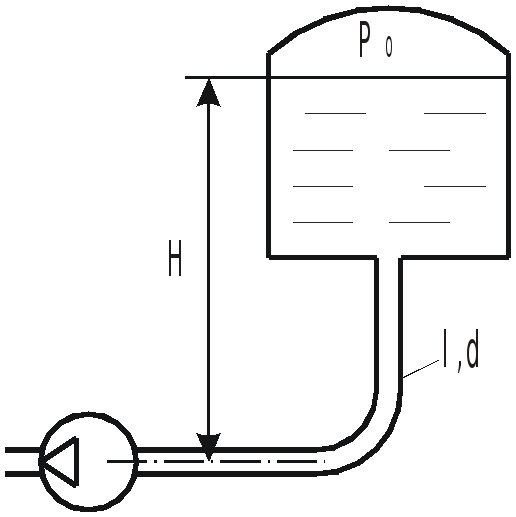
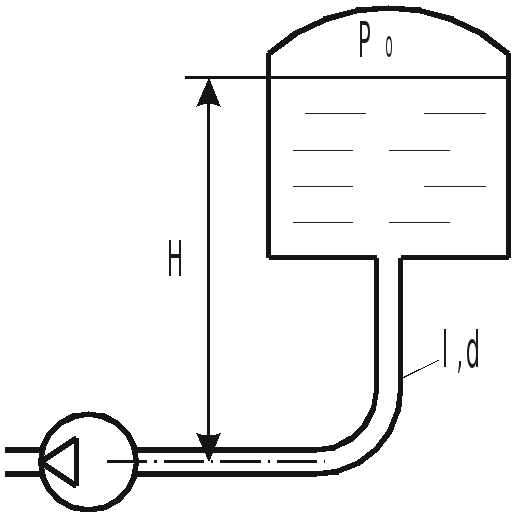
На рисунке показан всасывающий трубопровод
гидросистемы. Длина трубопровода
![]() ,
диаметр
,
диаметр
![]() ,
расход жидкости
,
расход жидкости
![]() .
Абсолютное давление воздуха в баке
.
Абсолютное давление воздуха в баке
![]() ,
,
![]() ,
плотность жидкости
,
плотность жидкости
![]() .
.
Определить абсолютное давление перед
входом в насос при температуре рабочей
жидкости
![]() .
.
Как изменится искомое давление в зимнее
время, когда при этом же расходе
температура жидкости упадет до
![]() .
.
Ответ:
![]() .
.
З
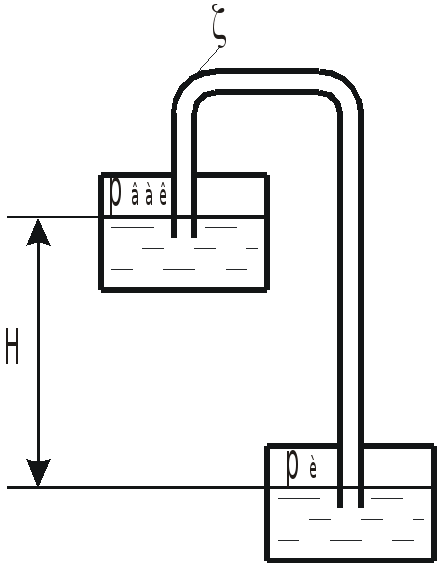
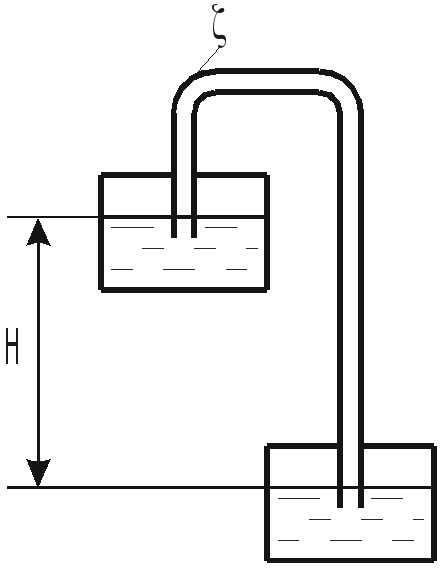
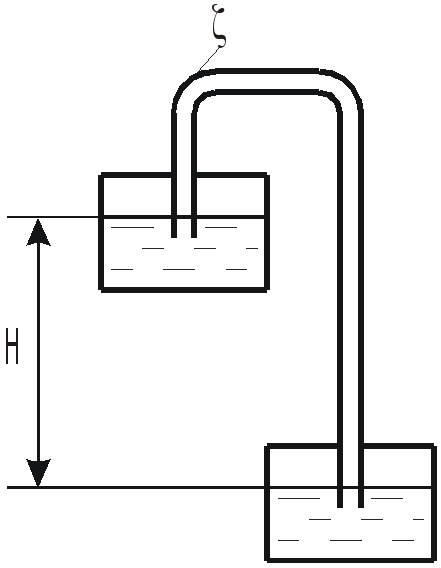
Труба, соединяющая два бака с водой,
имеет длину
![]() и диаметр
и диаметр
![]() ,
и два колена коэффициент сопротивления
каждого из них
,
и два колена коэффициент сопротивления
каждого из них
![]() .
.
Избыточное давление в нижнем баке
![]() ,
вакуум в верхнем баке
,
вакуум в верхнем баке
![]() ,
труба гидравлически гладкая.
,
труба гидравлически гладкая.
Определить, при какой высоте
![]() жидкость будет двигаться из верхнего
бака в нижний с расходом
жидкость будет двигаться из верхнего
бака в нижний с расходом
![]() ,
а при какой высоте
,
а при какой высоте
![]() будет двигаться в обратном направлении
с тем же расходом.
будет двигаться в обратном направлении
с тем же расходом.
О
![]() .
.
Задача 11.16
Определить минимально возможный диаметр
всасывающего трубопровода, если подача
насоса
![]() ,
высота всасывания
,
высота всасывания
![]() ;
длина трубопровода
;
длина трубопровода
![]() ,
шероховатость трубы
,
шероховатость трубы
![]() .
Коэффициент сопротивления входного
фильтра
.
Коэффициент сопротивления входного
фильтра
![]() ;
максимально допустимый вакуум на входе
в насос
;
максимально допустимый вакуум на входе
в насос
![]() ,
вязкость рабочей жидкости
,
вязкость рабочей жидкости
![]() ,
плотность
,
плотность
![]() .
.
Ответ:
![]() .
.
З
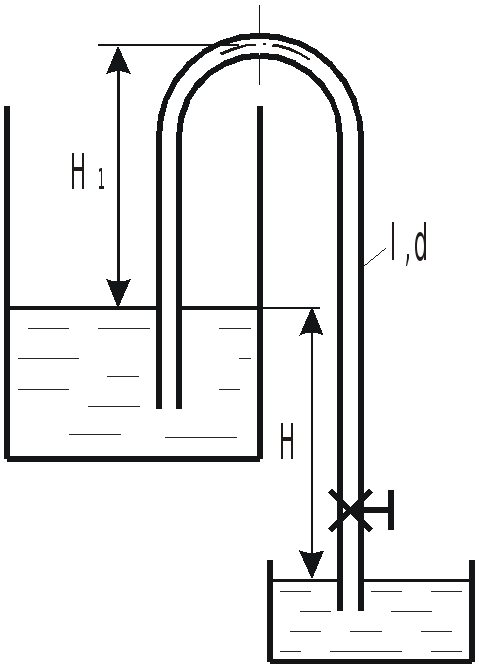
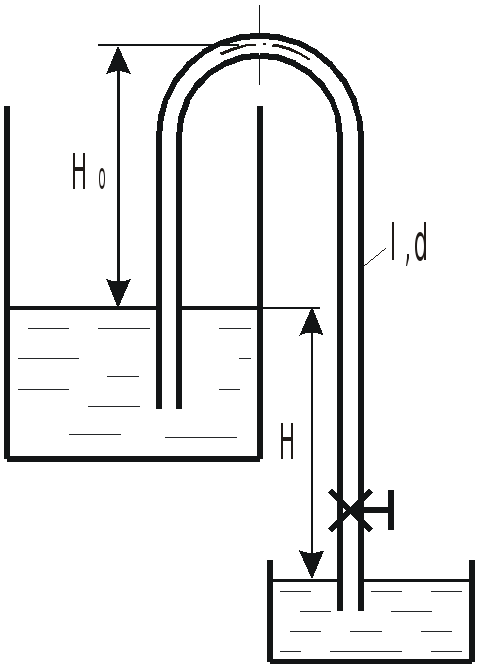
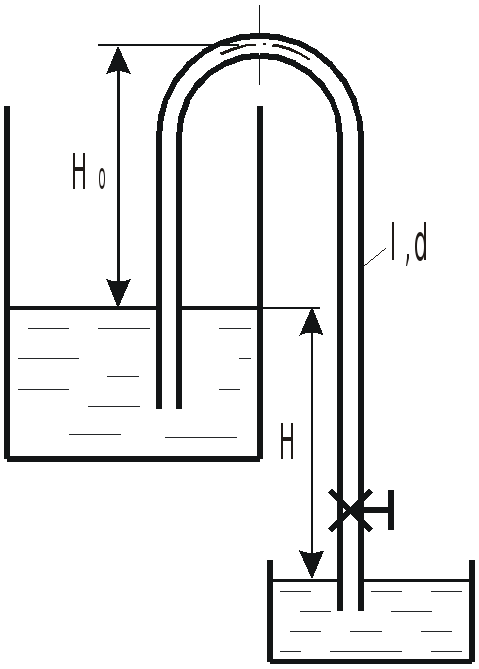
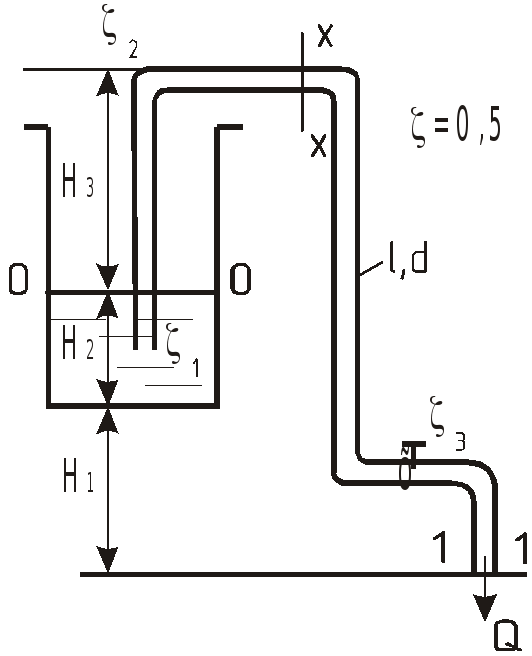
Определить расход воды через сифонный
трубопровод, изображенный на рисунке,
если
![]() ,
общая длина трубы
,
общая длина трубы
![]() ,
диаметр
,
диаметр
![]() .
.
Учесть потери на входе и выходе и в
вентиле
![]() и на трение в трубе (принять
и на трение в трубе (принять
![]() ).
).
Подсчитать вакуум в верхнем сечении
трубы
![]() ,
если длина участка от входа в трубу до
этого сечения
,
если длина участка от входа в трубу до
этого сечения
![]() .
.
Ответ:
![]() ;
абсолютное давление
;
абсолютное давление
![]() .
.
З
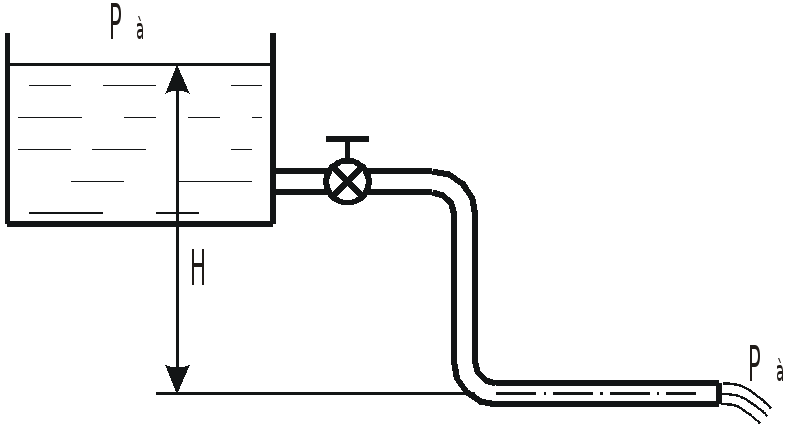
Определить расход воды
![]() ,
вытекающий из бака, если диаметр трубы
,
вытекающий из бака, если диаметр трубы
![]() ,
длина
,
длина
![]() ,
высота
,
высота
![]() ,
коэффициент сопротивления крана
,
коэффициент сопротивления крана
![]() ,
колена
,
колена
![]() ,
шероховатость трубы
,
шероховатость трубы
![]() .
.
Ответ:
![]() .
.
З
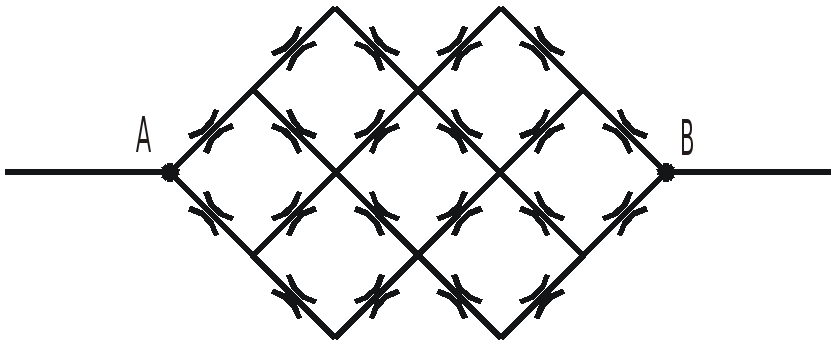
Двадцать одинаковых дросселей соединены в гидравлическую цепь, расположенную в горизонтальной плоскости так, как показано на рисунке.
Гидравлические потери на одном дросселе
при расходе
![]() составляют
составляют
![]() .
.
Определить гидравлические потери между
точками A и B
при том же расходе
![]() ,
подводимом к гидравлической сети.
,
подводимом к гидравлической сети.
Потерями на трение по длине, на слияние и разделение потока пренебречь. Течение в области квадратичного сопротивления.
Указание: Прямой AB следует рассечь систему на две симметричные и независимые подсистемы. Далее принцип симметрии применить и к другим разветвлениям.
Ответ:
![]() .
.
Задача 11.20
О
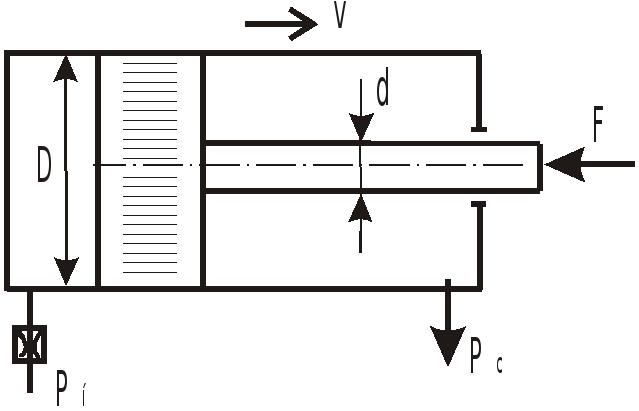
![]() ,
преодолеваемой штоком гидроцилиндра
при движении его против нагрузки со
скоростью
,
преодолеваемой штоком гидроцилиндра
при движении его против нагрузки со
скоростью
![]() .
.
Давление на входе в дроссель
![]() ,
давление на сливе
,
давление на сливе
![]() .
.
Коэффициент расхода дросселя
![]() ,
диаметр отверстия дросселя
,
диаметр отверстия дросселя
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Ответ:
![]() .
.
