Раздел 11. Гидравлический расчет трубопроводов Простой трубопровод.

Простым называется трубопровод постоянного поперечного сечения, произвольно расположенный в пространстве и содержащий ряд местных сопротивлений.

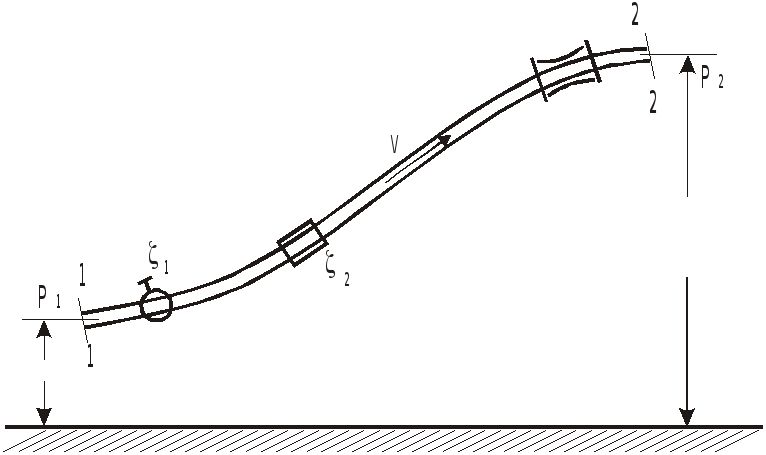
Схема простого трубопровода

Запишем уравнение Бернулли для сечений 1-1—2-2.

или

.

Пьезометрическая высота - это удельная потенциальная энергия, которой обладала жидкость в сечении 1-1, и которая была израсходована на подъем жидкости на , создание в сечении 2-2 давления и преодоление сопротивления в трубопроводе. Сумма - это потенциальная энергия, которой обладает жидкость в сечении 2-2.

Таким образом, разность потенциальных энергий ушла на компенсацию потерь:

.

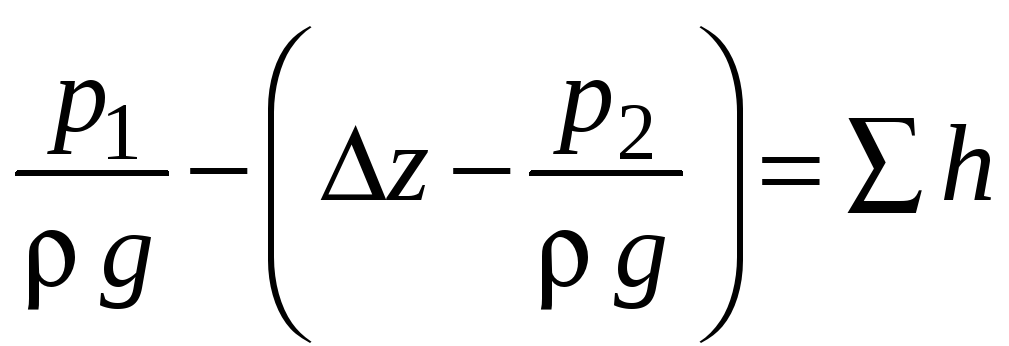Левую часть можно представить как высоту подъема жидкости (статический напор) .

Если величина задана по условиям задачи, то будем называть ее – располагаемым напором ; если ее нужно определить, то в общем случае будем обозначать напор, расходуемый на преодоление сопротивления .

.

Потери напора на преодоление сопротивления складываются из потерь по длине и местных потерь.

.

В общем случае потери зависят от расхода , а значение показателя степени зависит от режима течения жидкости.

При ламинарном режиме течения потери в местных сопротивлениях можно заменить потерями в трубопроводе длиной при условии, что , т.е. , откуда эквивалентная длина трубопровода:

,

(11.1)

или , т.е. .

Для турбулентного режима:

,

или выражая скорость через расход, получим:

.

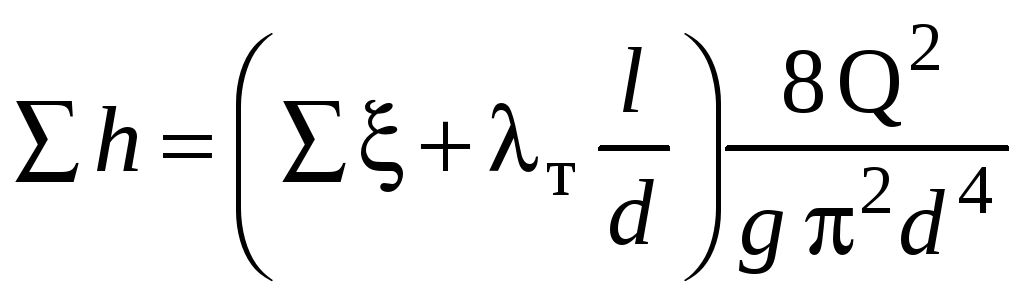Следовательно .

Необходимо помнить, что коэффициент потерь также зависит от , а следовательно и от расхода .

В зависимости от того, какие из величин необходимо определить в результате гидравлического расчета, различают несколько расчетных случаев.

1. Определение потребного напора .

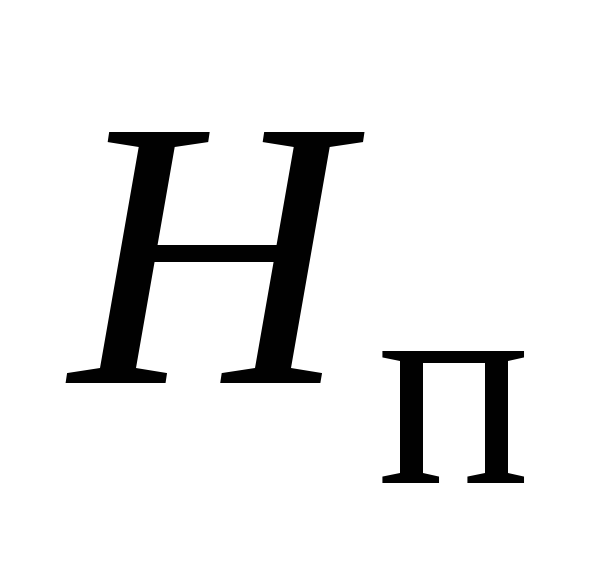Считаются заданными:

• - плотность жидкости;

• - кинематический коэффициент вязкости;

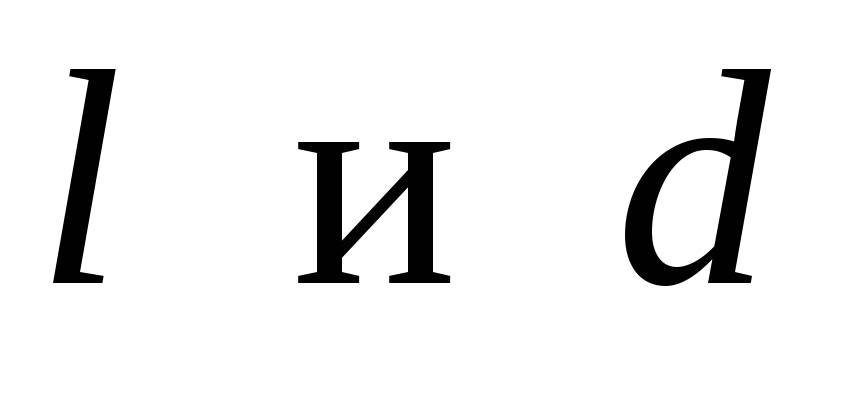• - длина и диаметр трубопровода;

• - относительная шероховатость трубы;

• - коэффициенты местных сопротивлений.

Порядок расчета:

По известным значениям расхода , диаметра и вязкости определяем критерий Рейнольдса ; по и определяем зону сопротивления (т.е. зависимость, по которой определяется коэффициент трения ) и вычисляем потребный напор . Схематически порядок расчета можно представить в виде:

.

2. Определение диаметра трубопровода .

Заданы: и располагаемый напор .

Для ламинарного режима течения диаметр можно определить, выразив его из зависимости (11.1):

.

Для турбулентного режима однозначно решить задачу невозможно, так как для определения коэффициента трения необходимо знать , а для вычисления должен быть известен диаметр .

Задачу решаем методом последовательных приближений.

Задаемся значением диаметра , после чего задача определения сводится к 1 расчетному случаю:

.

Сравниваем полученное значение с располагаемым напором .

Если оказывается, что , то необходимо во втором приближении выбрать и повторить расчет.

В случае, если , диаметр следующего приближения выбирается из условия , обычно достаточно бывает сделать 3-4 приближения.

По полученным данным нужно построить график зависимости , по заданному располагаемому напору найти по графику значения диаметра и выбрать ближайший больший стандартный диаметр.

Значком отмечены стандартные размеры труб

Зависимость потерь в трубопроводе от диаметра d

3. Определение расхода .

Заданными считаются все параметры кроме расхода.

Для ламинарного режима течения расход можно определить, выразив из (11.1).

.

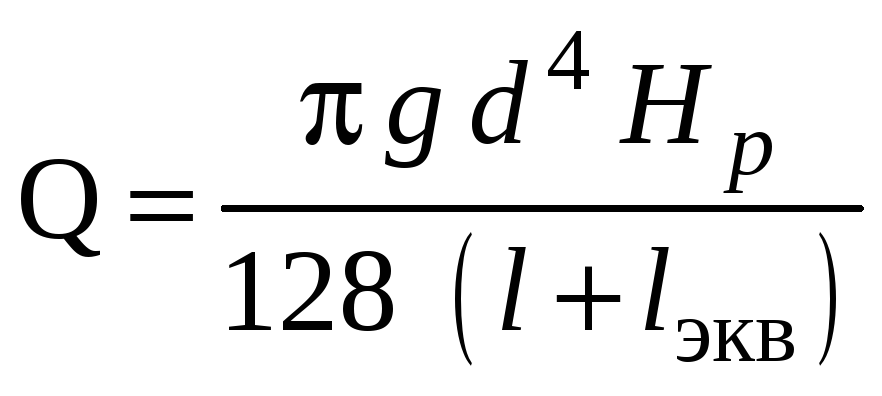Для турбулентного течения эту задачу также приходится решать методом последовательных приближений.

Напор, потребный для преодоления гидравлического сопротивления, определяется из соотношения:

;

откуда .

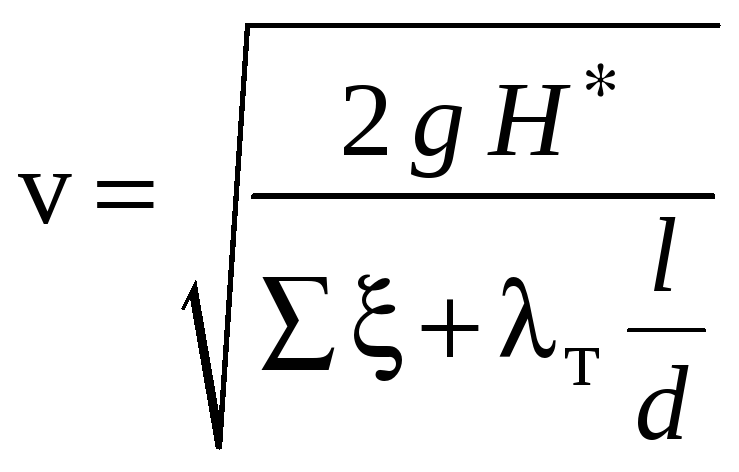При отсутствии вязкости (жидкость идеальная) теоретическая скорость, с которой может двигаться жидкость в трубопроводе, определяется как

.

Отношение действительной скорости к теоретической называется коэффициентом скорости .

Для простого трубопровода

.

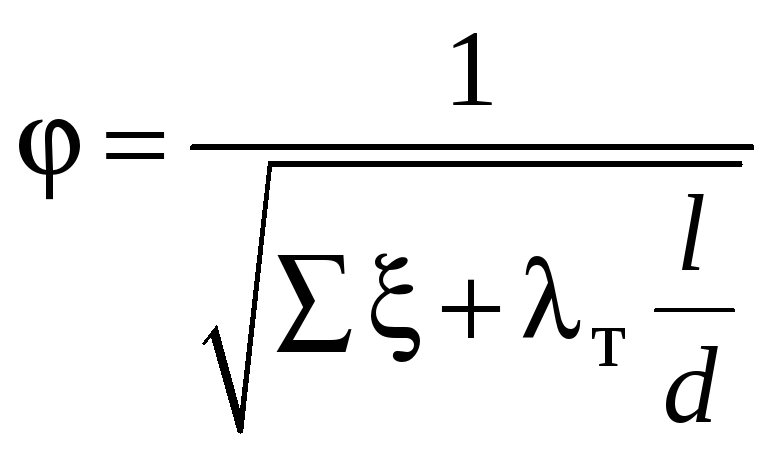Учитывая, что значение коэффициента трения для турбулентного режима течения в большинстве расчетных случаев укладывается в диапазон , выбираем значение - первого приближения из этого диапазона и, определив , вычисляем , уточняем значение критерия , определяем и . Схематически это можно изобразить следующим образом:

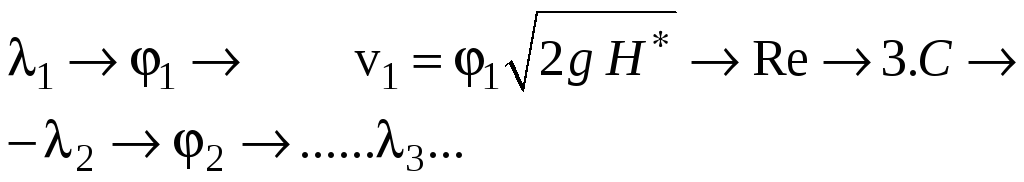
Расчет заканчивается после выполнения условия:

, где - наперед заданная точность в %.

Обычно достаточно бывает трех приближений.

При отсутствии опыта в выборе значения можно принимать в первом приближении .

При истечении в атмосферу следует учитывать еще и потери на выходе из трубы.

При большом объеме расчетных работ удобней использовать графический метод определения расхода. Для этого, задавшись рядом значений расходов или скорости , определим соответствующие значения потребных напоров. По полученным данным строим характеристику трубопровода (график зависимости или ) и по известному значению находим расход .

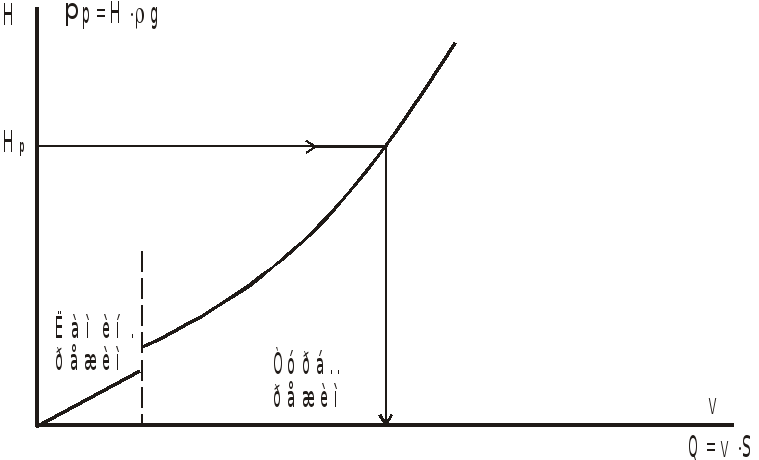
Характеристика трубопровода

Сифон.

С

ифоном называется такой простой самотечный трубопровод, часть которого расположена выше питающего его резервуара.

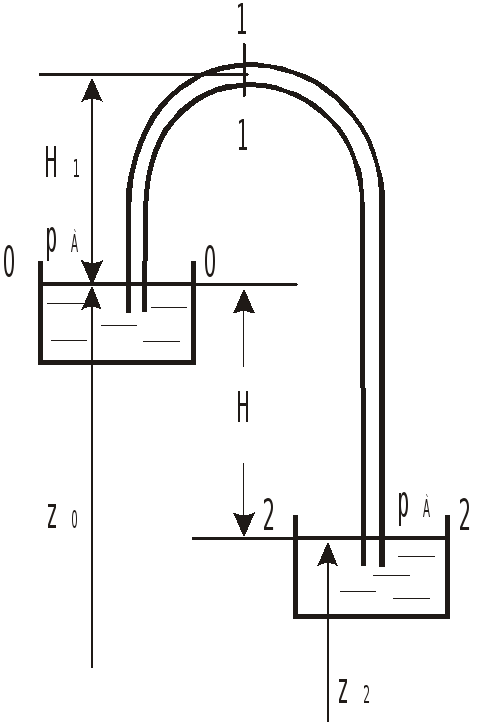
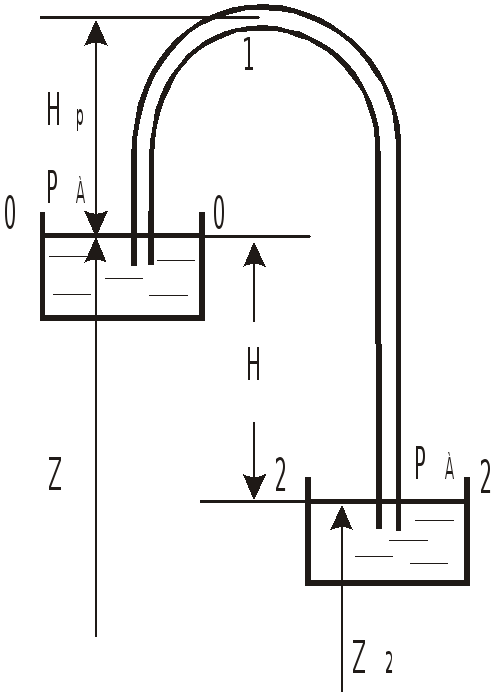
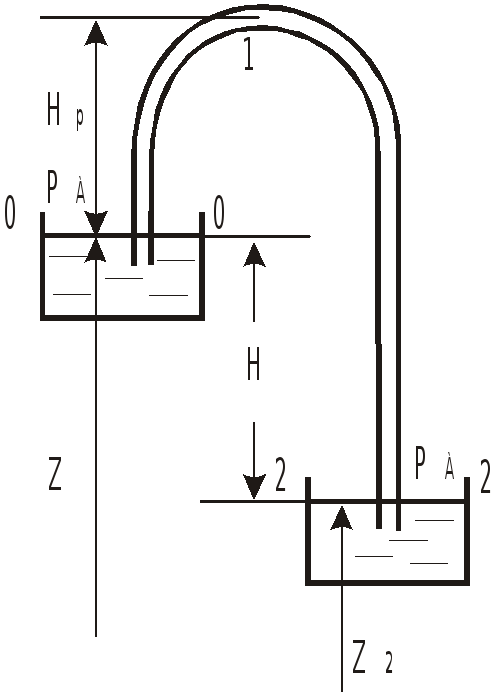
Запишем уравнение Бернулли для сечений 0-0—2-2

или

,

т.е. расход жидкости зависит только от разности уровней и не зависит от - высоты подъема над верхним резервуаром.

Но это справедливо лишь до тех пор, пока с увеличением высоты давление в верхней точке (сечение 1-1) не уменьшится до давления упругости паров жидкости, что вызовет образование паровой пробки и, как следствие, прекращение подачи жидкости.

Если известен расход жидкости через сифон и размеры трубопровода, то абсолютное давление может быть найдено из уравнения Бернулли для сечений 0-0—1-1.

.

Если известно минимально допустимое давление , то, зная расход, можно из того же уравнения найти максимально допустимую высоту .