Раздел 10. Истечение жидкости через отверстия и насадки

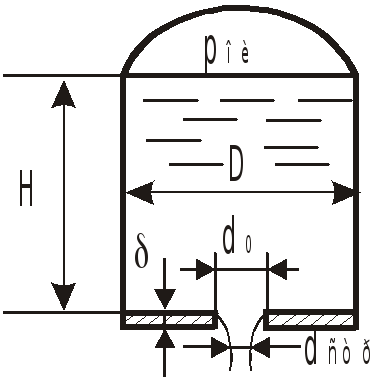
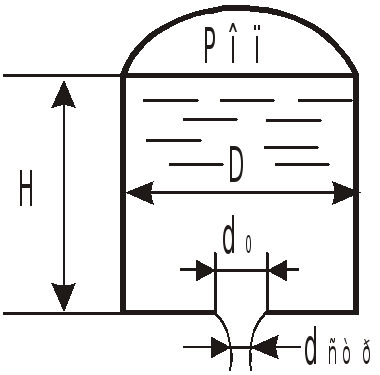
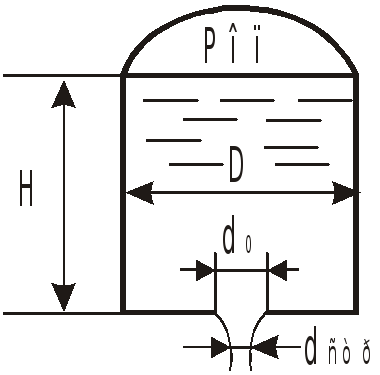
1. Истечение через отверстия

З

акономерности истечения жидкости из отверстия с острой кромкой в тонкой стенке одинаковы, как для цилиндрических отверстий, так и для конических расширяющихся отверстий, лишь бы входная кромка не была скруглена и толщина стенки не превышала бы критического значения, при котором струя коснется стенки и .

Истечение жидкости может происходить либо в газовую среду, например в атмосферный воздух, либо в среду той же жидкости. В последнем случае вся кинетическая энергия струи теряется на вихреобразование.

Из-за непараллельности линий тока на входе в отверстие площадью струя сужается и на расстоянии площадь сечения струи становится минимальной.

Сужение струи характеризуется коэффициентом сужения .

Теоретическая скорость истечения (без учета потерь на входе в отверстие) , где - удельная потенциальная энергия.

Теоретический расход .

Действительные значения скорости и расхода отличаются от теоретических и характеризуются коэффициентами скорости и расхода .

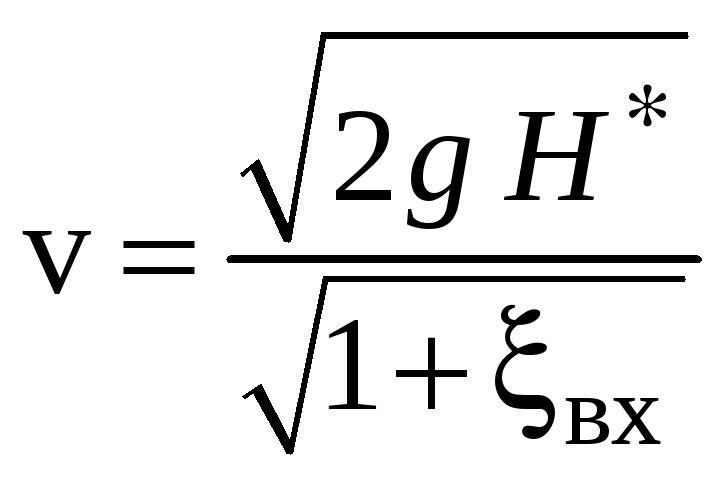Действительная скорость меньше теоретической из-за потерь на входе в отверстие , где - коэффициент потерь на входе в отверстие.

Действительный расход меньше теоретического не только из-за уменьшения действительной скорости, но и из-за сужения струи. Выражая через теоретическое значение скорости и площадь отверстия, получим:

;

т.е. .

При истечении через отверстие в боковой стенке закономерности остаются такими же, если и отверстие достаточно далеко отстоит от дна.

2. И стечение через насадки

Н

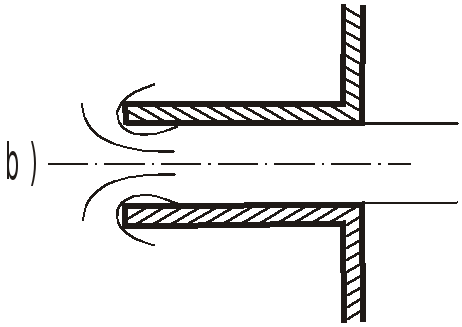
асадком называется короткая трубка, через которую жидкость вытекает из емкости. Наиболее распространены цилиндрические насадки – внешний (а) и внутренний (b).

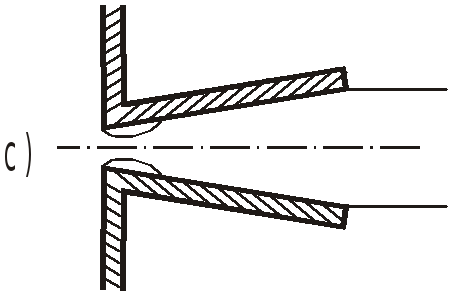
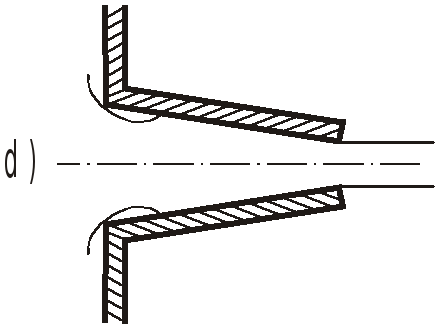
Применяются также насадки конические – расширяющийся (c) и сужающийся (d).

П

ри входе в насадок струя сужается, а затем постепенно расширяясь, заполняет все поперечное сечение насадка.

П

оэтому коэффициент сжатия, равный отношению площади струи к площади на выходе из насадка .

Коэффициенты истечения зависят от числа Рейнольдса и определяются опытным путем.

При значении коэффициенты истечения остаются постоянными.

Значения коэффициентов истечения через отверстие и насадки, приведены в таблице.

№	Тип насадка
1.	Отверстие в тонкой стенке	0,61	0,97	0,62	0,065
2.	Внешний цилиндрический	1	0,82	0,82	0,5
3.	Внутренний цилиндрический	1	0,71	0,71	0,98
4.	Конический сходящийся	0,83	0,961	0,946	0,083
5.	Конический расходящийся	1	0,45	0,45	3,9

3. Определение коэффициентов истечения опытным путем.

Четыре коэффициента истечения связаны двумя зависимостями.

Таким образом, достаточно опытным путем определить два из них, а оставшиеся определить из соотношений:

или и .

Задача 10.1

При исследовании истечения из круглого отверстия диаметром из опыта получено .

П

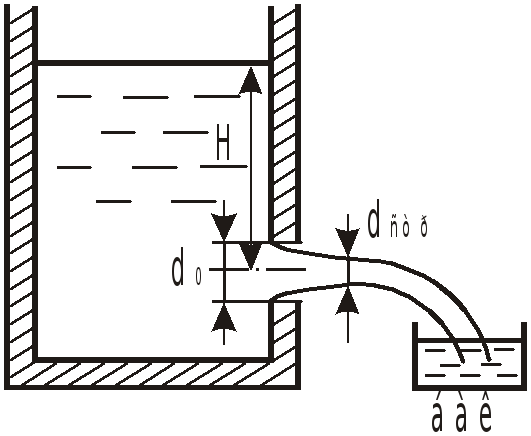
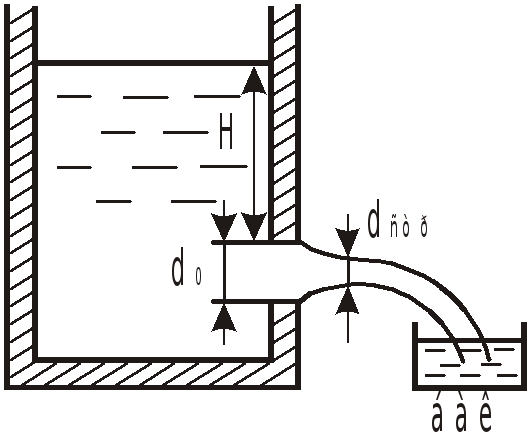
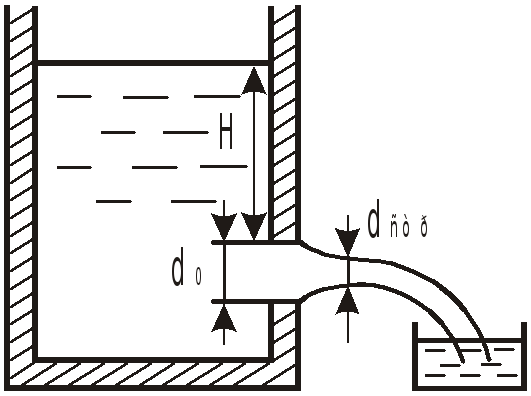
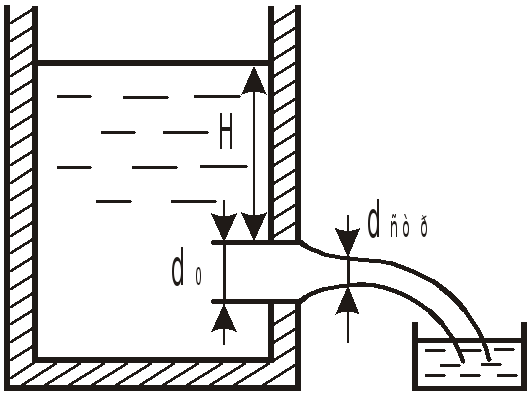
ри напоре бак объемом был заполнен за 32,8 сек.

Определить коэффициент истечения .

Решение.

Коэффициент сжатия .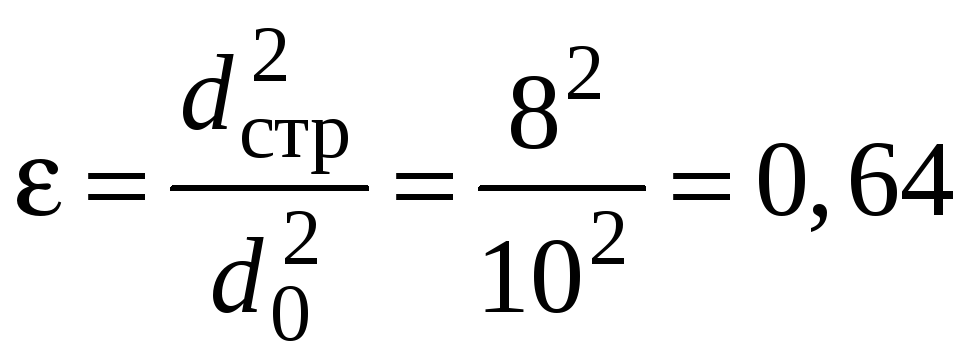

Теоретический расход:

Действительный расход .

Коэффициент расхода .

Коэффициент скорости .

Коэффициент потерь .

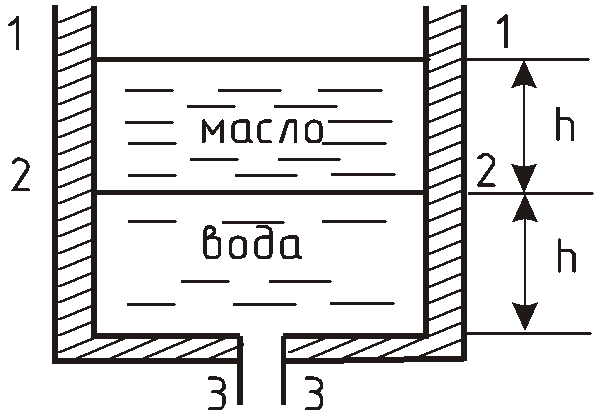
Задача 10.2

О

пределить начальную скорость истечения жидкости из сосуда через отверстие в тонкой стенке в случаях:

1. Сосуд заполнен слоями воды и масла 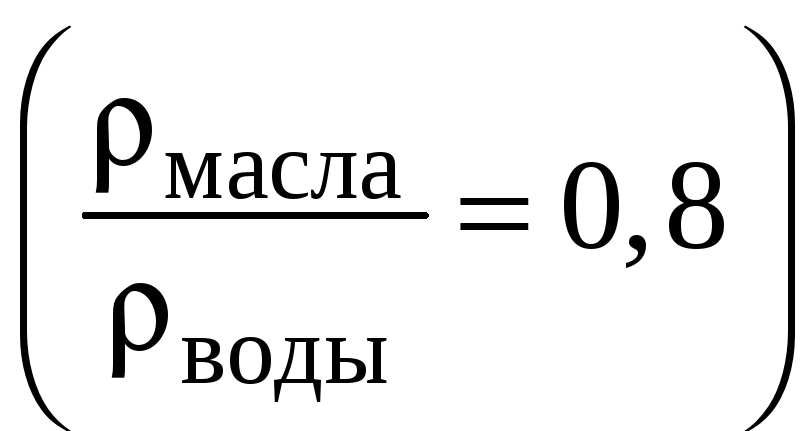одинаковой высоты .

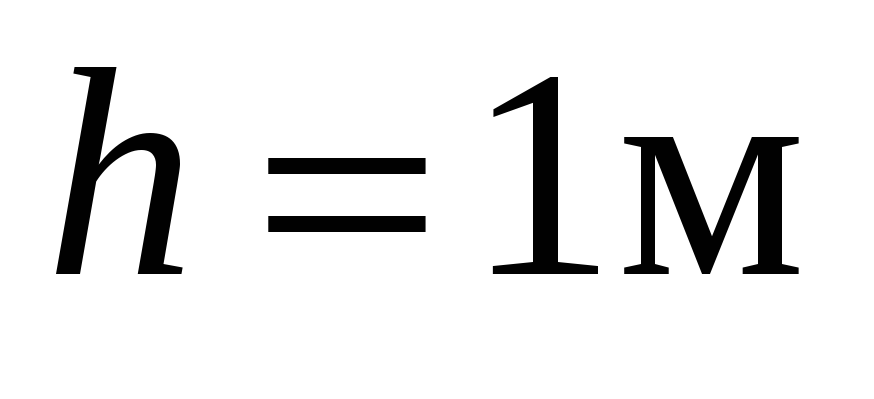2. Сосуд заполнен до уровня 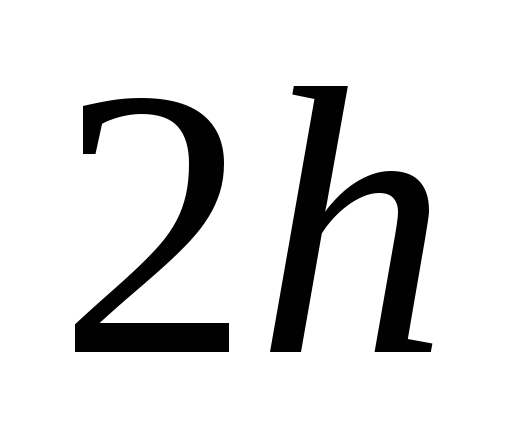только водой или только маслом.

Решение:

1. Уравнение Бернулли справедливо только для потока одной и той же жидкости, поэтому выбираем сечения 2-2—3-3.

2. Без учета потерь:

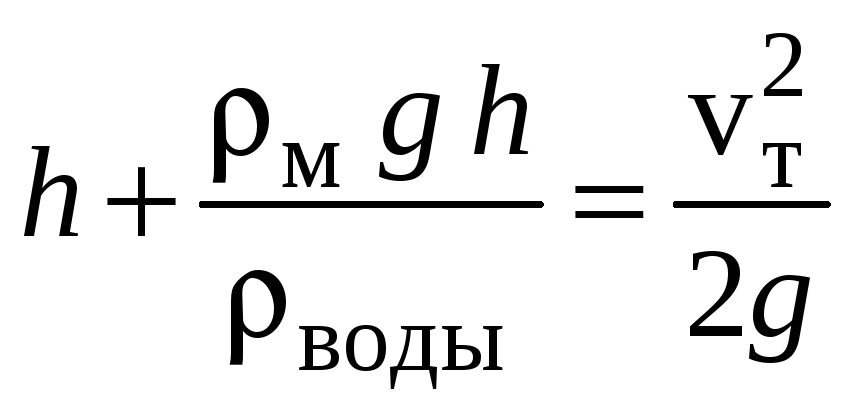, откуда теоретическая скорость:

.

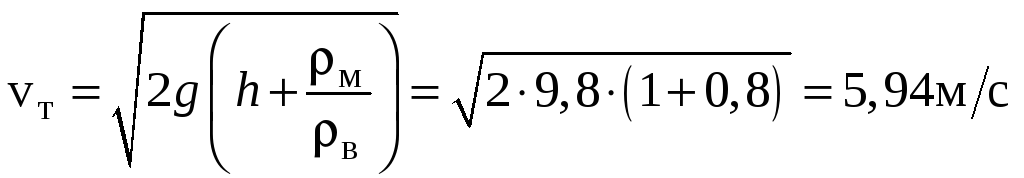Действительная скорость .

2. 1-1—3-3

; ;

.

Можно было записывать уравнение Бернулли для реальной жидкости.

1-1—3-3

На входе в отверстие скорости во всех точках сечения одинаковы, следовательно .

.

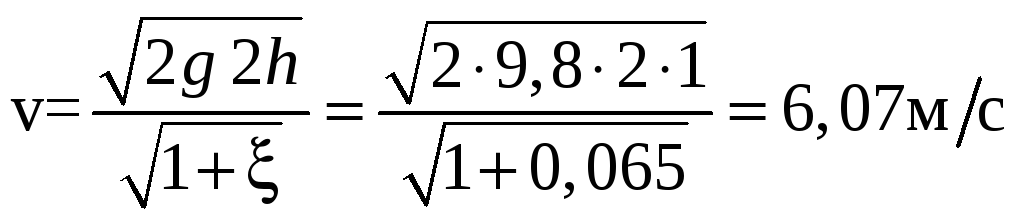З

адача 10.3

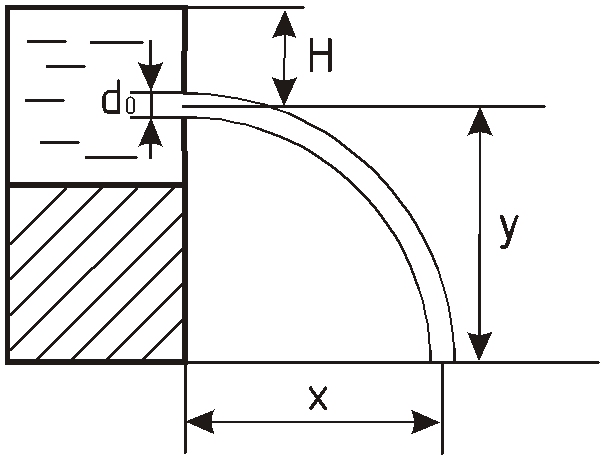
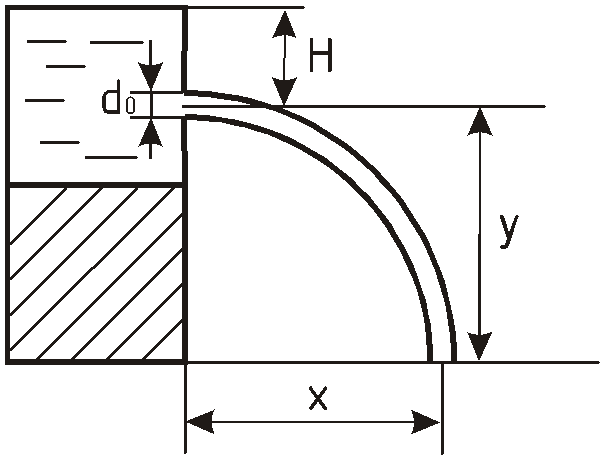
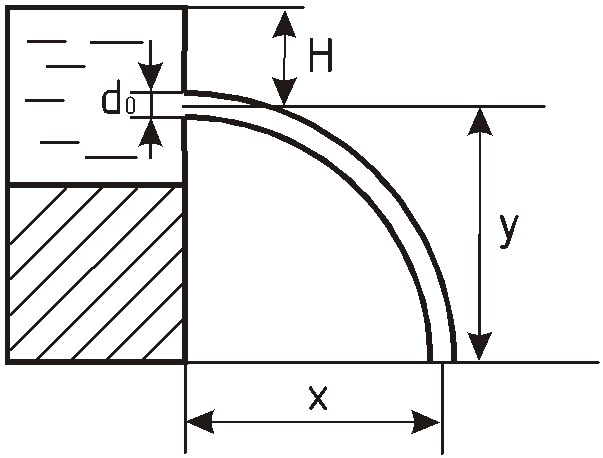
При истечении через отверстие диаметром измерены , , , расход жидкости .

Подсчитать значение коэффициентов .

Сопротивлением воздуха пренебречь.

Решение.

После выхода из отверстия частица жидкости участвует в равномерном движении со скоростью в горизонтальном направлении и равномерноускоренном, с начальной скоростью, равной нулю, в вертикальном.

Поэтому и , исключая , находим , учитывая, что , находим коэффициент скорости .

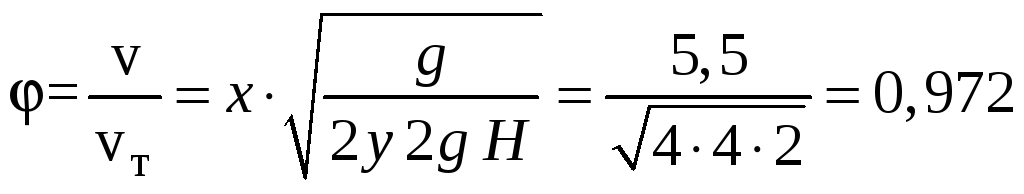Теоретический расход:

.

Коэффициент расхода: .

Коэффициент сжатия: .

Коэффициент потерь: .

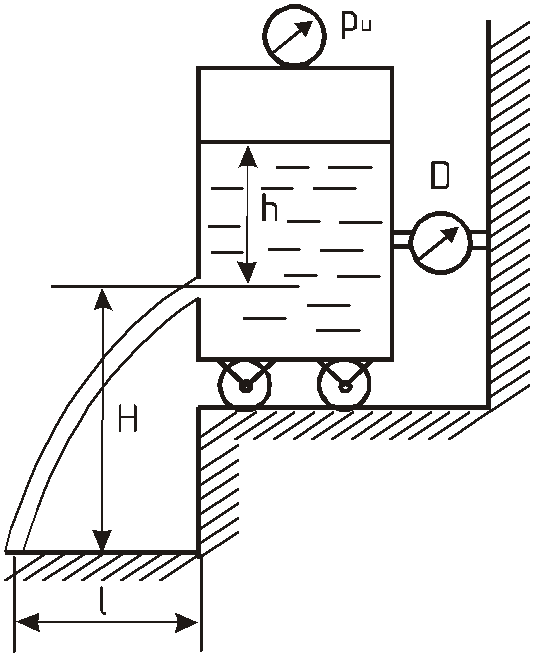
Задача 10.4

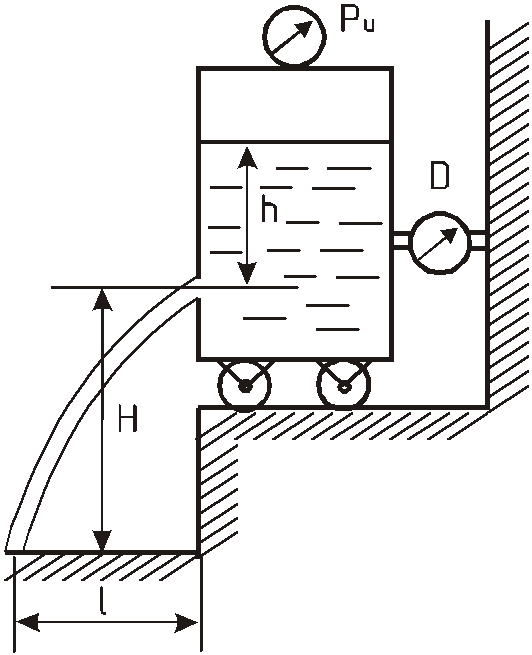
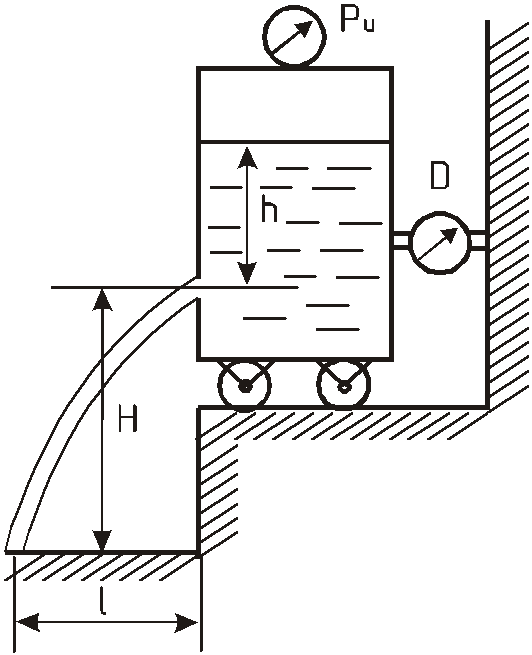
На рисунке показана схема установки для исследования истечения через отверстия и насадки.

Резервуар с водой имеет возможность скользить по основанию практически без трения.

При истечении сила реакции струи измеряется с помощью динамометра и равна .

Подсчитать коэффициенты истечения , если площадь отверстия , избыточное давление , , , .

Д

ано:

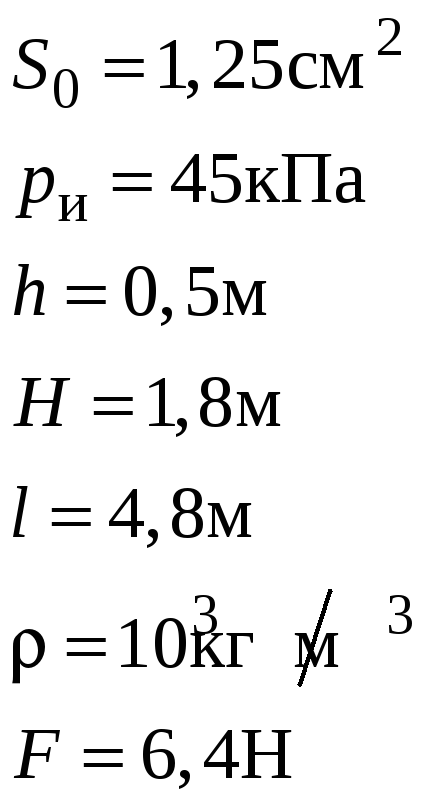
Найти: .

Решение.

Теоретическая скорость истечения:

.

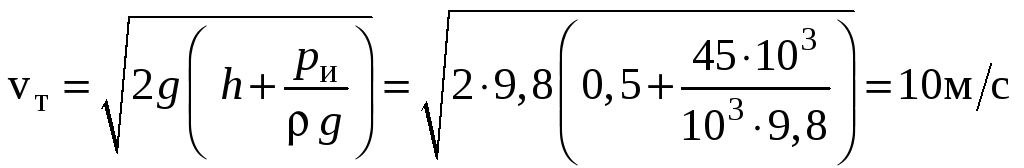Действительная скорость (см. задачу. 10.3):

.

Коэффициент скорости:

.

Воспользуемся теоремой ”Приращение количества движения равно импульсу внешней силы”:

; учитывая, что , получаем:

;

откуда .

Коэффициент сжатия струи: .

Коэффициент расхода: .

Коэффициент потерь: .

З

адача 10.5

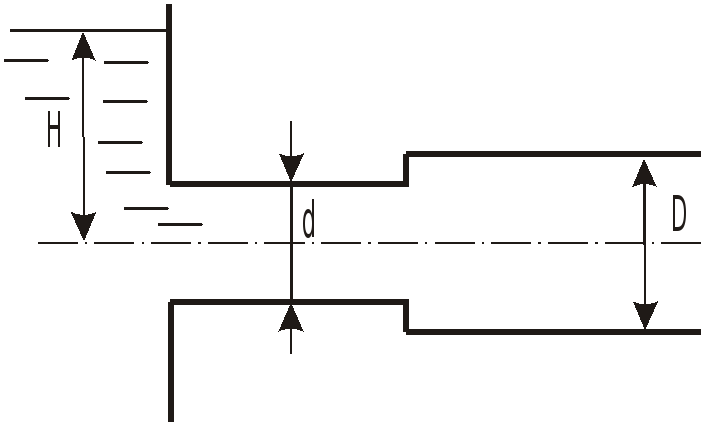
1. Для насадка, составленного из двух цилиндрических патрубков диаметрами

и , определить коэффициенты потерь и расхода .

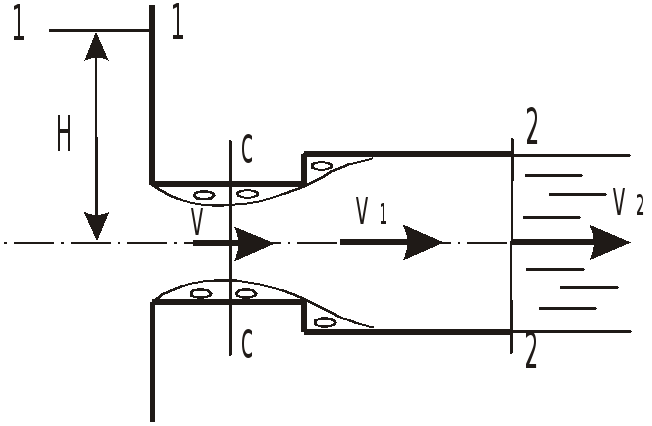
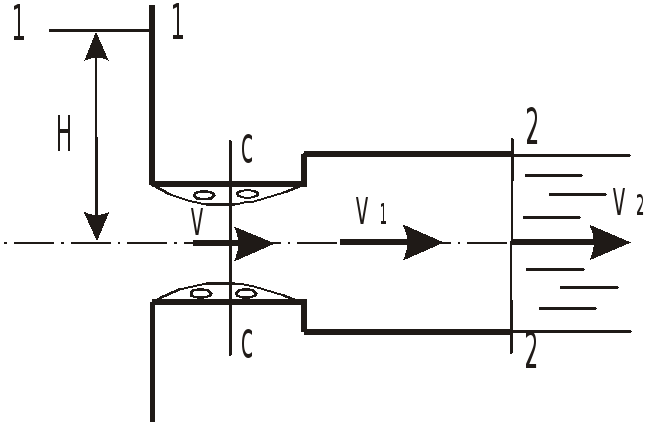
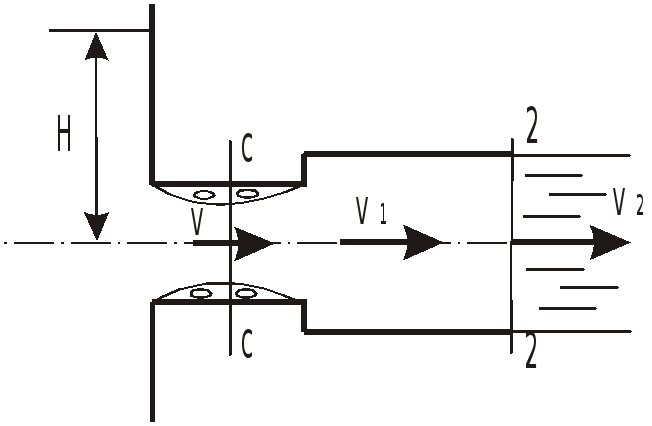
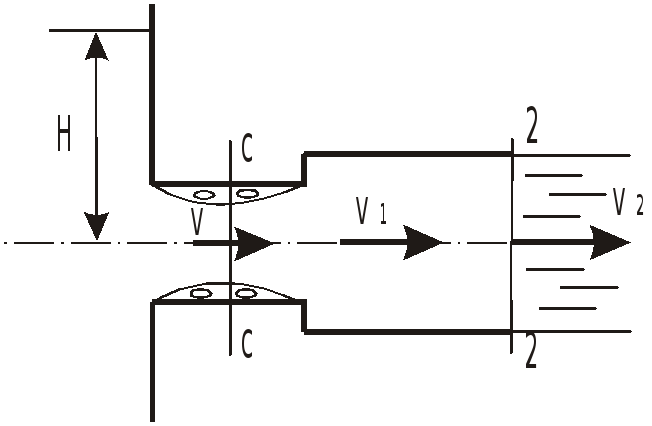
2. Найти предельный напор 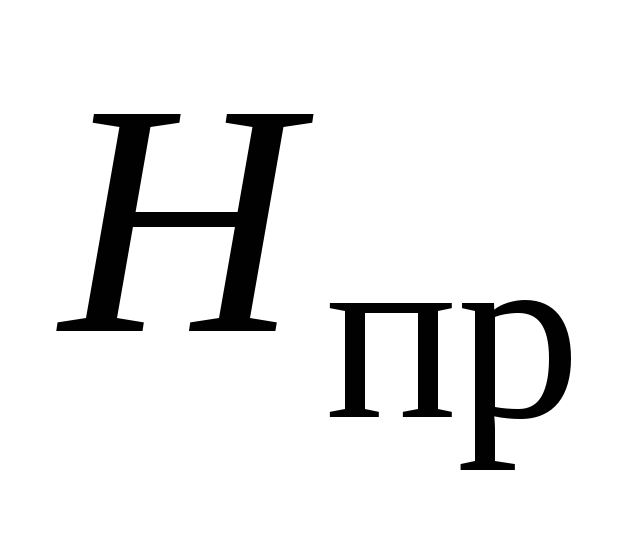в случае истечения воды в атмосферу, принимая, что при 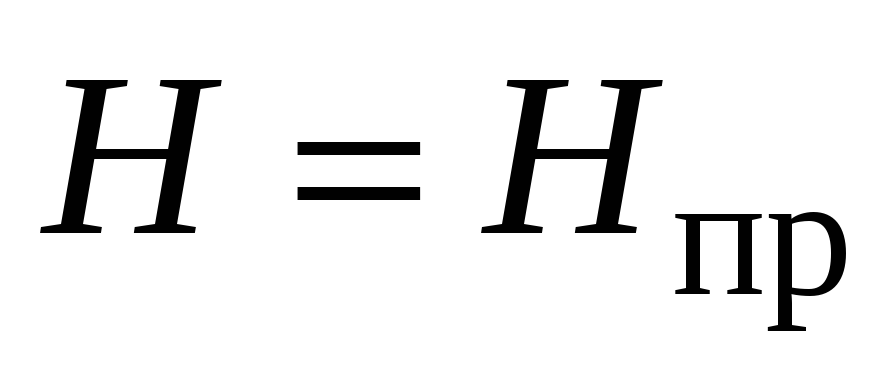вакуумметрическая высота в наименьшем сечении потока достигает .

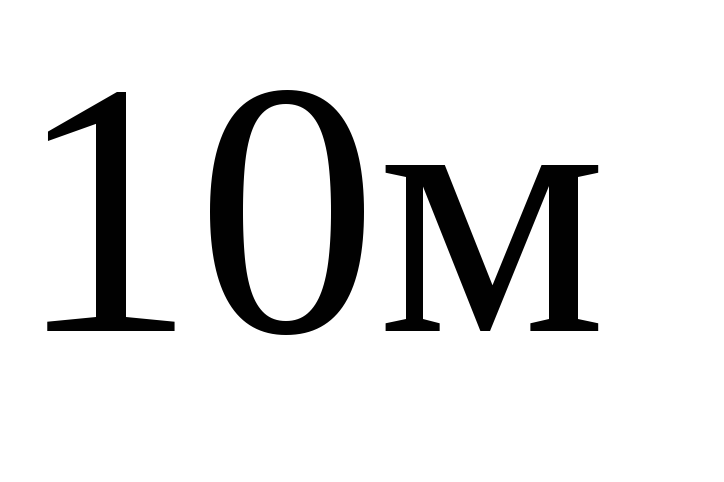К

оэффициент сжатия струи в узком сечении принять равным .

Решение:

Предположим, что режим турбулентный, тогда

для сечений 1-1—2-2 имеем:

.

Потери в составном насадке складываются из потерь в насадке с и потерь на внезапное расширение потока от до :

.

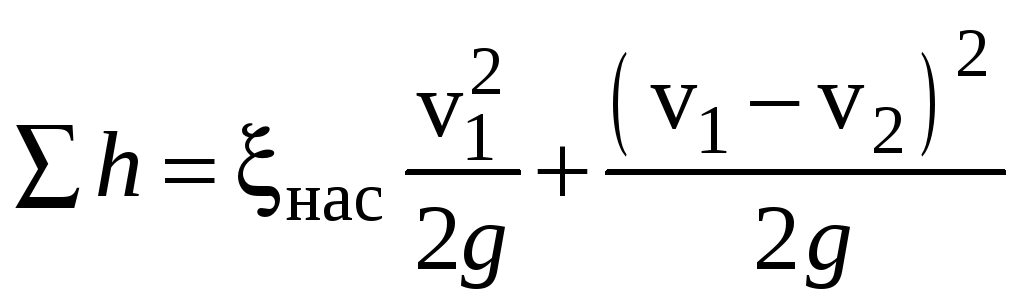Выразив из уравнения расхода скорость ,

получаем: ;

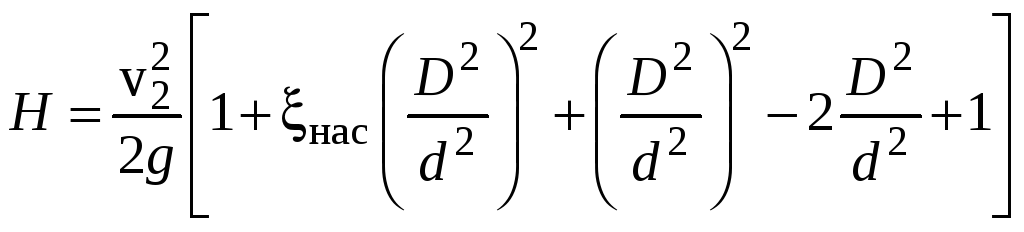откуда .

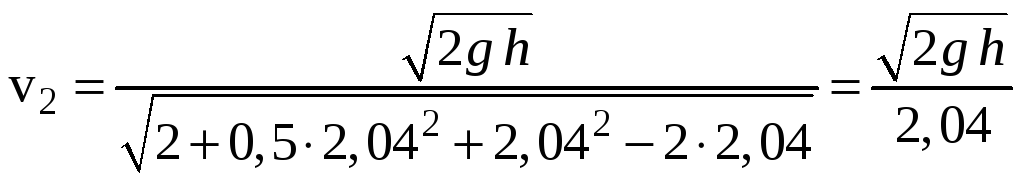Так как и , находим ;

откуда .

Коэффициент расхода: .

Коэффициент потерь: .

При входе в составной насадок струя сужается и минимальное по площади поперечное сечение струя имеет в сечении С-С, следовательно, в этом сечении скорость будет максимальной, а давление минимальным.

С-С—2-2

;

, где

- потери от сечения С-С до выхода – сечения 2-2; - потери на расширение от площади в сечении С до площади на выходе из первого насадка; - потери на расширение во втором насадке.

Используя теорему Борда-Карно, получим:

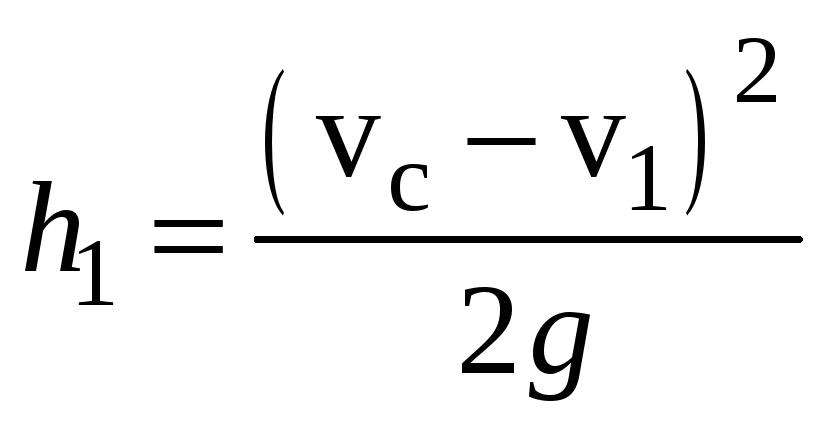и .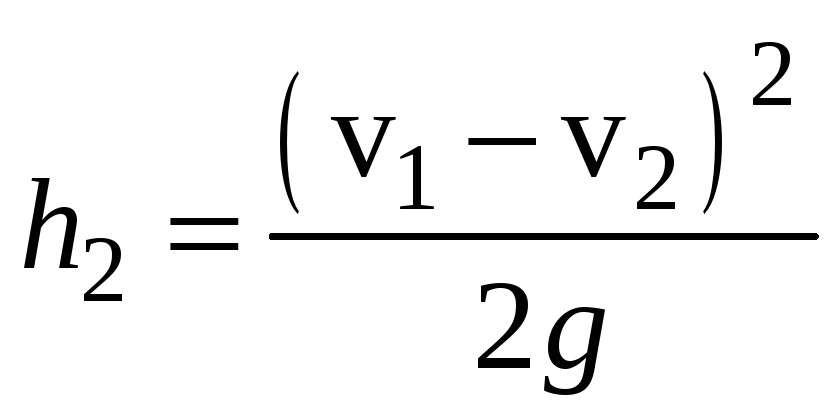

Обозначим , тогда:

;

.

Скорость в узком сечении определим из уравнения расхода: , учитывая, что , получаем:

После подстановки имеем:

;

.

Скорость на выходе может быть выражена как:

.

Тогда

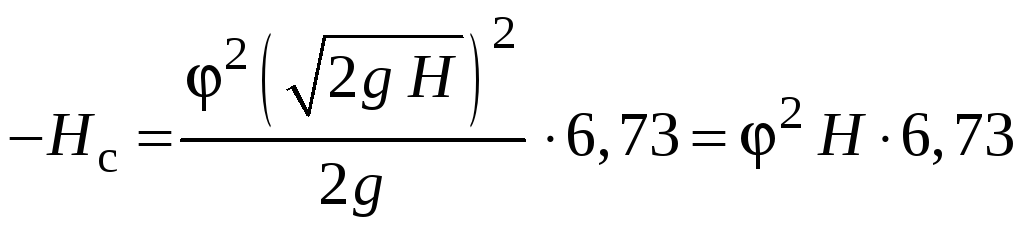, откуда .

При напор в баке достигнет максимального значения :

.

Ответ: ; .

З

адача 10.6

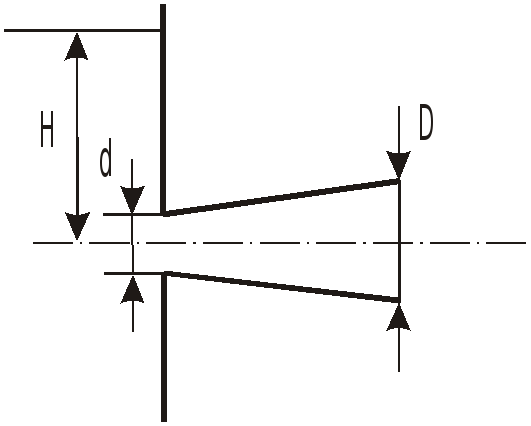
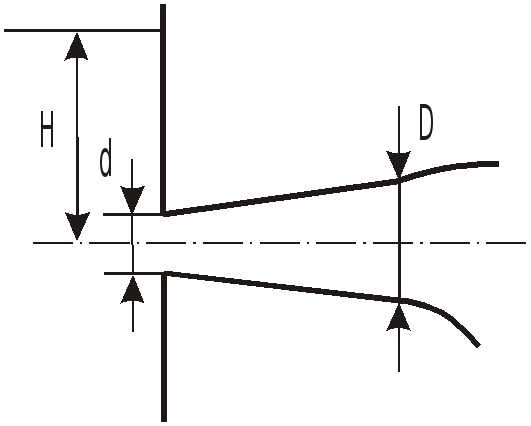
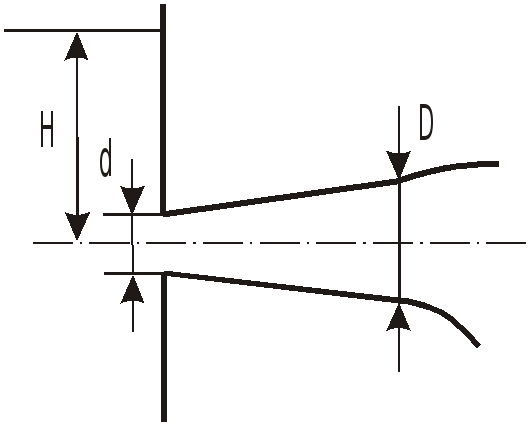
Подсчитать коэффициент расхода , отнесенный к площади узкого сечения, т.е.

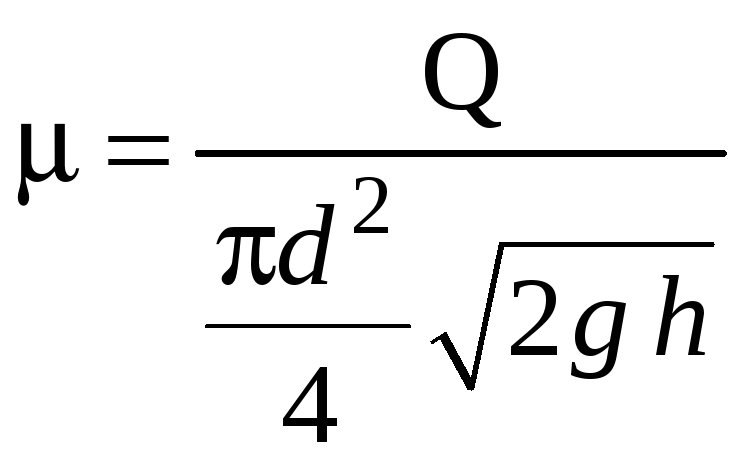, если коэффициент, отнесенный к выходному сечению известен.

Размеры .

Решение:

Расход через насадок , откуда

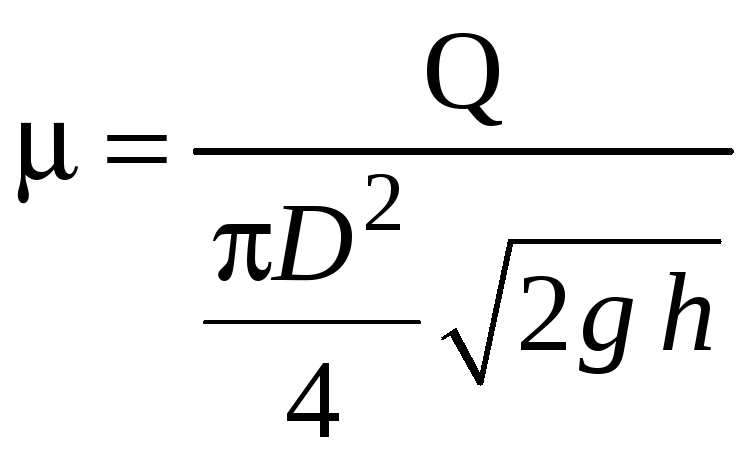
Коэффициент расхода, отнесенный к площади узкого сечения

;

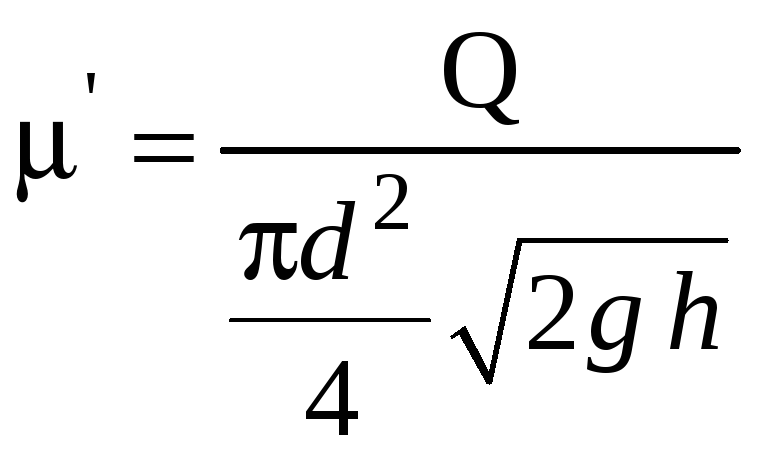Отношение .

.

Ответ:

З

адача 10.7

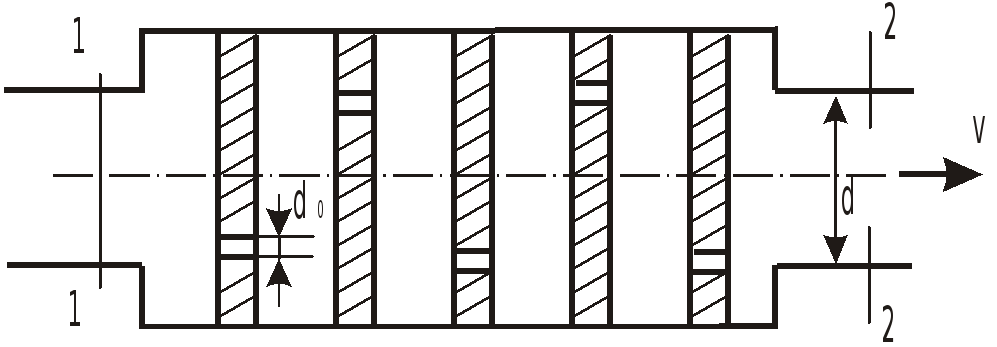
Определить коэффициент сопротивления пятиступенчатого дросселя, отнесенный к скорости в трубе с . Каждая ступень представляет сверление в толстой стенке . Скорость в промежутках гасится до нуля.

Решение.

Запишем уравнение Бернулли для сечений 1-1—2-2, учитывая, что ; (считаем режим течения турбулентным):

;

.

Потери в дросселе складываются из потерь:

• на расширение при входе ;

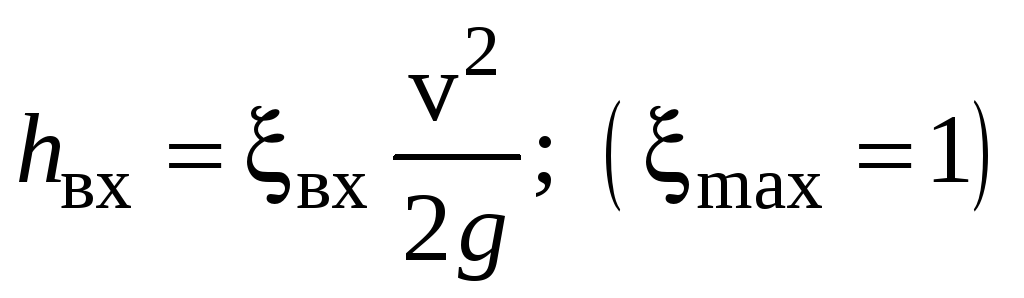• на сужение при выходе ;

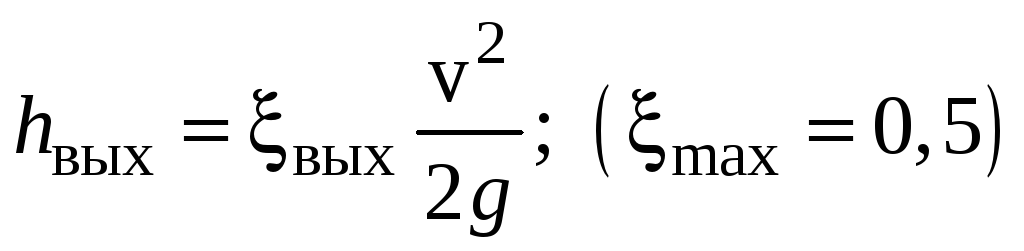• потерь на 5 ступенях дросселя ;

, при этом

.

Каждую ступень, представляющую сверление в толстой стенке , можно рассматривать как насадок. К потерям в насадке надо добавить потери на выходе из насадка, т.к. в промежутках между ступенями скорость гасится до нуля.

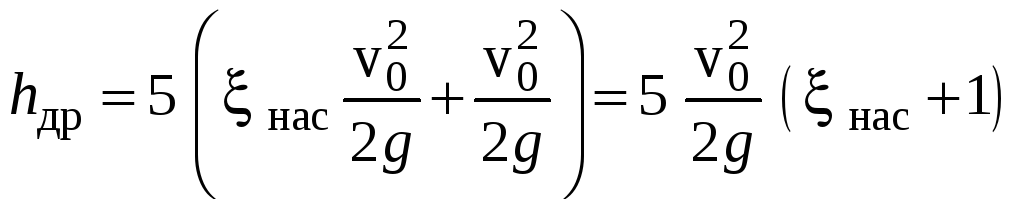
Из уравнения расхода выразим ;

.

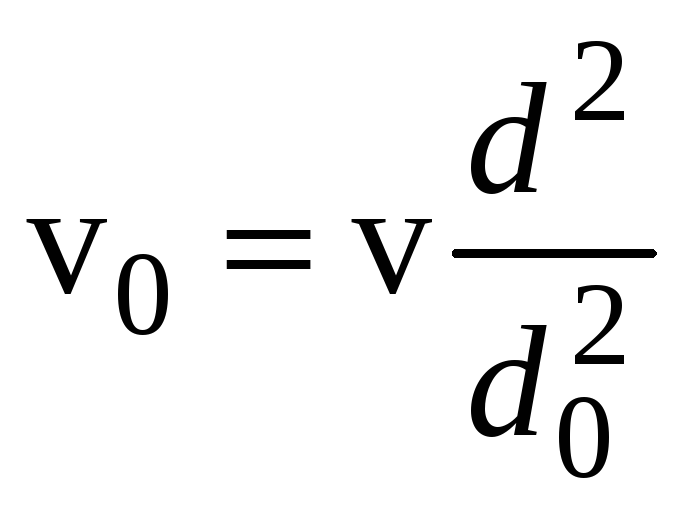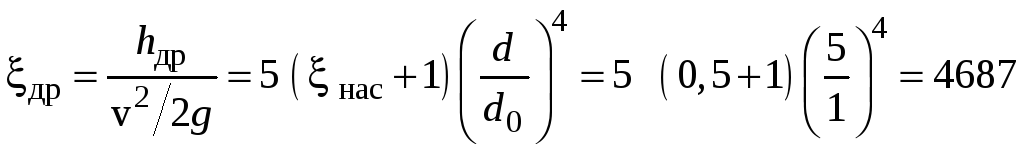Ответ: .

З

адача 10.8

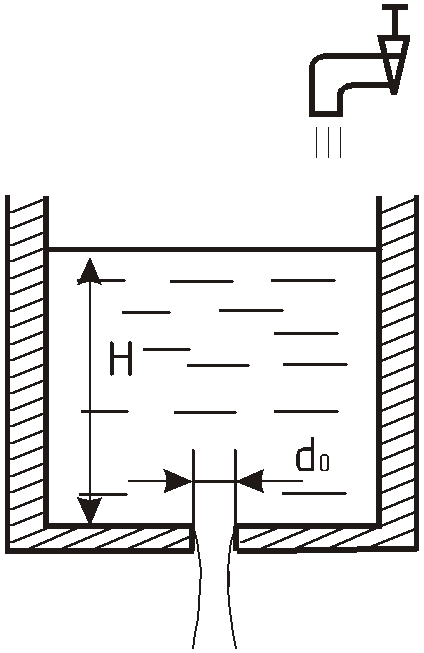
Вода вытекает из крана в бак с расходом .

В днище имеется отверстие с диаметром , через которое вода вытекает.

До какого уровня заполнится бак?

Ответ:

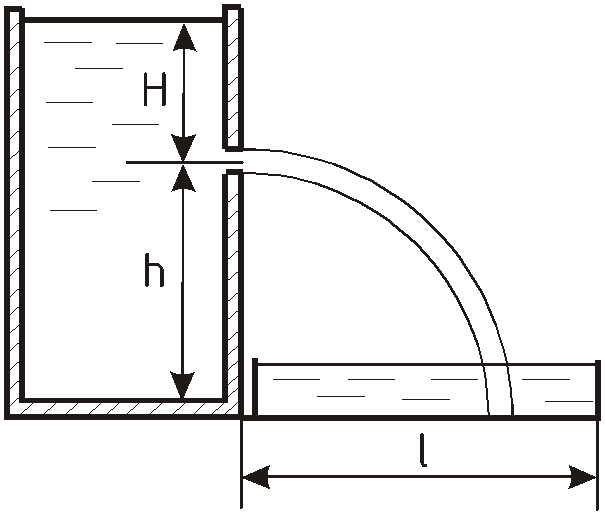
Задача 10.9

Ж

идкость вытекает из отверстия в тонкой стенке диаметром .

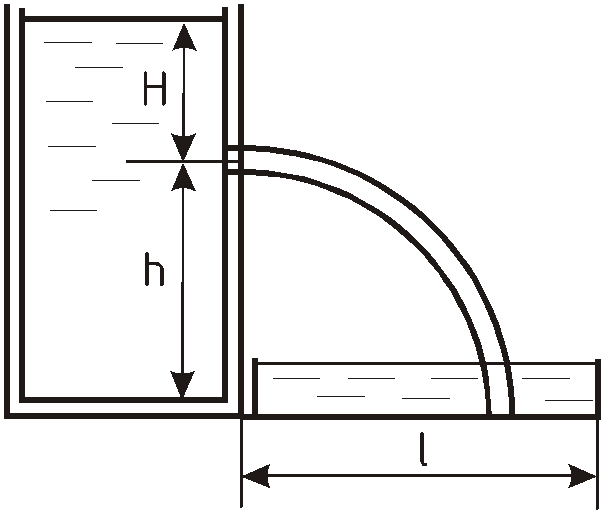
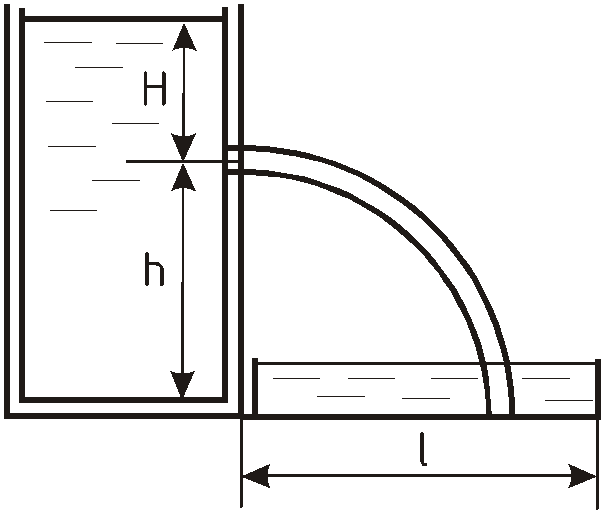
Определить значение максимально допустимого напора в баке , при котором струя не будет попадать за пределы водосборника и значение максимального расхода , если .

Ответ: .

З

адача 10.10

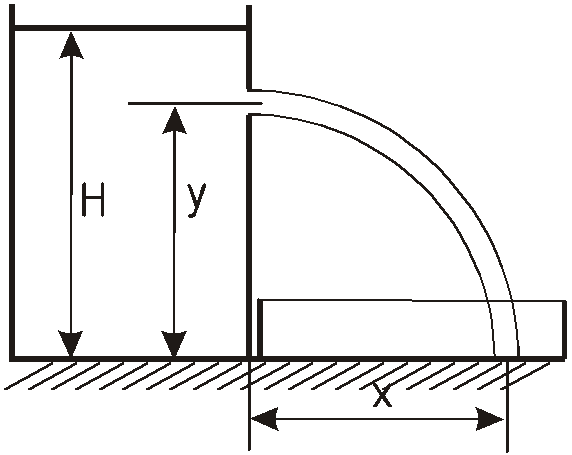
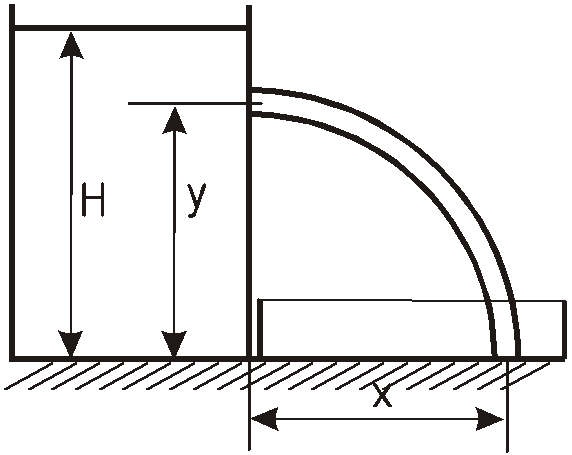
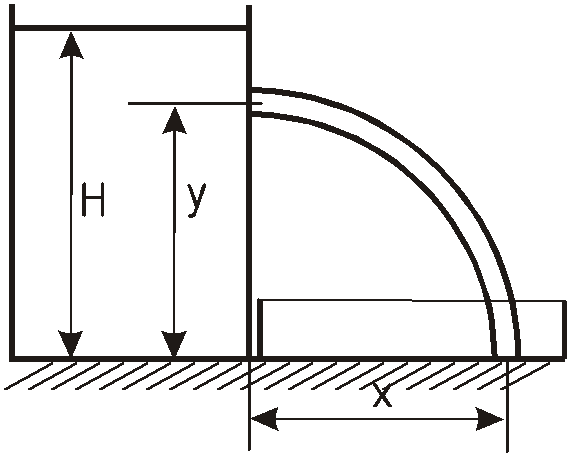
Из резервуара, установленного на полу и заполненного жидкостью до высоты , происходит истечение жидкости через отверстие в стенке.

На какой высоте должно быть расположено отверстие, чтобы расстояние до места падения на пол было максимальным? (Жидкость считать идеальной).

О

твет: .

Задача 10.11

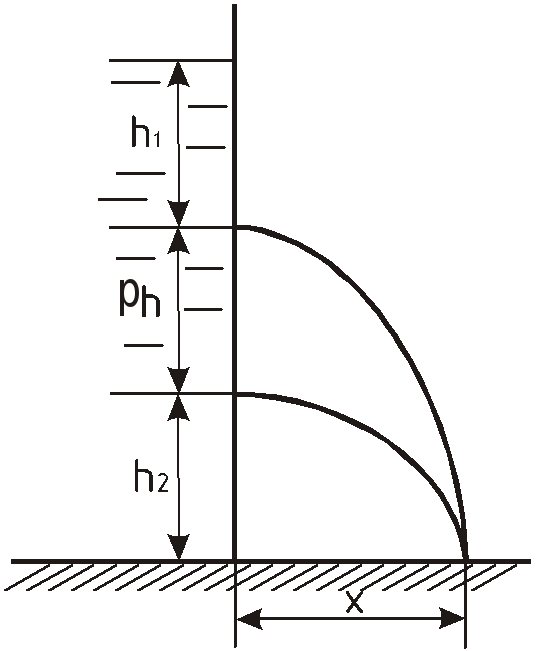
Жидкость вытекает из двух отверстий в тонкой стенке.

Каким должно быть расстояние между отверстиями , чтобы струи попадали в одну и ту же точку на полу?

Ответ: .

Задача 10.12

Как изменится расход жидкости, если к отверстию в тонкой стенке приставить:

1. Внешний цилиндрический насадок

2. Внутренний цилиндрический насадок

3. Конический расширяющийся насадок с .

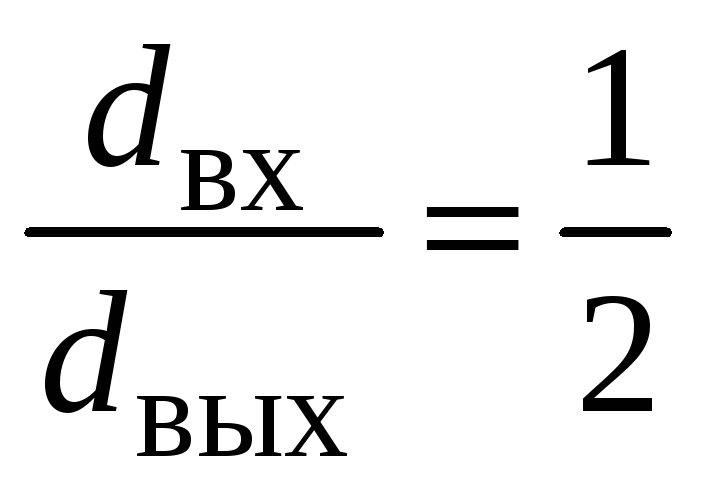Ответ:

1. Увеличится в 1,32 раза.

2. Увеличится в 1,14 раза.

3. Увеличится в 4 раза.

З

адача 10.13

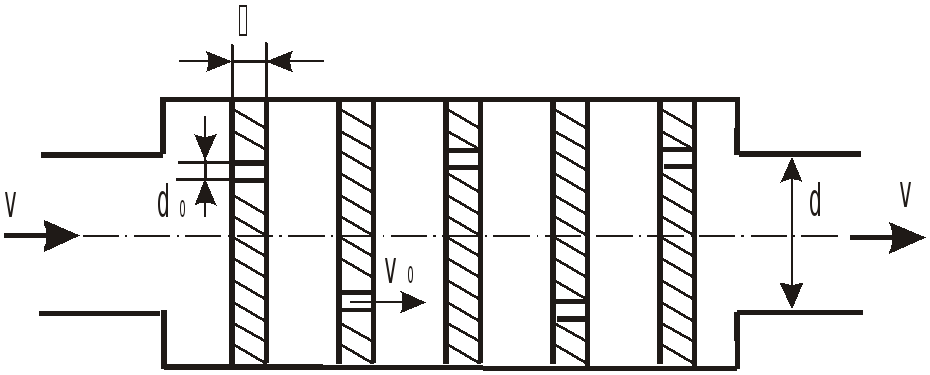
Определить коэффициент сопротивления многоступенчатого дросселя, отнесенный к скорости в трубке диаметром , если дроссель состоит из пяти ступеней. Каждая ступень представляет собой отверстие диаметром в стенке толщиной . Скорость в промежутках гасится до нуля.

Определить полную потерю давления в дросселе при скорости течения в трубке , если плотность жидкости .

Ответ: .

Задача 10.14

П

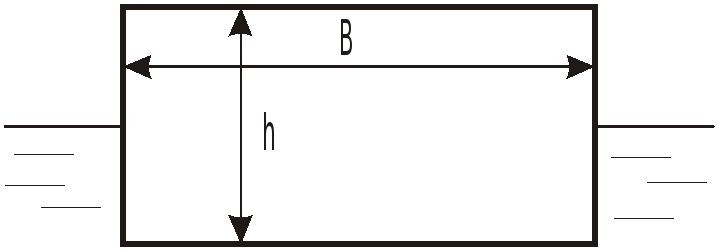
онтон, имеющий форму полого прямоугольного параллелепипеда, получил круглую пробоину диаметром в стенке у дна.

Вода вытекает в пробоину и постепенно заполняет его.

Определить, через какое время после получения пробоины понтон затонет. Масса понтона . Давление воздуха внутри понтона вследствие негерметичности палубы при заполнении его водой остается равным атмосферному. Размеры понтона: .

Коэффициент расхода .

Ответ: .