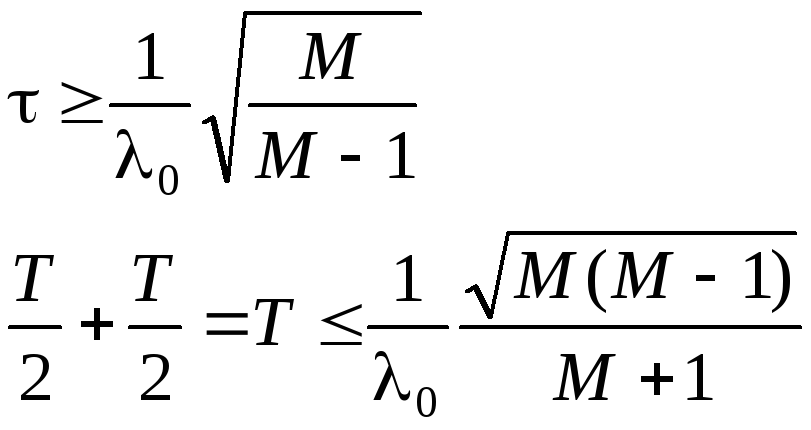1.1. Метод синтеза сар с цвм, обеспечивающий минимум времени протекания переходных процессов

Пусть тем или иным путем найдена желаемая дискретная передаточная функция разомкнутой системы

(3.7)

где (z) – желаемая передаточная функция замкнутой системы; - передаточная функция исходной нескорректированной системы.

Тогда искомая передаточная функция ЦВМ или дискретного фильтра имеет вид

(3.8)

Формирование желаемой функции (z) должно производится с учетом ограничений:

- необходимо, чтобы (z) содержала в качестве своих нулей все те нули передаточной функции W^*(z), модуль которой больше или равен единице;

- необходимо, чтобы выражение 1-(z) содержало в качестве своих нулей все те полюсы W^*(z), модуль которых больше или равен единице.

Невыполнение этих условий вызывает нарушение требований к грубости системы и вызывает ее неустойчивость, т.к. приводит к неустойчивым линейным программам ЦВМ, которые реализуют полученную передаточную функцию D(z).

Кроме того, получающаяся дробно-рациональная передаточная функция D(z) не должна иметь степень числителя выше, чем степень знаменателя, т.к. это приводит к необходимости знания будущего значения входного сигнала, что не может быть реализовано.

Таким образом, для решения задачи синтеза САР с цифровой коррекцией необходимо знать желаемую передаточную функцию замкнутой системы.

Если к системе предъявляются требования конечной длительностью переходного процесса необходимо, чтобы знаменатель передаточной функции замкнутой системы (характеристический полином) должен иметь вид z^l.

Например, для передаточной части системы с ЦВМ , при k = 1 с^-2, T = 1 c, желаемую передаточную функцию замкнутой системы можно взять в виде

.-

Переходный процесс при g(t) = 1(t) в этом случае закончится за два периода дискретности. Так как

,

то после деления числителя на знаменатель

.

Учитывая формулу z-преобразования

,

получим следующие значения функции x[n] на выходе системы в дискретные моменты времени: при t=0, x[0]=0; при t=T, x[1]=1/2; при t=2T, x[2]=1; при t=3T, x[3]=1 и т.д. при всех значениях x(t)=nT.

Дискретная передаточная функция ЦВМ, реализующая такой переходной процесс, определяется выражением (3.8). Определив по (3.1) и подставив в (3.8), получим формулу, определяющую алгоритм работы ЦВМ.

1. 2. Метод расчета дискретного ку, обеспечивающий заданный запас устойчивости

Расчет дискретных корректирующих средств можно проводить, используя дискретные частотные передаточные функции. Тогда

,

где - желаемая и исходная передаточные функции; - частотная передаточная функция дискретного корректирующего устройства.

Для получения частотной передаточной функции необходимо в выражении для передаточной функции сделать подстановку в z = e^jT.

Частотные характеристики в этом случае оказываются периодическими функциями частоты ω с периодом 2/T.

Более удобным для получения частотных характеристик является использование псевдочастоты. Обычно для этой цели применяют так называемое w–преобразование при помощи которого окружность единичного радиуса e^jT отображается на мнимую ось плоскости комплексной величины w.

Для преобразования используется подстановка или соответственно .

Подставляя в последнее выражение z= e^jT, получим

,

где представляет собой относительную псевдочастоту.

Однако, наиболее часто на практике используется так называемая абсолютная псевдочастота

При малых частотах (<2/T) абсолютная псевдочастота практически совпадает с обычной . Это является весьма удобным, т.к. при выполнении условия T<2 частотные характеристики, построенные в функции псевдочастоты, практически совпадают с характеристиками, построенными в функции обычной круговой частоты.

Передаточная функция с w–преобразованием получается в соответствии со следующим выражением:

.

Для получения частотной передаточной функции необходимо сделать подстановку w=j

.

Построение логарифмических частотных характеристик производится в функции псевдочастоты раздельно для области низких частот (T<2) и для области высоких частот T>2. В области низких частот построение ЛАЧХ и ЛФЧХ сводится, по сути дела, к построению логарифмических характеристик исходной непрерывной части.

.

В связи с этим на цифровые системы можно распространить правила построения запретной области для ЛАЧХ, используемые для линейных систем с целью обеспечения заданной точности.

Построение средне- и высокочастотной частей желаемой ЛАЧХ, обеспечивающей заданный запас устойчивости, производится с учетом некоторых особенностей. Они сводятся к методике учета малых постоянных времени и к учету эффекта транспонирования частот в колебательных и консервативных звеньях. Для обеспечения построения ЛАХ в этих областях можно воспользоваться таблицами, приводимыми в литературе по теории управления [1, 3].

Таким образом, построив ЛАЧХ желаемой L_ж() и исходной L() систем, можно получить ЛАЧХ последовательного корректирующего устройства как

.

После определения D(j) подстановкой j=2/T можно получить передаточную функцию , а затем переходя от w- к z-преобразованию - передаточную функцию .

Пример. Пусть передаточная функция непрерывной части САР

.

Тогда

а

.

Соответствующая ЛАЧХ L() построена на рис.3.3.

0

L, L_ж

1/τ 2/T

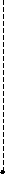
-40 дБ/дек

_ср



₀

-20 дБ/дек

L_ж()

-20 L()

Рис. 3.3 Выбор желаемой ЛАЧХ

Примем желаемую ЛАЧХ в виде, изображенном на рис. 3.3. Ей соответствует

.

Передаточная функция корректирующего устройства в этом случае имеет вид

.

Переход к передаточной функции ЦВМ дает

,

которой соответствует устойчивая программа работы ЦВМ. Параметры характеристик определяются, как и для непрерывных систем, через базовую частоту и показатель колебательности M.