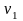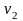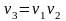37. Применение дискретных моделей при идентификации непрерывного ОУ, дискретная модель непрерывного объекта, выбор периода дискретизации.

Постановка задачи та же самая, что и в методе выше:

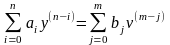(1) где

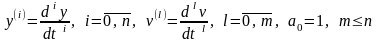
Задача заключается в нахождении n+m+1 коэффициентов 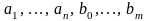по результатам измерени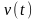й и 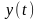в дискретные моменты времени .

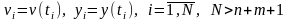1. Так как измерение в виде массива, необходимо составить дискретную модель ОУ. В качестве метода составления дискретной модели используют следующее (соотношение между z и p переменными)

Составление дискретной модели ОУ: (используется первый член степенного ряда ln)

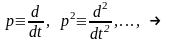
z будем представлять в виде оператора сдвига на один период в сторону опережения, т.е. 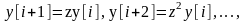(2)

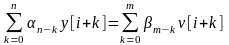ДУ(1) приводится к разностному уравнению (3): (3)

Это уравнение является дискретной моделью непрерывного объекта, а коэффициенты 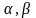– функциями коэффициентов ДУ(1)

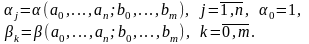(4)

2. Введём в рассмотрение дискретные операторные ПФ:

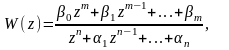и выход объекта запишем через передаточную функцию 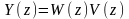.Оценку выхода объекта вычислим так же как и выход объекта, за исключением того, что коэффициенты ПФ объекта заменяются оценками: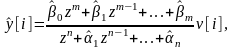 (5)

Оценки вводятся так как точное определение коэффициентов ПФ невозможно, так как вход и выход объекта искажены помехами.

Вводим ошибку идентификации: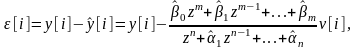 (6)

На основании ошибки формируется квадратичный критерий идентификации, который является функцией оценок коэффициентов:

,

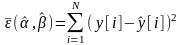Приводим (6) к общему знаменателю и получаем:

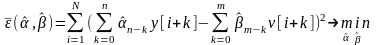
Приходим к оптимизации задачи, решение которой находим оценки коэффициентов , и решая систему из (n+m+1) уравнений оценки коэффициентов ДУ 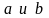. Выбор периода дискретизации

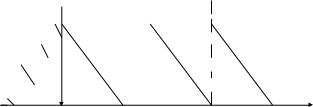
При дискретизации меняется спектр сигнала, который подвержен квантованию.

0

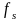
При дискретизации с частотой спектр клонируется. – верхняя частота.

Если частота выбирается неправильно, происходит наложение спектров и искажение сигнала. Повторение спектра на частотах 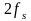_, и т.д.

0

Дискретизация по времени приводит к появлению периодических копий спектра сигнала, которые накладываются друг на друга (эффект наложения спектров или элайзинг). При слишком малой частоте дискретизации эти копии перекрываются, что приводит к искажениям сигналам при его восстановлении.

Гармоники сигналов с частотами выше частоты дискретизации отображаются в частоты ниже этой частоты, создавая помехи. Предельная частота дискретизации , при которой перекрытие ещё не происходит, равна удвоенной верхней частоте спектра сигнала 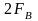. Эта частота называется частота Найквиста.

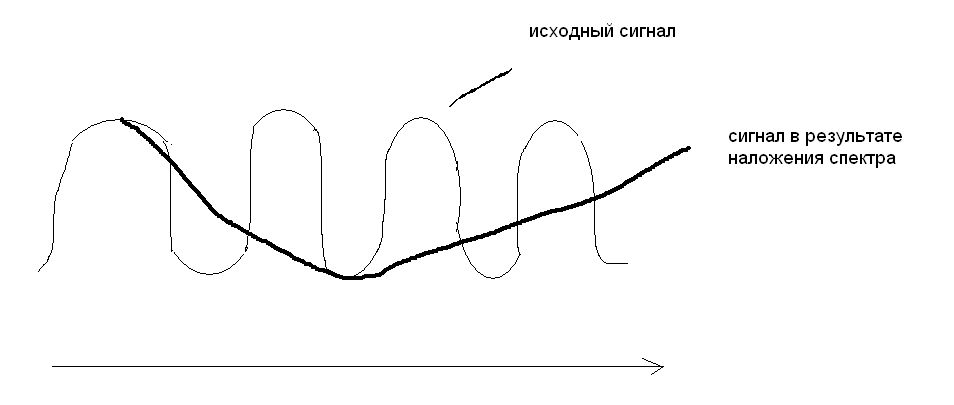
Обозначим – частота дискретизации сигнала, T – период дискретизации.

Критерий Найквиста

Сигнал, подлежащий дискретизации, имеет ширину спектра .

Частота дискретизации сигнала с шириной полос 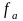должна удовлетворять условию 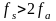, в противном случае информация о сигнале будет искажена.

Эффект наложения спектров возникает, когда .

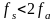Теорема Кательникова

Если непрерывный сигнал имеет спектр, ограниченный частотой , то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени

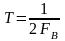, то есть с частотой .

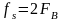38. Дробные факторные планы (дробный факторный эксперимент): дробные реплики, определение, правило построения дробных факторных планов, генератор плана.

Дробным факторным экспериментом (ДФЭ) называется некоторая часть полного факторного эксперимента, выбранная по определенному правилу. ПФЭ 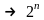(если планируется полный факторный эксперимент, то число опытов ). Например, при n = 5 на проверку адекватности линейной модели остается 26 степеней 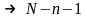При этом из множества точек факторных планов 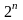может быть отобрана некоторая часть, представляющая дробный факторный план (ДФЭ) План, включающий только половину экспериментов ПФЭ, называется полурепликой, включающий четвертую часть опытов – четверть репликой и т. д. Краткое обозначение указанных дробных реплик – 2^n-1, 2^n–2.

Правило построения дробных факторных планов

ДФП типа : 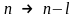основных факторов ПФЭ

ДФП типа строится след. образом. Из n факторов выбирают основных факторов. На них строится ПФЭ с матрицей 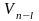. Этот план затем дополняют столбцами, соответствующими оставшимся факторам. Эти столбцов формируются на основании алгоритмов, которые называют генераторами плана.

Генератор плана представляет собой произведение основных факторов, определяющее значение элементов каждого из дополнитель­ных столбцов матрицы плана. Для формирования каждого из столбцов используют свой генератор плана. Это произведение включает в себя от 2 до факторов. Для построения требуется генераторов.

Построение дробного факторного плана для п = 3 - исходные факторы

- основные факторы. Построим ДФП в виде полуреплики . Из исходных факторов выделим 2 основных и на этих основных факторах построим полный факторный план . Этот план включает в себя 4 эксперимента и 2 фактора.

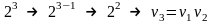
-1	+1	-1
+1	+1	+1
-1	-1	+1
+1	-1	-1

Чтобы сгенерировать значение 3-го столбца, используют генератор плана. Единственное произведение -- генератор плана.

ДФЭ - 2^3-1 = 4 ПФЭ - 2³ = 8

39. Оценка параметров нелинейного статического оу..

ОУ представляет собой нелинейное безынерционное звено с одним входом и одним выходом. Его статическая характеристика описывается нелинейной функцией m-параметров: y=f(c₀ c₁ … c_m). f является дифференцируемой по параметрам (c₀ c₁ … c_m) функцией.

Требуется оценить значения параметров (c₀ c₁ … c_m), которые полностью определяют статическую характеристику объекта. Другими словами, их надо оценить по результатам наблюдений за входами и выходами объекта.

На вход данного нелинейного объекта подается сигнал v который измеряется в дискретные моменты времени. В эти же моменты измеряется выход объекта как реакция на входной сигнал. N-число измерений.

v_i->y_i=f_i(c₀ c₁ … c_m)+e_i, i=1,N (1). Известную функцию f с неизвестными параметрами можно представить как модель нелинейного безынерционного объекта. Тогда результаты измерений связаны с измерениями выхода модели соотношением (1). Где e_i случайная составляющая, которая характеризуется корреляционной матрицей Re, размерности NxN: Re=(Ri,j); i,j=1,N. (Ri,j)-коэффициенты корелляционной матрицы, называемые коэф. между i и j измерениями случ. составляющей. В качестве критерия идентификации выберем квадратичный критерий вида: 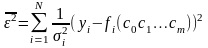(2) Поскольку f нелин. ф-ция, то аналитически решить поставленную задачу достаточно сложно. Пусть известна грубая оценка вектора коеф. нелинейной зависимости: 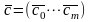. Тогда значение в i-том измерении, зависящ. от неизв. векторных оценок можно представить как ф-цию, зависящ. от грубых оценок и некоторой поправки (Δс).

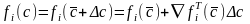(*) Разложим ф-цию f_i в окрестности грубой оценки в ряд Тейлора и ограничимся 2мя первыми членами, т.е. осуществим лин. аппроксимацию. 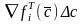- скалярное произведение градиента функции на вектор поправок 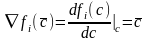(2а) С учетом (*) выход объекта можно записать в виде соотношения (3), которое связывает выход объекта с его моделью: 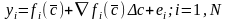(3), (4), где .

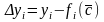(4) представляет собой линейную модель наблюдения. По результатам наблюдения за выходом и входом нужно оценить поправку Δс на основании линейной модели наблюдения (4).

Вводится вектор отклонения выхода Δy=(Δy₁ Δy₂ … Δy_N), матрица наблюдений Н, строками которой являются градиенты нелинейной функции f:

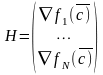; Δy=HΔc+е (5); е=(e₁ e₂ …e_N).

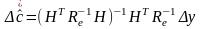
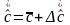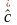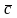Используя МНК получаем оценку поправки: , где -оценка перв. приближения. -грубая оценка