40*. Интегрирование дифференциальных уравнений с разделяющимися переменными и уравнений, приводящихся к ним. Общий интеграл.

Дифференциальное уравнение вида φ(y)dy=f(x)dx, где коэффициент при dx зависит только от х, а коэффициент при dy -только от y, называется уравнением с раздельными коэффициентами. Общим интегралом такого уравнение в расчете, что f(x) и φ(y) непрерывны, будет

Уравнения вида φ₁(y)dyf₁(x)dx= φ₂(y)dyf₂(x)dx=0, в которых коэффициенты при дифференциалах распадаются на множители, зависящие только от x и y, называются ур-ями с разделяющимися переменными.

Вынесем за скобку φ₁(y)f₂(x).

Если φ₁(y)f₂(x)≠0, то путем деления на это произведение ур-е приводится к ур-ю с разделенными переменами:

=0

Почленное интегрирование =С определяет в неявной форме общее реш-е исходного ур-я.

Общий интеграл- общее решение ДУ, выраженное в неявной форме.

Если φ₁(y)f₂(x)=0, те φ₁(y)=0, f₂(x)=0. Если они имеют вещественные решения y=ρ, x=ε,то последние могут оказаться особыми решениями(особое решение- решение дифференциального ур-я, которое не может быть получено из общего решения ни при одном частном значении произвольной постоянной, включая ±∞). Других особых решений у ур-я быть не может.

ДУ вида , где abc- постоянные, заменой переменных z= ax+by+c преобразуется в ур-е с разделяющимися переменными.

y=, и подставляя в ур-е, получаем

Разделяя переменные и интегрируя, находим .

41. Методы интегрирования линейного дифференциального уравнения первого порядка ( с примерами). Уравнение Бернулли.

ЛДУ 1ого порядка- ур-е вида y'+p(x)y=f(x), где p(x), f(x)- непрерывные ф-ии на интервале a<x<b.

1 Способ) метод вариации постоянной.

a)OO: y'+p(x)y=0

dy/dx+p(x)y=0- ур-е с раздел.переменными

ln|y|=-ln|c|

y=С, где С- произвольная постоянная≠0.

Может быть потеряно реш-е y=0. Тк его можно получить при С=0 заключаем, что y=С-общее решение ЛОУ.

б)реш-е ЛНО- метод вариации произвольной постоянной С.

Ф-я С(x)- такова, что при подстановке y=С(x) и y'= С’(x) С(x) в исходное выражение, оно обращалось в тождество на интервале a<x<b, те

С’(x)f(x)

C(x)=+C, где С- произвольная постоянная.

Подставляя вместо С(x) полученное выражение, находим общее решение ЛУ на интервале { a<x<b, -∞<y<+∞}:

y=( +C)

Yон=Yоо+Yчн

2Способ) ур-е Бернулли

y= u(x)v(x) (u,v- неизвестные ф-ии). Исходное ур-е преобразуется к виду u'v+uv'+p(x)uv=f(x).

Одна из ф-й может быть выбрана совершенно произвольно, лишь бы произведение uv=y. Так, например v= любое частное решение ур-я v'+p(x)v=o.

Например, v=, обращающее u в 0.

Тогда u'=f(x)/v=f(x)

u= +C

Общее решение исходного ур-я=y= uv=(C+.

42. Линейные дифференциальные уравнения n-го порядка. Структура общего решения линейного однородного дифееренциального уравнения. Фср. Определитель Вронского и его свойства.

ЛДУ n-ого порядка- ур-е, линейное относительно неизвестной ф-ии и ее производных и имеет вид

a₀(x)y⁽ⁿ⁾+a₁(x)y^(n-1)+…+a_n-1(x)y’+a_n(x)y=φ(x)|: a₀(x)

φ(x)=0- ЛОУ

φ(x)≠0- ЛНОУ

y⁽ⁿ⁾+p₁(x)y^(n-1)+…+p_n-1(x)y’+p_n(x)y=g(x)- (1)ур-е в приведенном виде

Для ЛОУ:

*если y₁- решение ЛОУ, то С y_1, где С- произвольная постоянная также является решением этого ур-я.

*Сумма y₁+ y₂ решений ЛОУ является решением того же ур-я.

1⁰Линейная комбинация с произвольными постоянными реш-й y₁, y₂,…, y_m ЛОУ является реш-ем того же ур-я.

*если ЛОУ (1) с действительными коэффициентами p_i(x)∈R имеет комплексное решение y(x)=u(x)+iv(x),то действительная часть этого решения Rey=u(x) и его мнимая часть Imy=v(x) в отдельности являются решениями одного и того же ур-я.

Ф-ии y₁(x), y₂(x),…, y_n(x) называются линейно зависимыми на некотором интервале (a,b), если существуют постоянные величины a1,a2,…,an≠0 такие, что для всех x интервала (a,b) справедливо тождество a₁ y₁(x)+a₂ y₂(x)+…+a_n-1(x)y’+a_n y_n(x)=0. Если ф-ии линейно завис.,то хотя бы одна из них является линейной комбинацией остальных.

Если же тождество справедливо лишь при a1=a2=…=an=0, то ф-ии y₁(x), y₂(x),…, y_n(x) называются линейно независимыми на интервале (a,b).

*если ф-ии y₁(x), y₂(x),…, y_n(x) линейно зависимы на интервале (a,b), то определитель(о. Вронского)

W(x)=W[y₁, y₂,…, y_n]==0 на этом интервале.

Условие линейной независимости частных решений:

* если линейно независимые ф-ии y₁(x), y₂(x),…, y_n(x) являются решениями ЛОУ (1) с непрерывными на интервале (a,b) коэффициентами p_i(x), то составленный для них определитель Вронского ни в одной точке интервала (a,b) не= 0.

Общим решением ЛОУ (1) с непрерывными на (a,b) коэффициентами p_i(x) (i=1,2,…,n) является линейная комбинация y_оо= n линейно независимых на том же интервале частных решений y_i с произвольными постоянными коэффициентами.

1⁰максимальное число линейно независимых решений ЛОУ равно его порядку.

ФСР- любые n независимых частных реш-й ЛОУ n-ого порядка.

*y_oн=y_oo+y_чн

43. Структура общего решения линейного неоднородного дифференциального уравнения. Метод вариации произвольных постоянных для отыскания частного решения линейного неоднородного дифференциального уравнения n-го порядка.

ЛНДУ решаются методом вариации произвольных постоянных. Сначала находится общее решение однородного уравнения , имеющего ту же левую часть, что и исходное неоднородное уравнение . Затем решение уравнения находится в виде , т.е. предполагается, что постоянные С явл ф-ми независимой переменной х. При этом ф-и С₁(х) и С₂(х) могут быть получены как решение системы

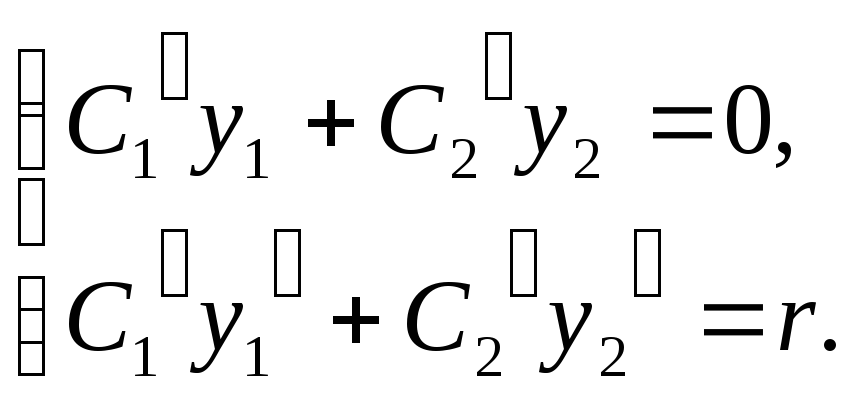
У_он=у_оо+у_чн

максимальное число решений уравнения равно его порядку.

общее решение

44*. Линейное однородное дифференциальное уравнение с постоянными коэффициентами. Характеристический многочлен и характеристическое уравнение. Построение фундаментальной системы решений в случае простых корней характеристического многочлена (действительных и комплексных).

Уравнение вида y'+p(x)y=f(x), где p(x), f(x)- непрерывные ф-ии на интервале a<x<b называется ЛДУ 1ого порядка.

Если f(x)= 0, то уравнение называется однородным.

Если в ЛО ур-ии y⁽ⁿ⁾+p₁(x)y^(n-1)+…+p_n-1(x)y’+p_n(x)y=0

Все коэффициенты pi постоянны, то его частные решения могут быть найдены в виде y=e^kx, где k- постоянная. Подставляя в ур-е

(kⁿ+p₁k^n-1+….+p_n-1 k+ p_n) e^kx=0

Сокращая на e^kx получаем так наз. Характеристическое ур-е

kⁿ+p₁k^n-1+….+p_n-1 k+ p_n =0

Это ур-е n-ой cтепени определяет те значения k, При которых y= e^kx является решение исходного ДУ с постоянными коэф-ами.

1.k₁, k₂,…,k_n –вещественные и различные

ФСР: e^k1x, e^k2x,…, e^knx

2. k₁= k₂=…=k_m=k^~,

k^~- m -кратный корень ур-я, а все остальные n- m корней различные

ФСР: e ^{k~ x},x e ^{k~ x},…, x^m-1 e ^{k~ x}, e ^{km+1 x}, e ^{kn x}

3. k₁=α+iβ, k₂= α-iβ, k₃=γ+iδ, k₄= γ-iδ, остальные корни вещественные

ФСР: e^αxcosβx, e^αxsinβx, e^γxcosδx, e^γxsinδx, e^k5x,…, e^knx

4. Если k₁=α+iβ- m-кратный корень характерестического ур-я (m≤n/2), то k₂= α-iβ также будет m-кратным корнем

ФСР: e^αxcosβx, e^αxsinβx, xe^αxcosβx, xe^αxsinβx,x^m-1 e^αxcosβx, x^m-1 e^αxsinβx,…, e^k2m+1x,…, e^knx