33. Свойства определенных интегралов с примерами.

1. Условия существования определенного интеграла.

Если ф-я F(x) интегр. на [a,b], то она ограничена на том отрезке. Условие ограниченоостти необходимое, но недостаточное.

2.Классы интегрируемых ф-й:

1)если ф-я непрерывна на отрезке [a,b],то она интегрируема.

2) если огран. ф-я на [a,b] имеет лишь конечное число точек разрыва, то она интегрируема.

3)монотонная ограниченная ф-я всегда интегрируема.

Cв-ва:

1)если ф-я интегр. на [a,b], то она интегр. на [b,a].

, =0

2)если ф-я интегр. в наибольшем из [a,b] , [a,c] и [с,b], тогда

+

3) если ф-я интегр. на [a,b], то kf(x), где k=const, также интегр. на [a,b].

4) если обе ф-ии f(x) и g(x) интегр. на [a,b], то их алгебраическая сумм также ) интегр. на [a,b].

5) если ф-я интегр. на [a,b], f(x)≥0, a<b, то ≥0

6) если обе ф-ии f(x) и g(x) интегр. на [a,b], f(x) ≤ g(x) (f(x) <g(x)),

то ()

a<b

7) если ф-я интегр. на [a,b], a<b

≤

8) если ф-я интегр. на [a,b], a<b и на всем этом промежутке справедливо нер-во

m≤f(x)≤M, то m(b-a)≤ ≤M(b-a) (m≤ ≤M)

Теорема о среднем:

если ф-я f(x) непрерывна на [a,b], то на этом отрезке сущ. (∙) С такая,что =f(c)(b-a)

Величина опр.интеграла= Sприложения с высотой f(c) и основанием (b-a).

34*. Определенный интеграл как функция верхнего предела. Основная формула интегрального исчисления (с примерами).

Пусть ф-я f(x) определена и неограниченна на отрезка [a,b] и a=x₀<x₁<…<x_n= b – произвольное разбиение отрезка на n промежутков. На этом отрезке [x_i-1,x_i] выбрана точка ε_i. Тогда сумма называется интегральной суммой f(x) на отрезке [a,b], а ее предел при max _1≤i≤n ∆x_i= max _1≤i≤n (x_i- x_i-1)→0, если он существует и конечен, называется определенным интегралом ф-ии от a до b.

Если ф-я f(x) интегрируема на [a,b], то она интегрируема на отрезке [a,x], где ∀x∈[a,b].

Ф(x)= – интеграл с переменным верхним пределом.

Cв-ва:

1. f(x) интегрируема на [a,b]→ Ф(x) непрерывна на этом отрезке

2. f(t) непрерывна в точке t=x→ в этой точке Ф(x) имеет производную= f(x)

Ф’(x)∃; Ф'(x) =f(x)

d/dx = f(x)

Производная интеграла непрерывной ф-ии по переменному верхнему lim существует и равна значению подинтегральной ф-ии в точке, равной верхнему lim. Всегда существует первообразная для непрерывной переменной ф-ии.

Пусть F(x)- другая первообразная для (x) интегрируема на [a,b].

Ф(x)= F(x)+C;

Пусть x=a → → C=-F(a)

Пусть a=b

– Формула Ньютона-Лейбница

35. Замена переменной и формула интегрирования по частям в определенном интеграле с демонстрацией на конкретных примерах.

Замена переменной при следующих условиях:

1)ф-я f(x) непрерывна на [a,b]

2)ф-я x=φ(t) непрерывна вместе со своей производной φ'(t) на отрезке [α,β]

3)a= φ(α), b= φ(β)

4)ф-я f(φ(t)) определена и непрерывна на отрезке [α,β], тогда

Если ф-ии u(x), v(x) –дифференцируемы на [a,b], то

36. Определение площадей и объемов тел вращения с помощью определенных интегралов (с примерами).

Криволинейная трапеция-плоская криволинейная фигура, ограниченная отрезком оси абцисс [a,b], кривой y=f(x), где f(x) непрерывна и неотрицательна на этом отрезке, и 2мя прямыми x=a,x=b. Если ф-я незнакопостоянна, то определнный интеграл численно равен алгоритму суммы S криволинейной трапеции, лежащей над и под осью ox. В эту сумму S крив. Трап., леж. Над осью входят со знаком +, а под ней- со знаком -.

П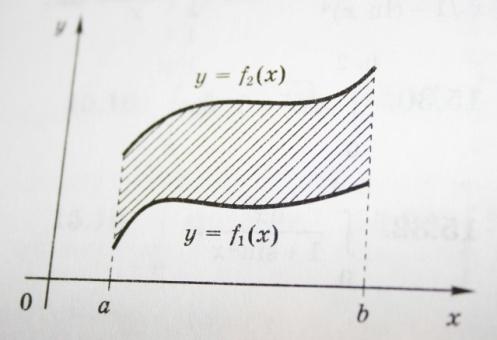лощадь S, ограниченная непрерывными кривыми y=f1(x), y=f2(x), вертикалями x=a, x=b, где f1(x)≤ f2(x) при a≤x≤:

S=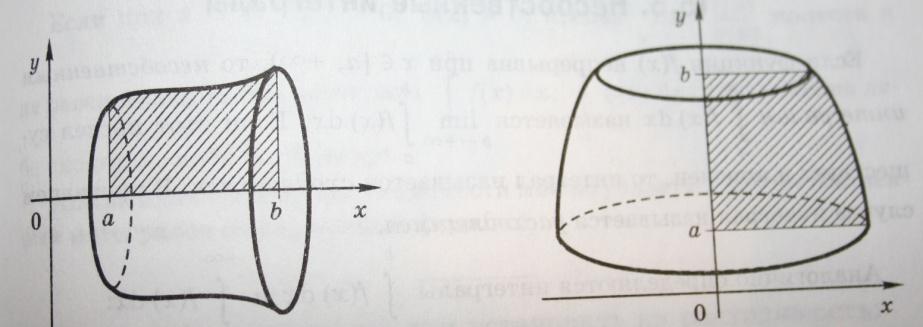

Объем тела, образованного вращением вокруг оси Ox криволинейной трапеции, ограниченной кривой y=f(x)≥0 и прямыми x=a, x=b (a<b), y=0:

=

Объем тела, образованного вращением вокруг оси Oy криволинейной трапеции, ограниченной кривой x=g(y)≥0 и прямыми y=a, y=b (a<b), x=0: V =