1.4 Angles complémentaires, supplémentaires, opposés par le sommet.
Mots à retenir
des angles complémentaires ( углы, дополняющие друг друга до прямого угла)
des angles supplémentaires (углы, дополняющие друг друга до развёрнутого угла)
des angles adjacents (углы, которые имеют общую вершину,общую сторону и лежат в разных полуплоскостях относительно их общей стороны )
des angles opposés par le sommet (вертикальные углы)
des droites sécantes (пересекающиеся прямые)
le point d’intersection (точка пересечения)
des droites parallèles (параллельные прямые)
des droites perpendiculaires (перпендикулярные прямые)
Remarque: deux angles adjacents supplémentaires sont « смежные углы ».
1) Deux angles sont complémentaires quand la somme de
leurs mesures est égale à la mesure d’un angle droit.
2)
Deux
angles sont supplémentaires
quand la
somme de
leurs mesures est égale à la mesure d’un angle plat.
3)
Deux angles sont adjacents
lorsque :
ils ont le
même sommet ;ils ont un côté commun ;ils sont
placés de part et d’autre de côté commun
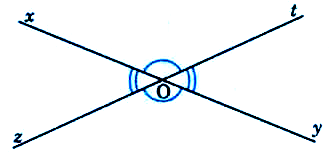
4) Deux angles opposés par le sommet : ont le même
sommet ; les côtés de l’un prolongent les côtés de
l’autre.
Remarques :
Deux angles opposés par le sommet sont
égaux. Deux droites (XY) et (ZT) sécantes en O définissent quatre
angles. Les angles
XOT
et
YOZ
sont opposés par le sommet. De même, les angles
XOZ
et
YOT
sont opposés par le sommet.
5) Des droites formant un angle droit sont dites
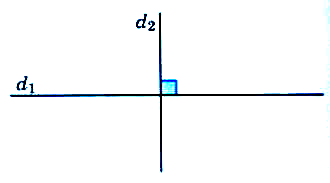perpendiculaires.
d1
d
6) Des droites parallèles sont des droites qui n’ont
aucun
point commun.
d1║d2
Exercices
51) Les angles de la figure 1 sont dit complémentaires, ceux de la figure 2 sont dit supplémentaires.
1) 2)
-
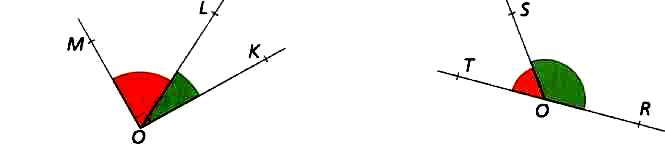
Expliquer les mots complémentaires et supplémentaires (noter qu’ils sont toujours au pluriel).
-
L’angle
KOL
de la figure 1 mesure 390.
Calculer l’angle
MOL. -
L’angle
TOS
de la figure 2 mesure 540.
Calculer l’angle
SOR.
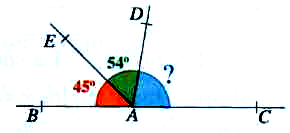
52)
A, B et C sont des points alignés. Calculer l’angle
CAD.
53)
Vrai ou faux ?
-
Si
A=750
et
B=150,
A
et
B
sont des angles supplémentaires. -
Si
A=850
et
B=50,
A
et
B
sont des angles
complémentaires. -
Si
A=1120
et
B=680,
A
et
B
sont des angles
complémentaires.
54) Calculer l’angle marqué d’un « ? »
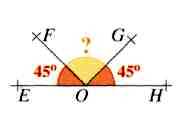a)
b)
c)
55) Reproduire la figure ci-dessous.
-
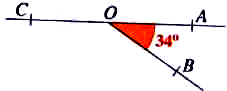
Tracer un point D tel que les angles
AOB
et
COD
soient opposés par le sommet. -
Calculer
COD
et
BOC.
56)
Les angles
A
et
B
sont supplémentaires.
-
Calculer
A
si : a)
B=170 ;
b)
B=580 ;
c)
B
= 790.
-
Calculer
B
si : a)
A=1240 ;
b)
A=1520 ;
c)
A
= 1430.
57)
Les angles
A
et
B
sont complémentaires. Calculer
A
si :
a)
B=170 ;
b)
B=580 ;
c)
B
= 790.
58) Sur la figure suivante, trouver et citer :
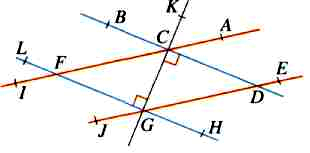a)
deux paires d’angles opposés par le sommet,
b) deux paires d’angles adjacents supplémentaires,
c) deux paires d’angles adjacents complémentaires.
59) Quels sont dans cette liste les couples d’angles complémentaires ? supplémentaires ?
B=1380 ;
A=1250 ;
C=350 ;
D=420 ;
E=550 ;
F=480.
61)
L’angle
C
et l’angle
D
sont adjacents supplémentaires. La mesure de l’angle
C
est les
de
la mesure de l’angle
D.
Quelle est la mesure de chaque angle ?
62)
L’angle
E
et l’angle
F
sont adjacents complémentaires. La mesure de l’angle
E
est les
de
la mesure de l’angle
F.
Quelle est la mesure de chaque angle ?
63) Trouver a dans chaque cas :
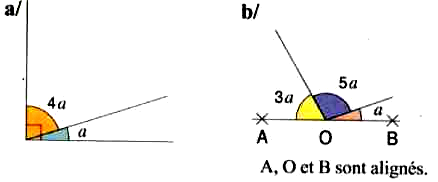
64) Calculer l’angle marqué d’un « ? »
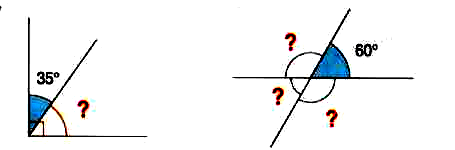a)
b)
65)
XOY
et
YOZ
sont deux angles adjacentes complémentaires. La mesure de
XOY
est le triple de la mesure
YOZ.
Quelle est la mesure de chaque angle ?