2.4 Écriture scientifique
Mots à retenir
une écriture (запись) une notation (запись)
la notation scientifique, l’ écriture scientifique (запись числа в стандартном виде)
grouper (группировать) regrouper (перегруппировать)
compris (содержащийся) soit (пусть будет так)
Remarque
Le verbe « soit » commence souvent un énoncé d’exercice. Il sert à introduire les données de l’exercice. Synonymes : « on donne », « on considère ». On l’utilise aussi pour marquer une équivalence évidente, généralement à la fin d’un raisonnement ou d’un calcul.
Règles
Tout
nombre décimal peut s’écrire comme le produit d’un nombre
compris entre 1 et 10 par une puissance de 10. Ce produit est
appelé la
notation scientifique
du décimal donné :
,
où
,
n est un entier relatif.
Par exemple:
a) 835 000
=
b) 45 =
c)
d)
Méthode : écrire un nombre en notation scientifique
1)
Soit A =
.
Pour trouver la notation scientifique de A, on procède par étapes :
-
; -
; -
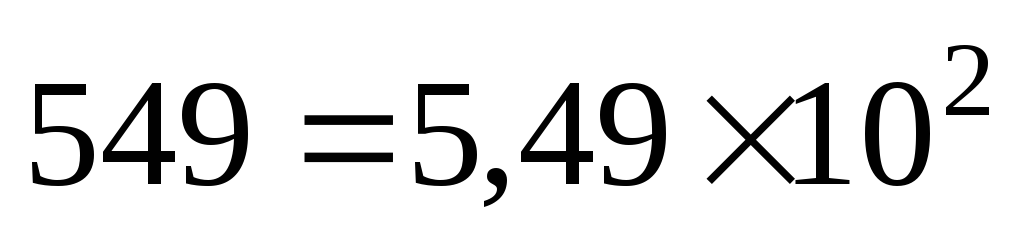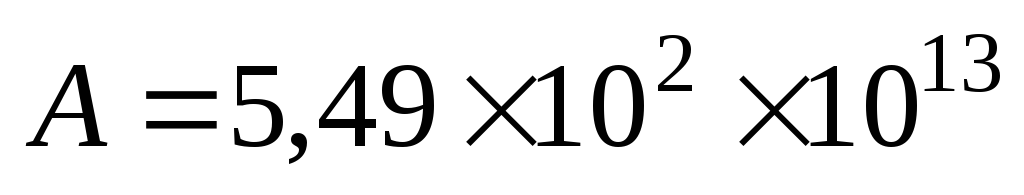on réduit les puissances de 10 :
; -
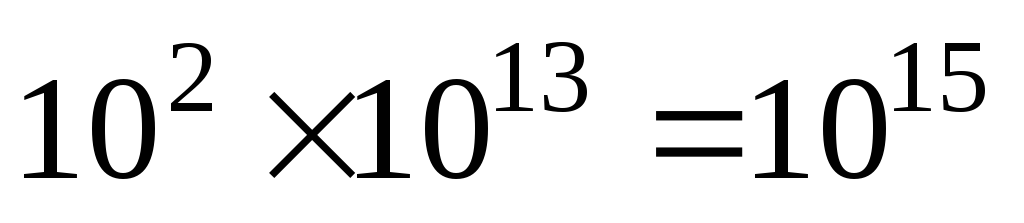donc
.
2)
Soit
.
B est un produit :
-
on peut donc regrouper les facteurs, en particulier les puissances de 10 :
; -
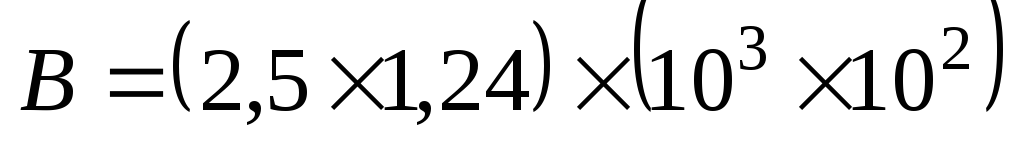on réduit :
et
;
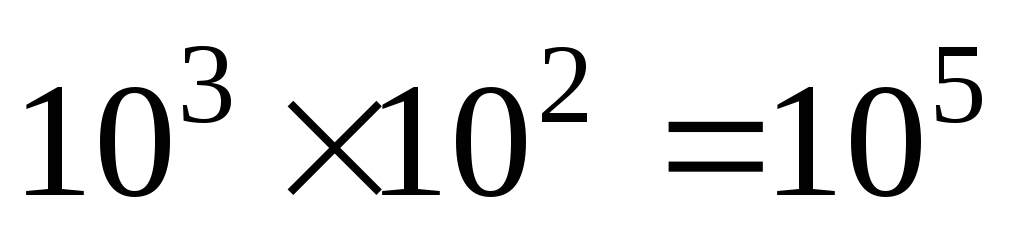alors
; -
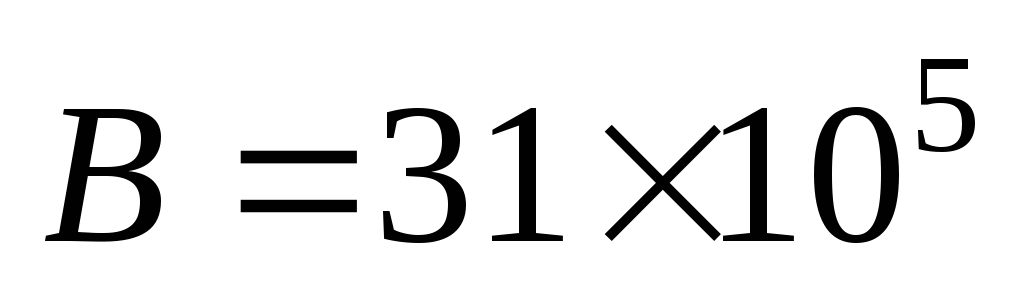on écrit 31 avec notation scientifique :
; -
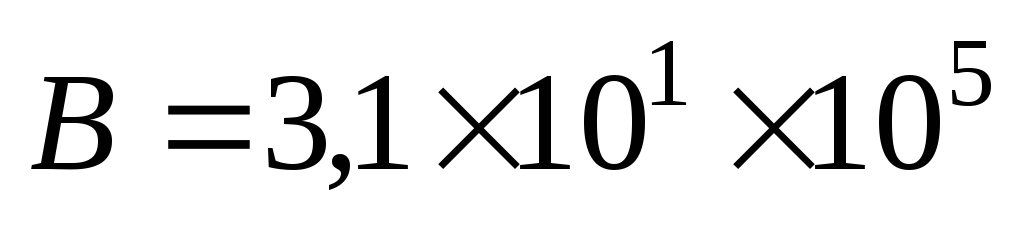donc
.
3)
Soit
.
C est une somme :
-
on applique les régles de priorités :
;
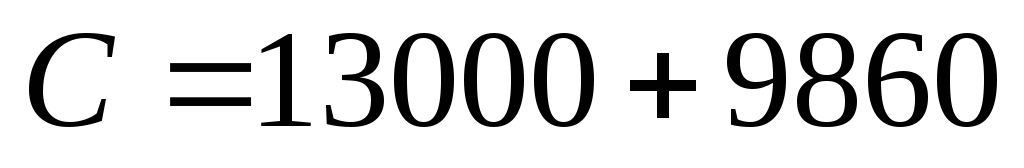alors
; -
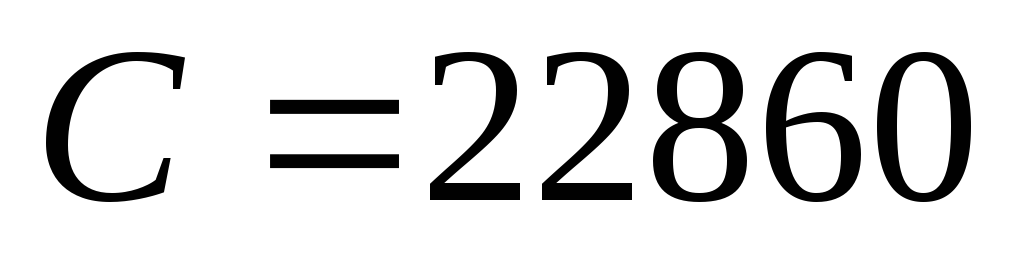on écrit C sous forme scientifique :
.
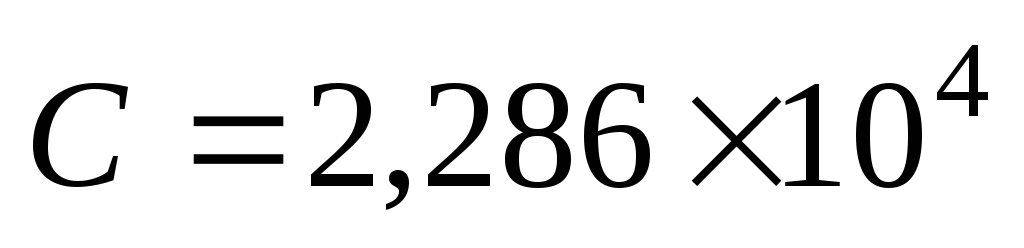4)
Soit
.
D est un quotient :
-
on regroupe les nombres décimaux et des puissances :
; -
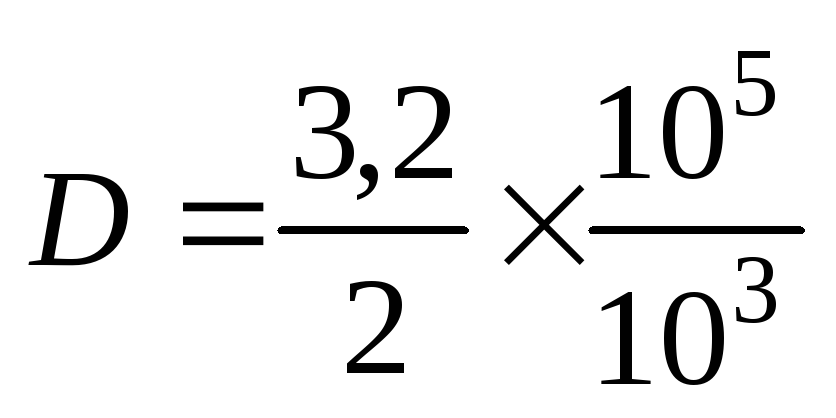on effectue les calculs avec les régles spécifiques aux puissances :
.
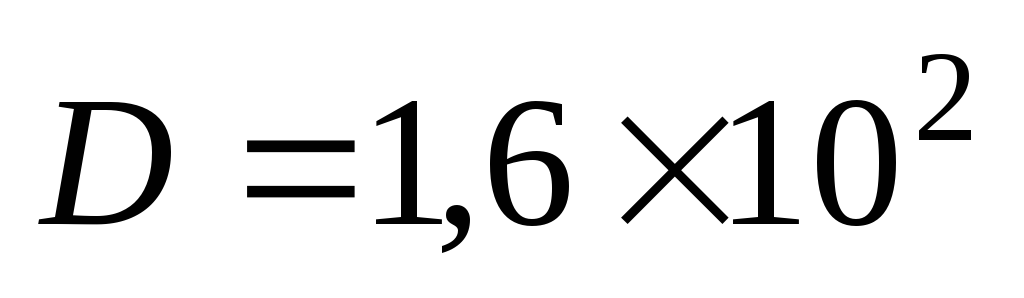Exercices
120) Les expressions ci-dessous sont-elles en notation scientifique ?
a)
b)
c)
d)
121) Donner la notation scientifique des nombres suivents :
a) A=1974 ; b) B=1 394 000 ; c) 75,4 ; d) 5,06.
122) Donner la notation scientifique des nombres suivents :
a)
b)
c)
d)
123) Donner la notation scientifique des nombres suivents :
a)
b)
c)
d)
e)
quinze milliards
124) Calculer et donner la notation scientifique des expressions suivantes :
a)
b)
c)
d)
125) Calculer et donner la notation scientifique des expressions suivantes :
a)
b)
c)
d)
.
126)
On sait que
.
Quelle est l’écriture scientifique des nombres suivants :
127)
On sait que
Écrire sous forme scientifique des nombres suivants :
128) Écrire les nombres suivants sous forme scientifique :
129) Voici les distances en km séparant le Soleil de différentes planétes du système solaire. Écrire ces distances en notation scientifique puis ranger-les de la plus proche du Soleil à la plus éloignée.
Soleil-Jupiter :
Soleil-Vénus :
Soleil-Uranus :
Soleil-Mercure :
Soleil-Mars :
Soleil-Neptune :
Soleil-Terre :
Soleil-Pluton :
Soleil-Saturne :
130)
Calculer a + b ; a - b ; a
b ;
a : b si
et
.
131)
Calculer a + b ; a - b ; a
b ; a : b si
et
.
132)
Calculer pour
et
a) le produit de x et y; b) la somme de x et y; c) le quotient de x par y;
d) la diffèrence entre x et y.
133)
Calculer a + b ; a - b ; a
b ; a : b si
et
.
n est un nombre naturel.
134)
Calculer a + b ; a - b ; a
b ; a : b si
et
.
n est un nombre naturel