2 Вопрос

Понятие о групповой скорости в волноводе.

На практике обычно по волноводам передается сложный сигнал, состоящий из спектра частот. Следовательно, каждая частота, входящая в спектр, будет распространяться с разными скоростями.

Например, АМ-колебания:

Каждая из этих гармоник распространяется со своей скоростью:

Обычно , поэтому может быть разложено в ряд Тейлора по :

- несущая, - огибающая

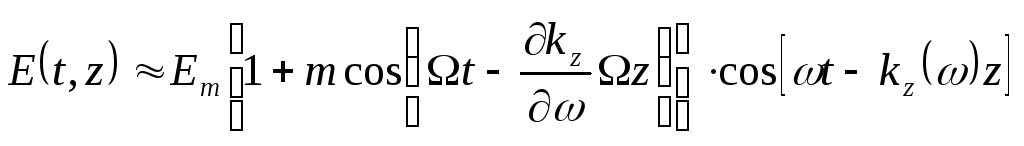
Рассмотрим фазу высокой частоты:

, ,

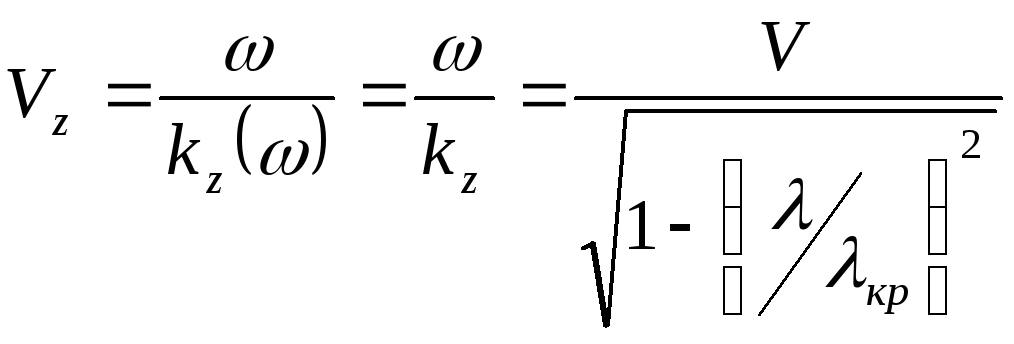
Рассмотрим фазу низкой частоты:

, ,

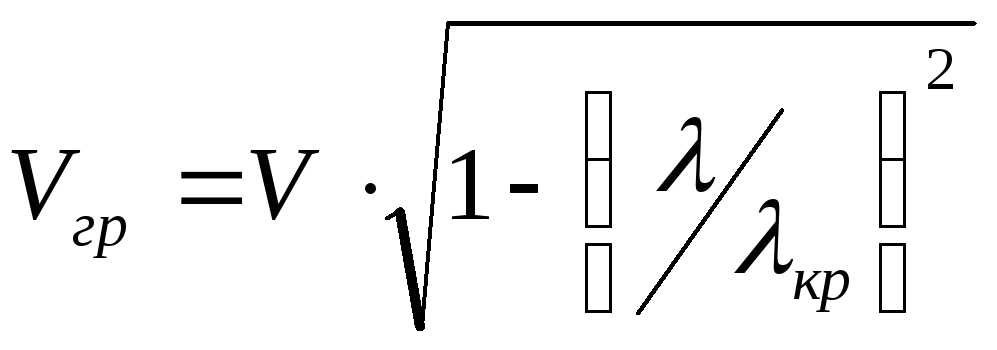, - групповая скорость (скорость несущей и огибающей вместе).

Это выражение верно, когда простейший вариант, в сложных - оно будет неправильно.

Из-за разности скоростей искажается форма выходного сигнала.

Групповая скорость – скорость перемещения энергии.

,

2

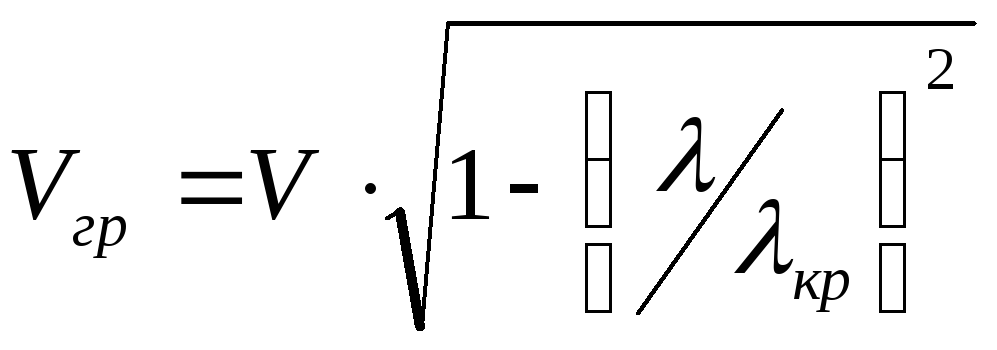
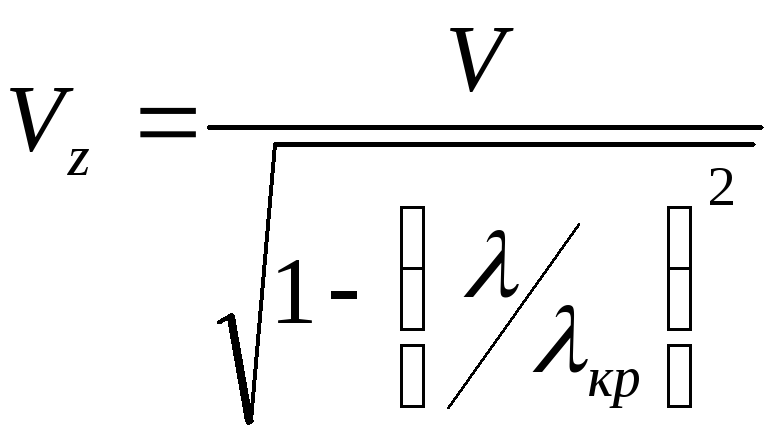
Для пустого волновода:

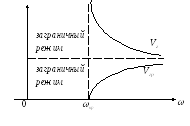
Билет 11 1. Мощность, передаваемая линией передач.

Мощность, проходящая через любую линию передач:

(интегрируем по поперечному сечению).

- среднее значение за период составляющей вектора Умова-Пойтинга по Z

; - волновое сопротивление линии передач

Найдем мощность в прямоугольном волноводе для волны .()

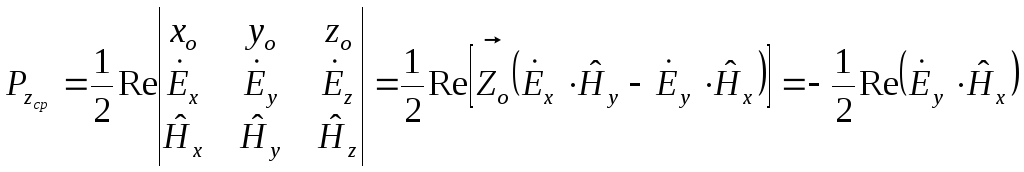
Если подставить и проинтегрировать получим:

, -пар. волновода, ; =>

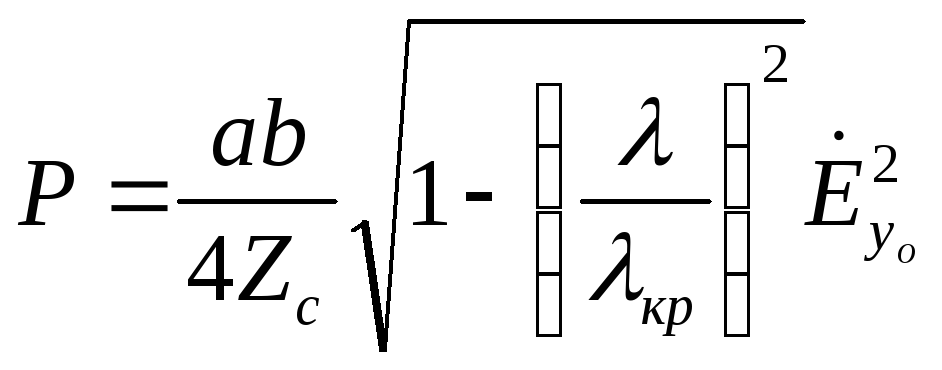
Если в полученной формуле считать, что , , , то получим формулу:

В волноводной технике (и вообще в линиях передач) возникает понятие:

Предельной мощности – максим. мощность, пропускаемая по волноводу без пробоя.

Для волновода, заполненного воздухом при нормальных условиях

Тогда

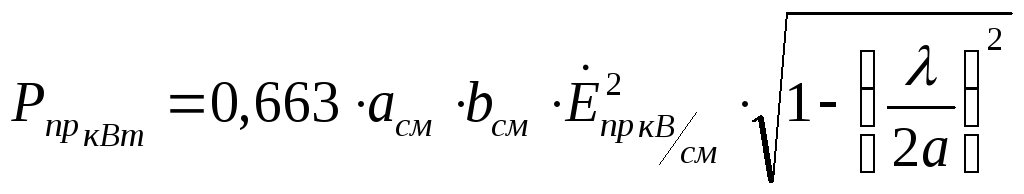
Допустимой мощности – существенно меньше предельной в зависимости от применения изделия.

пример: для прямоугольного волновода , тогда

В ответственных изделиях для повышения пропускаемой мощности иногда волноводы заполняются инертными газами. Другие линии передач имеют более низкую мощность, чем прямоугольные волноводы.

2. Длина волны в волноводе и фазовая скорость.

Коэффициент распространения:

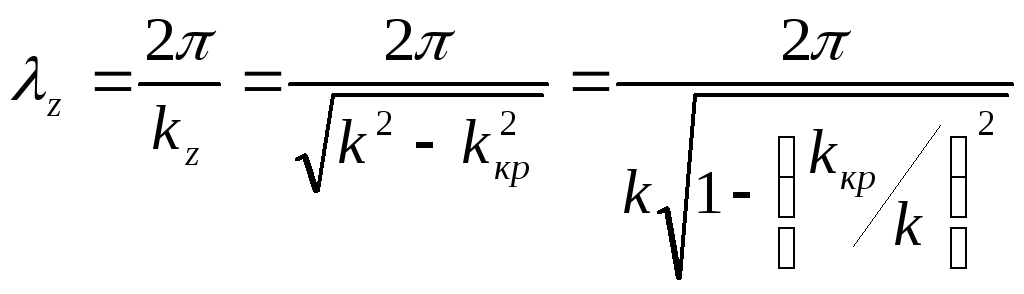
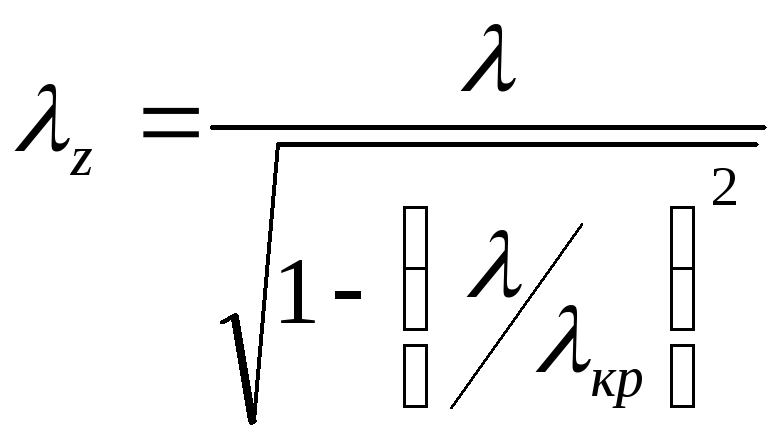
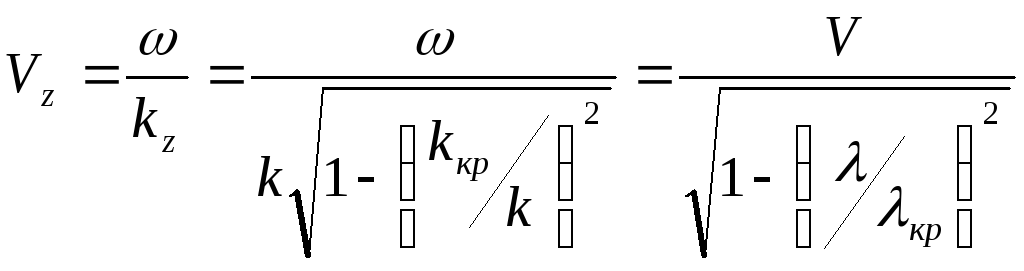
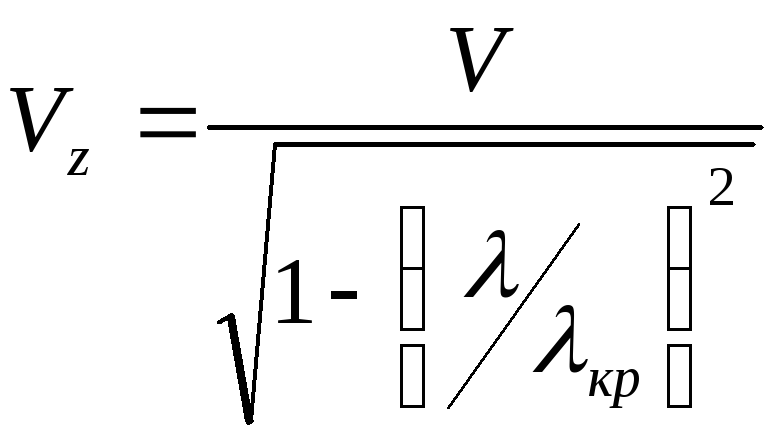
Длина волны в волноводе больше, чем в безграничной среде. Фазовая скорость также больше. Длина волны и фазовая скорость – дисперсионные системы.

Если волновод пустой: ,

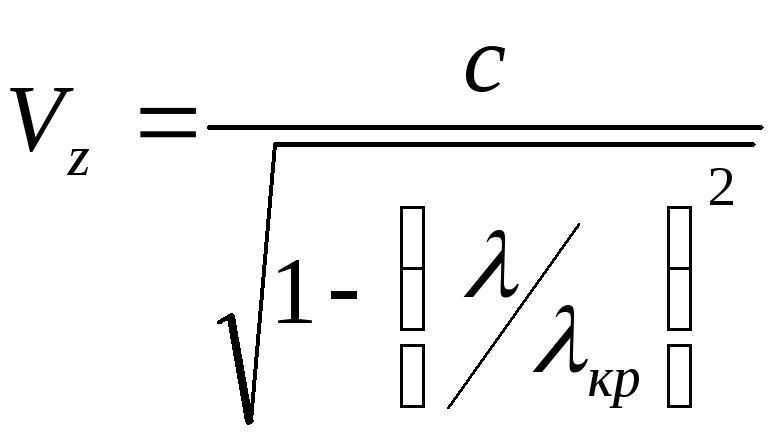
Билет 12 Закон Брюстера

Пусть угол падения i таков, что отраженный луч перпендикулярен преломленному, т.е. r = π/2 - i_Бр. Это условие называют условием Брюстера (см. рисунок ниже), а угол - углом Брюстера - i_Бр.

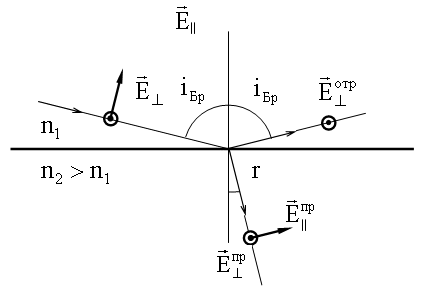
Используя закон преломления

     

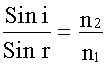
получим формулу, определяющую угол Брюстера:

.

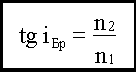При выполнении условия Брюстера i + r = π/2, тогда из формулы Френеля для получим:

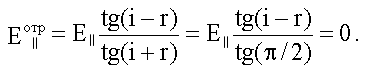
Таким образом, при выполнении условия Брюстера, отраженный свет будет полностью поляризован в плоскости, перпендикулярной плоскости падения.

Это утверждение носит название закона Брюстера

2.Решение краевой (граничной) задачи в прямоугольном волноводе.

Согласно системе (13) решим уравнение:

При граничных условиях: 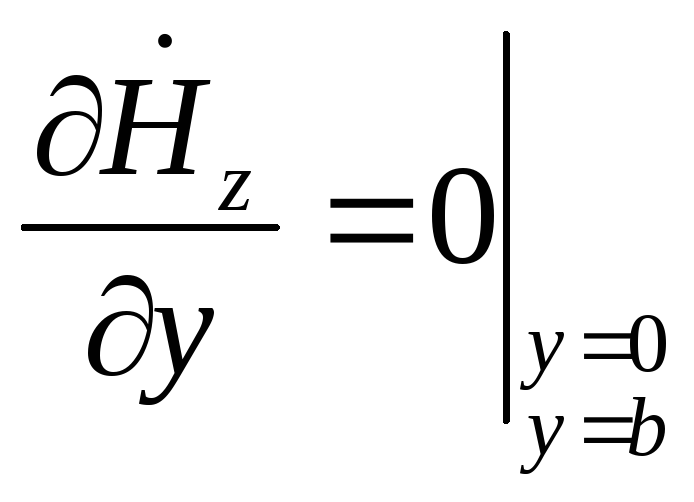и

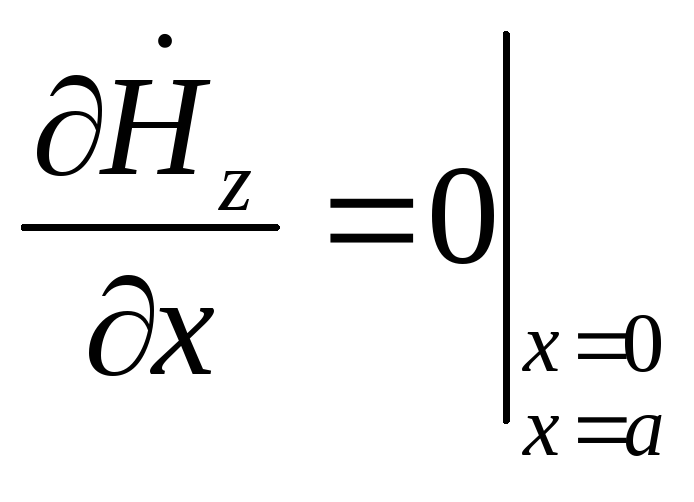
Решать надо двумерное волновое уравнение. Решают ур-ние методом разделения переменных.

подставим в исходное уравнение.

Слева функции только переменной X, справа функция только переменной Y, равенство может выполняться только тогда, когда каждая из частей постоянна.()

постоянные и называют постоянными разделения

Это решение должно удовлетворять граничным условиям:

1. 

,

2. 

,

3. 

,

4. 

,

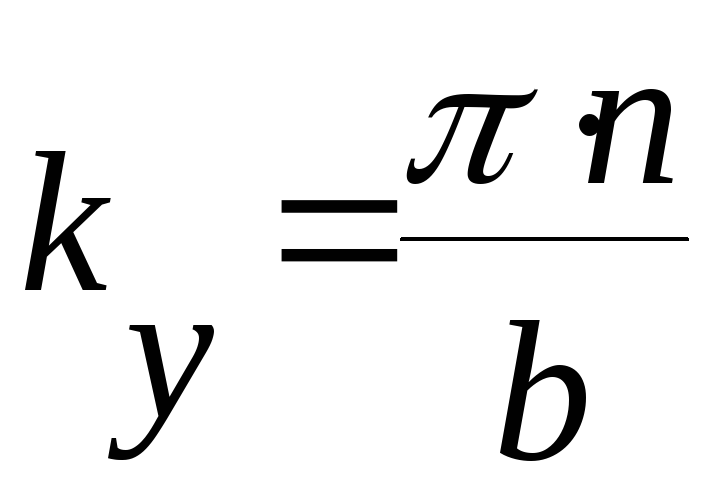
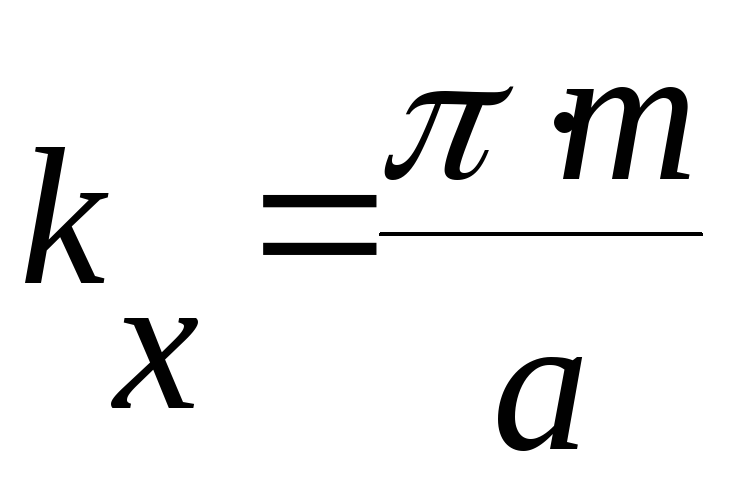
Билет 13 1. Мощность излучения. Сопротивление излучения. КПД элементарного электрического вибратора.

Мощность:

Необходимо интегрировать по поверхности большого радиуса, т. е. по поверхности, проходящей в дальней зоне, т. к. там поле и синфазны и вектор Умова-Пойтинга направлен всегда в сторону распространения энергии

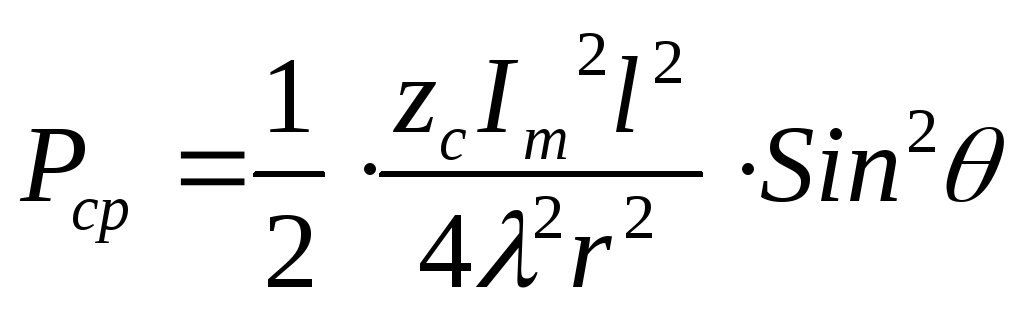
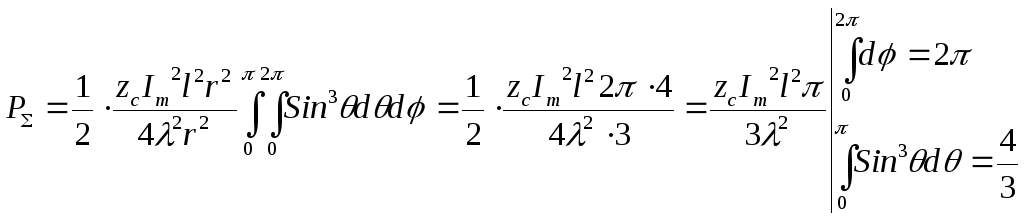
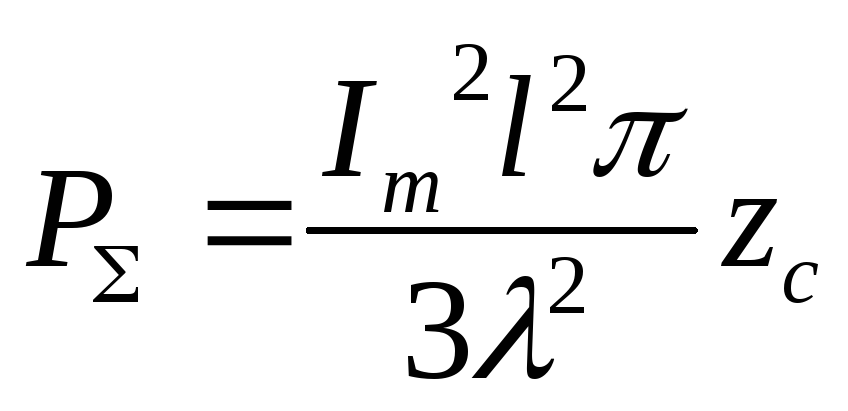, для воздуха (Ом)

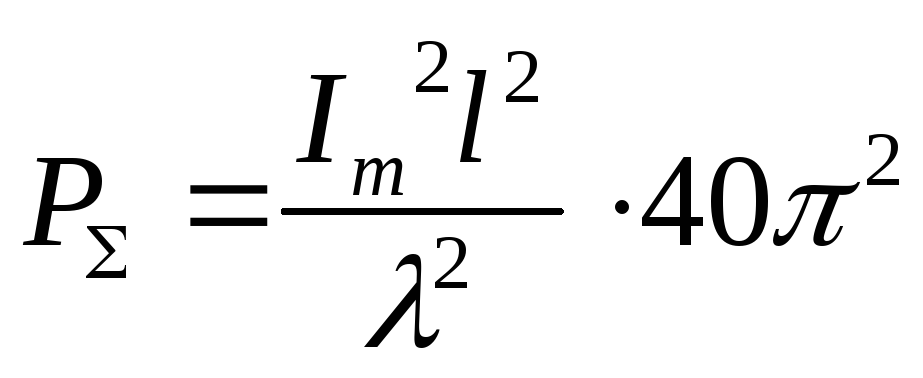, - электрический размер вибратора

Эта мощность выделяется на каком-нибудь сопротивлении (на входе вибратора)

сопротивление излучения (воображаемое сопротивление)

Эта величина является очень важным параметром в теории антенн. Она характеризует излучающую способность всякой антенны (не зависит от величины тока, а определяется целиком электрическими размерами)

При увеличении размера антенны, увеличивается

Это сопротивление является воображаемым, его нет физически, т. к. вся мощность, выделяющаяся на нем, реально рассеивается во всем окружающем пространстве. Оно всегда чисто активно.

мысленно подключено ко входу антенны

Поступающая в антенну мощность выделяется на этом сопротивлении, а также частично затрачивается на потери (за счет конечной проводимости проводов антенны и потерь других устройств (изоляторы))

Отсюда понятие КПД:

полезная, потери